

谐波分析方法提高了精度减少了智能电表的计算开销
描述
作者:Petre Minciunescu, Ph.D. and Gabriel Antonesei
随着智能电表、智能电网和分布式发电的广泛部署,电能质量监测变得越来越重要。电流和电压信号的谐波分析使电表能够表征关键的电能质量指标,包括负载或电源的状态,从而实现预测性维护或系统优化。
谐波的存在是能源供应商和消费者越来越关注的问题,因为过多的谐波电流会导致电力变压器、无功补偿器和中性导体过热,并可能导致保护继电器误跳闸。谐波电压和电流也会干扰在大型谐波发生器附近运行的敏感设备。
为了执行谐波分析,开发人员传统上使用数字信号处理器 (DSP) 来实现某种版本的傅里叶算法或带通滤波。本文介绍了一种新的方法,即自适应实时监控(ARTM),并将其与FFT算法和带通滤波进行了比较。ARTM将出现在ADI公司的下一代能源应用产品中。
基于傅里叶的方法
在电能计量或电能质量监测系统中执行谐波分析时,会同时对相电流和电压进行采样。接下来,对它们进行处理以计算基波和谐波分量的电能质量,包括:有功、无功和视在功率、均方根值、功率因数和谐波失真。快速傅里叶变换 (FFT) 分析立即浮现在脑海中。如图 1 所示,过程如下:
确定基本分量的周期。这种耗时的过程通常是通过对相电压进行低通滤波以隔离基波,然后测量连续过零之间的时间来实现的。确定周期的任何误差都会传播到谐波幅度和相位的误差。
修改采样频率得到2N每个周期的样本数。这意味着使用允许可变采样频率的模数转换器。
获取 2N对应于一个或多个周期的样本。
执行FFT算法。跨多个周期采集的样本提高了计算的准确性,但给DSP带来了更重的负担,并且整体响应更慢。
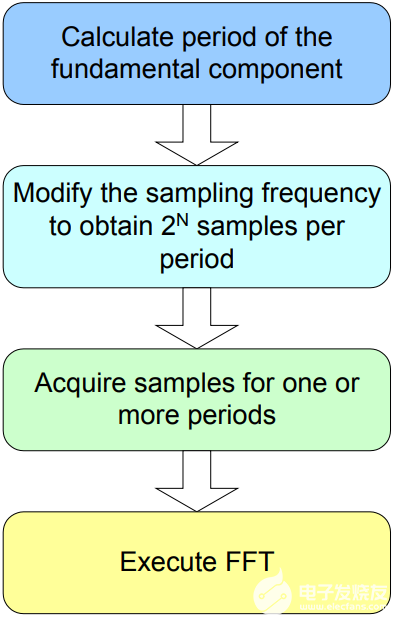
图1.实现FFT算法所需的步骤。
修改采样频率作为基波周期的函数会影响通常在电能表中执行的其他计算。能量计算包括许多滤波器,其系数计算为采样频率的函数。通过采用Goertzel算法,可以避免通过动态调整此类系数来实现整个计量程序。此方法不要求每个周期的样本数等于 2N,从而允许与基波周期无关的恒定采样频率。实现此算法的步骤如下,如图 2 所示:
确定FFT实现中基本组件的周期。
采样频率现在是恒定的,每个周期采集一定数量的样本。
根据每个周期的样本数计算 Goertzel 算法中使用的系数。
执行傅里叶变换。
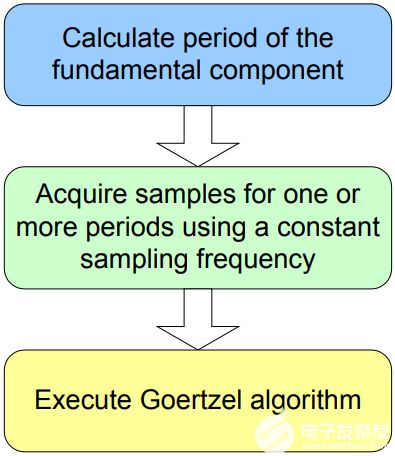
图2.实现Goertzel算法的步骤。
基于带通滤波器的方法
也许最简单的谐波分析方法是使用带通滤波器:获取相电流和电压,并在一个谐波周围应用窄带滤波器。如果并行实施多个滤波器,则可以同时分析多个谐波。实现此方法的步骤如下所示,如图 3 所示:
像以前一样确定基本面的周期。由于在较高谐波下存在错过目标谐波频率的风险,因此需要大幅提高该测量的精度。这意味着必须分配更多时间来过滤连续零交叉之间的时间段。
根据基周期计算滤波系数。
相电流和电压在所需的谐波下滤波,并计算相应的均方根值。这种方法的一个缺点是只保留谐波的幅度,并且丢失任何相位信息。因此,无法计算谐波功率、功率因数和谐波失真。
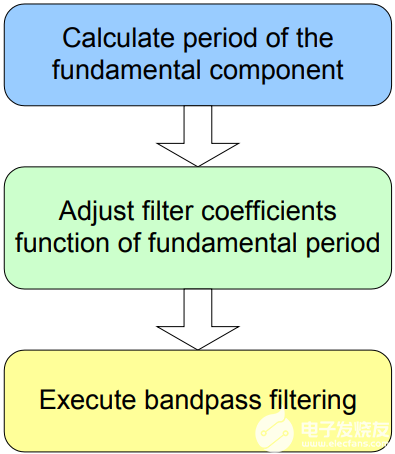
图3.实现带通滤波器的步骤。
自适应实时监控 (ARTM)
由于电网的基频会随着时间的推移而漂移,因此谐波分析仪具有很大的优势,它可以自动跟踪这些频率变化,而无需用户干预。ARTM连续估计基频的可能值,并将其与电压线路上的实际频率进行比较。此比较产生的任何误差都用作增加或减少估计频率值的反馈因子。这基本上是ARTM的自适应元素。
根据估计频率或其整数倍对所选相位的电压和电流执行提取频谱分量的实时程序。此操作将创建一组值,这些值与估计频率或其倍数下存在的能量成比例。进一步的信号处理可以提供基波频率(实际上是谐波)的基波或整数倍的实时功率和均方根值。
对于多相系统,每个相电压都有独立的频率估计器专用于此。因此,即使一相电压下降,用户也可以选择剩余的相之一来估计电网的频率,并将其用于ARTM程序。
整数乘法因子以灵活的方式确定将监控哪个谐波。这样做的好处是将所有DSP计算资源专用于仅监视感兴趣的谐波。相比之下,FFT方法将同时计算频谱多个频率的值,但会消耗更多资源。为了达到相同的性能水平,与所提出的实时方法相比,存储FFT算法使用的样本所需的内存量明显更高。
如果同时监测基本值,监测某个谐波将变得更加强大和重要:这样就可以计算电流和电压均方根分量的谐波失真(HD)比,这个指标有时比绝对值更有意义。事实上,从纯粹的理论DSP的角度来看,这是一种广泛且公认的以标准化方式呈现数据的方法。在进一步的步骤中,对某些谐波指数范围的HD值进行扫描,可以通过将获得的值相加来计算总谐波失真(THD)。
除了频率范围内的幅度响应外,经典且完整的谐波分析仪还应提供有关某些频率下的相位响应的信息。ARTM 根据计算的功率因数提供相位信息,即有功功率与视在功率之比。ARTM 计算对应于基频(称为位移功率因数)和各种谐波频率的功率因数。实时获得这些值作为电能质量的全局指标非常有用,但对于试图实现旨在将功率因数保持在给定边界内的控制环路的系统也是如此。
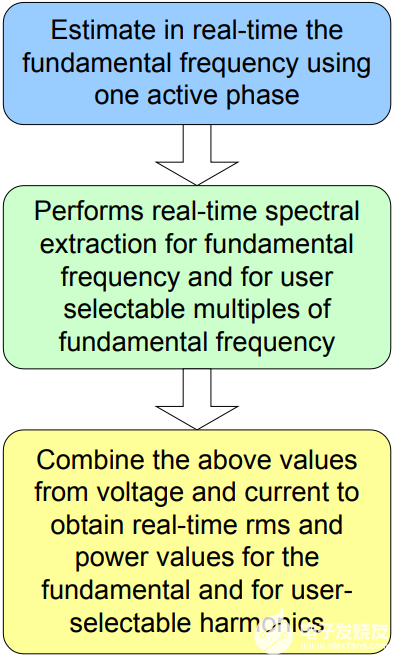
图4.实施自适应实时监控的步骤。
实时计算有功、无功和视在功率的另一个好处是,基波或谐波的能量值可以通过累积获得。这允许用户分析总能耗如何在基波和谐波分量之间分布。
在三相系统中,人们对零线电流的谐波分析和相电流的总和进一步感兴趣,特别是在存在由各种非线性负载产生的三次谐波(三次谐波的奇数倍)的情况下。由于三次谐波的净效应是累加的,中性导体最终可能会承载比设计更多的电流,从而导致过热和可能的火灾。三联体还可能导致三相三角形变压器出现问题,因为循环电流会使绕组过热。能够监测零线电流上的谐波分量以及相电流的总和也有助于指示这些潜在的不平衡问题。
总之,可以说ARTM具有与执行实时监视或控制的系统相关的所有优点。而且,由于 ARTM 将大部分 DSP 资源集中在仅监测目标谐波上,因此可提供更高的效率和更好的性能。
可以对频率进行扫描,以获得谐波频谱的全貌。
表1提供了本文中讨论的各种方法的比较摘要。带通滤波和ARTM可用于实时监测基波和谐波分量。如果电源线的基频发生变化,ARTM方法被证明可以立即以足够的精度做出响应。对于FFT(因为需要样本存储),最终实现占用的内存非常大,而在其它方法的情况下,占用的内存非常小。结果的准确性对于ARTM非常高,对于Goertzel算法和带通滤波器是中等的,对于FFT来说则很低。
| 方法 | 实时监控 | 适应的 | 数字信号处理器内存要求 | 相对精度 | 频谱谐波快照 |
| ARTM | 是的 | 是的 | 小 | 非常高 | 是的 |
| FFT | 不 | 不 | 非常大 | 低 | 是的 |
| Goertzel Algorithm | 不 | 不 | 小 | 中等 | 是的 |
| 带通滤波 | 是的 | 不 | 小 | 中等 | 不 |
审核编辑:郭婷
-
新型谐波分析方法提高了精度减少了智能电表的计算开销2023-01-31 2480
-
新型谐波分析方法提高智能电表精度的技巧精选2019-09-16 2112
-
新型谐波分析方法提高了精度减少了智能仪表的计算开销2019-07-15 1184
-
谐波分析和测量要求,有效抑制谐波伤害!2019-04-28 2960
-
谐波分析计算方法上与前面提到的常规测量有很大的不同2019-01-21 2232
-
功率分析仪是不能同时进行常规测量和谐波分析2019-01-20 2191
-
对于功率分析仪来说,谐波分析是一个重要的功能2019-01-17 3334
-
谐波分析仪WT3000应用实测2018-11-30 2180
-
谐波分析仪WT3000应用实测:测量变频器效率2018-11-26 1840
-
具有谐波分析功能的数字功率计WT3000可进行高精度2018-09-01 2255
-
求基于DSP的谐波分析程序!2015-05-28 3075
-
新型谐波分析方法提高智能电表的精度并降低计算开销2011-11-15 1457
-
CPLD在多功能谐波分析仪设计中的应用2009-10-15 1015
-
什么是谐波分析2008-11-22 4274
全部0条评论

快来发表一下你的评论吧 !

