宽带A/D转换器前端设计注意事项：何时使用双变压器配置

作者：Rob Reeder and Ramya Ramachandran

变压器用于隔离和将信号从单端转换为差分。在高速A/D转换器的前端电路中使用变压器时，一个经常被忽视的因素是它们从来都不是理想的。对于正弦输入信号，变压器引入的任何不平衡都会向ADC的输入提供不完美的正弦波，并导致整体数据转换性能比ADC本来可以提供的性能差。我们在此考虑输入不平衡对ADC性能的影响，并提供电路示例以实现改进的结果。

关于变形金刚

许多制造商提供的型号种类繁多，可能会使变压器选择成为一个令人困惑的过程。供应商在具体规定业绩方面采取的不同方法使挑战更加复杂。它们在指定参数的选择和定义上通常有所不同。

选择变压器驱动特定ADC时需要考虑的一些关键参数是插入损耗、回波损耗、幅度不平衡和相位不平衡。插入损耗是变压器带宽能力的指南。回波损耗也很有用，它允许用户设计终端以匹配变压器在特定频率或频带下的响应，这在使用匝数比大于单位匝数比的变压器时尤其重要。本文将重点介绍幅度和相位不平衡，以及它们如何影响ADC在高带宽应用中的性能。

理论分析

即使带宽额定值很宽，变压器的单端初级和差分次级之间的耦合虽然是线性的，但也会引入幅度和相位不平衡。当应用于转换器（或其他差分输入器件）时，这些不平衡会加剧转换（或处理）信号的偶数阶失真。虽然在低频时通常可以忽略不计，但高速转换器中增加的失真在大约100 MHz时变得非常明显。我们首先来看看差分输入信号的幅度和相位不平衡，特别是二次谐波失真，如何影响ADC的性能。

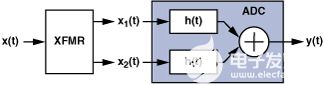
图1.使用变压器的ADC前端的简化框图。

考虑变压器的输入 x（t）。它被转换为一对信号，x1(t） 和 x2(如果 x（t） 为正弦，则差分输出信号 x1(t） 和 x2(t），的形式为

 

(1)

 

ADC建模为对称三阶传递函数：

 

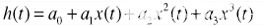(2)

 

然后

 

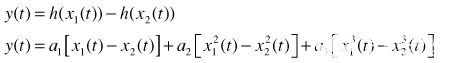
(3)

 

理想情况 - 无不平衡

当 x1(t） 和 x2(t） 是完全平衡的，它们具有相同的星等 （k1 = k2 = k） 并且正好是 180° 异相 （φ = 0°）。因为

 

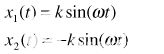(4)

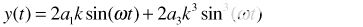(5)

 

将三角恒等式应用于幂并收集类似频率的项，

 

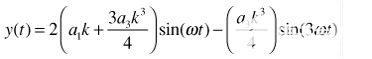
(6)

 

这是差分电路的常见结果：偶谐波抵消理想信号，而奇次谐波则不会。

量级不平衡

现在假设两个输入信号有一个幅度不平衡，但没有相位不平衡。在这种情况下，k1≠ k2，φ = 0。

 

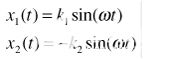(7)

 

代入等式3中的等式7，并再次应用三角幂恒等式，

 

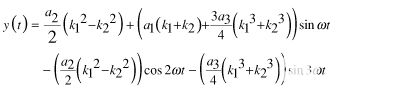
(8)

 

从公式8可以看出，在这种情况下，二次谐波与幅度项的平方差成正比，k1和 k2即。

 

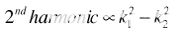(9)

 

相位不平衡

现在假设两个输入信号之间存在相位不平衡，没有幅度不平衡。

然后，k1 = k2，φ ≠ 0。

 

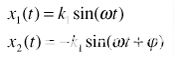(10)

 

代入等式3中的等式10并简化，

 

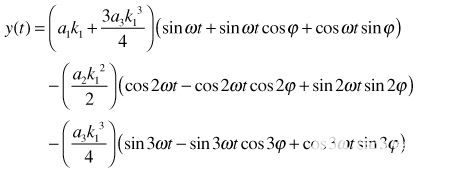
(11)

 

从公式11可以看出，二次谐波幅度与幅度项k的平方成正比。

 

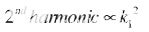(12)

 

观察

比较公式9和公式12表明，二次谐波幅值受相位不平衡的影响比幅度不平衡的影响更严重。对于相位不平衡，二次谐波与k的平方成正比1，而对于幅度不平衡，二次谐波与k的平方差成正比1和 k2.由于 k1和 k2大致相等，这个差异很小。

为了测试这些计算的有效性，为上述模型编写了MATLAB代码，以量化和说明幅度和相位不平衡对具有变压器输入的高性能ADC谐波失真的影响（附录A）。该模型包括加性白高斯噪声。

系数，一个我，用于 MATLAB 型号的是一款高性能 16 位、125 MSPS ADC AD9445。AD9445采用图2所示前端配置，用于生成图3所示FFT，系数由此推导。

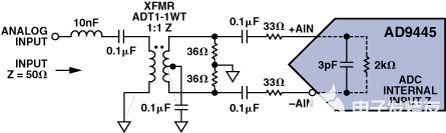
图2.带变压器的AD9445前端配置

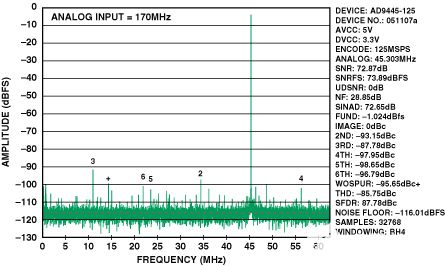
图3.AD9445的典型FFT，125 MSPS，IF = 170 MHz。

这里的本底噪声、二次谐波和三次谐波反映了转换器和前端电路的复合性能。转换器失真系数（a2和3）和噪声是使用这些测量结果计算的，并结合标准1：1阻抗比变压器指定的170 MHz时0.0607 dB的幅度不平衡和148 MHz时的相位不平衡。

这些系数在公式8和公式11中用于计算y（t），而幅度和相位不平衡分别在0 V至1 V和0度至50度范围内变化（典型变压器的不平衡范围在1 MHz至1000 MHz范围内），并观察对二次谐波的影响。仿真结果如图 4 和图 5 所示。

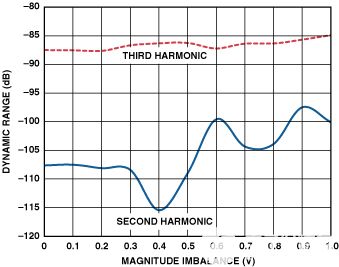
图4.仅绘制谐波与幅度不平衡的关系。

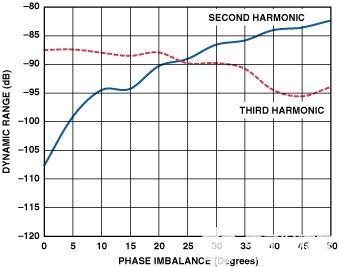
图5.仅绘制谐波与相位不平衡的关系图。

图4和图5显示（a）三次谐波对幅度和相位不平衡相对不敏感，（b）二次谐波在相位不平衡时比在幅度不平衡时恶化得更快。因此，为了从ADC获得更好的性能，需要具有改善相位不平衡的变压器配置。图6和图7显示了两种可行的配置，第一种涉及双巴伦，第二种涉及双变压器。

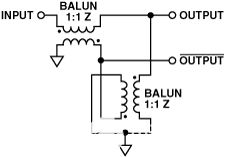
图6.双巴伦配置。

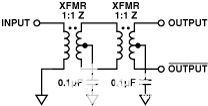
图7.双变压器配置。

在专门设计的表征板上使用矢量网络分析仪比较了这些配置的不平衡。图8和图9比较了这些配置与单个变压器的幅度和相位不平衡。

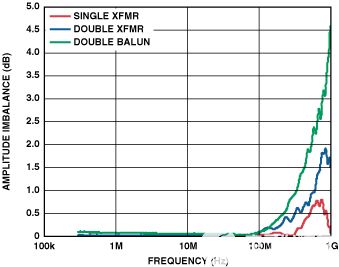
图8.从 1 MHz 到 1000 MHz 的幅度不平衡。

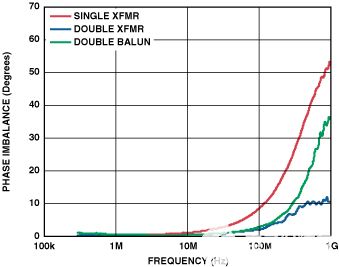
图9.相位不平衡从1 MHz到1000 MHz。

上图清楚地表明，双构型具有更好的相位不平衡，但代价是幅度不平衡略有下降。因此，使用上述分析的结果，似乎可以使用双变压器配置来实现更好的性能。使用单变压器输入（图10）和双巴伦输入（图11）的AD9445的FFT图表明情况确实如此;使用 300MHz IF 信号时，SFDR 提高了 +10 dB。

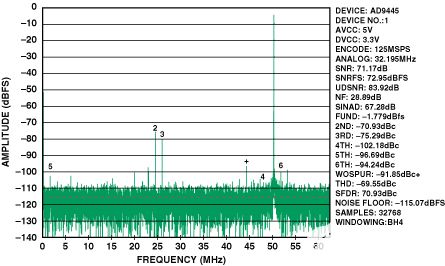
图 10.单变压器输入，AD9445的FFT。125 MSPS，IF = 300 MHz。

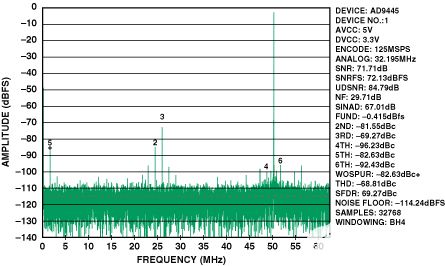
图 11.双巴伦输入，AD9445的FFT。125 MSPS，IF = 300 MHz。

这是否意味着要获得良好的性能，必须在ADC前端耦合两个变压器或两个巴伦？不一定。分析表明，必须使用相位不平衡很小的变压器。在以下示例（图12和图13）中，使用两个不同的单变压器驱动具有170 MHz IF信号的AD9238。这些示例表明，当ADC由改善高频相位不平衡的变压器驱动时，二次谐波改善了29 dB。

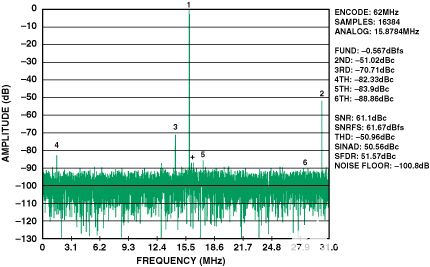
图 12.单变压器输入，AD9238的FFT。62 MSPS，IF = 170 MHz @ –0.5 dBFS，二次谐波 = –51.02 dBc。

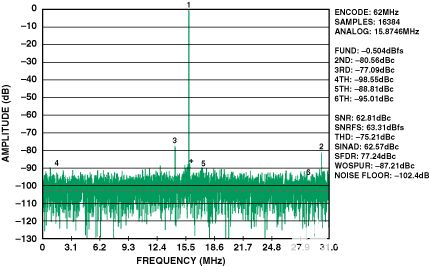
图 13.单变压器输入，AD9238的FFT。62 MSPS，IF = 170 MHz @ –0.5 dBFS，二次谐波 = –80.56 dBc。

结论

当变压器用作具有高中频输入（>100 MHz）的过程（如A/D转换、D/A转换和放大）的前端时，变压器的相位不平衡会加剧二次谐波失真。然而，通过使用一对变压器或巴伦，可以很容易地实现显着的改进，但代价是额外的变压器和额外的印刷电路板空间。

如果设计带宽较小且选择合适的变压器，单变压器设计可以实现足够的性能。但是，它们确实需要有限的带宽匹配，并且它们可能很昂贵或物理很大。

无论哪种情况，为任何给定应用选择最佳变压器都需要详细了解变压器的规格。相位不平衡对于高中频输入（>100 MHz）尤为重要。即使数据手册中未指定，大多数变压器制造商也会根据要求提供相位不平衡信息。网络分析仪可用于测量变压器的不平衡作为检查，或者如果信息不容易获得。

审核编辑：郭婷