

将放大器建模为模拟滤波器可提高SPICE仿真速度
描述
放大器的仿真模型通常使用电阻器、电容器、晶体管、二极管、相关和独立源以及其他模拟元件来实现。另一种方法是使用放大器行为的二阶近似(拉普拉斯变换),加快仿真速度并将仿真代码减少到三行。
然而,对于高带宽放大器,使用s域传递函数的时域仿真可能非常慢,因为仿真器必须首先计算逆变换,然后将其与输入信号卷积。带宽越高,确定时域函数所需的采样频率就越高。这导致卷积计算越来越困难,减慢了时域仿真的速度。
本文提出了进一步的改进,将二阶近似合成为模拟滤波器而不是s域传递函数,以提供更快的时域仿真,特别是对于更高带宽的放大器。
二阶传递函数
二阶传递函数可以使用Sallen-Key滤波器拓扑实现,该拓扑需要两个电阻、两个电容器和一个用于放大器仿真模型的电压控制电流源;或多反馈 (MFB) 滤波器拓扑,需要三个电阻、两个电容器和一个压控电流源。两种拓扑应提供相同的结果,但Sallen-Key拓扑设计更简单,而MFB拓扑具有更好的高频响应,并且可能更适合可编程增益放大器,因为它更容易切换不同的电阻值。
我们可以使用以下二阶近似标准形式对放大器的频率和瞬态响应进行建模,从而开始该过程:
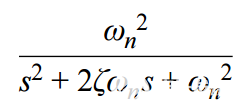
向Sallen-Key的转换和多反馈拓扑如图1所示。
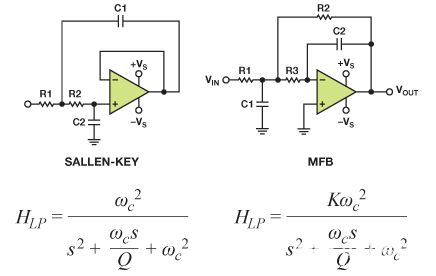
图1 .筛选器拓扑。
放大器的固有无阻尼频率,ωn,等于滤波器的转折频率,ωc,放大器的阻尼比ζ等于滤波器品质因数Q的倒数的1/2倍。对于双极点滤波器,Q 表示极点与 j ω 轴的径向距离,Q 值越高表示极点更接近 jω 轴。使用放大器时,阻尼比越大,峰值越低。这些关系可作为s域(s = jω)传递函数和模拟滤波器电路之间的有用等价。
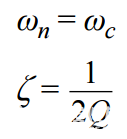
设计示例:增益为5的放大器
该设计包括三个主要步骤:首先,测量放大器的过冲(Mp) 和建立时间 (ts).其次,使用这些测量值计算放大器传递函数的二阶近似值。第三,将传递函数转换为模拟滤波器拓扑,以产生放大器的SPICE模型。
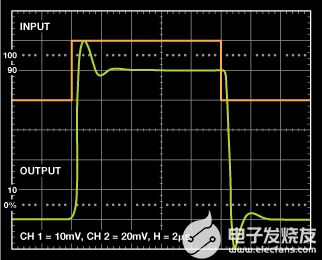
图2.增益为5的放大器。
例如,增益为5的放大器将使用Sallen-Key和MFB拓扑进行仿真。从图2中,过冲(Mp) 约为 22%,2% 的建立时间约为 2.18 μs。阻尼比ζ计算公式为:
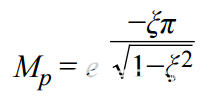
重新排列术语以求解ζ给出
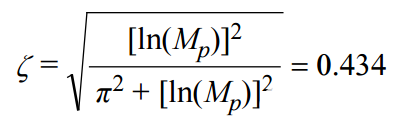
接下来,使用建立时间计算固有无阻尼频率(以弧度/秒为单位)。
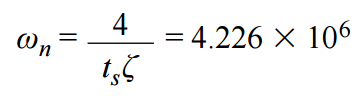
对于步进输入,s2传递函数分母中的 s 项(以弧度/秒为单位)计算公式为
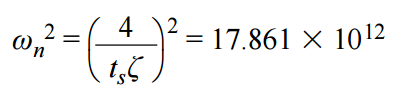
和
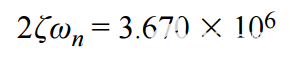
然后,单位增益传递函数变为
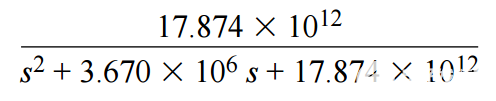
增益为5的放大器的最终传递函数通过将阶跃函数乘以5得到:
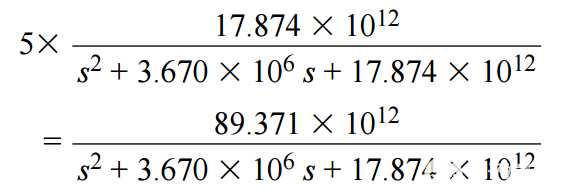
以下网表模拟增益为5的放大器传递函数的拉普拉斯变换。在转换为滤波器拓扑之前,最好运行仿真来验证拉普拉斯变换,通过增大或减小建立时间来根据需要调整带宽。
GAIN_OF_5传递函数***
.SUBCKT SECOND_ORDER +输入 – 输出
E1 OUT 0 LAPLACE {V(+IN) – V(–IN)} = {89.371E12 / (S^2 + 3.670E6*S + 17.874E12)}
.结束
图3显示了时域中的仿真结果。图4显示了频域中的结果。
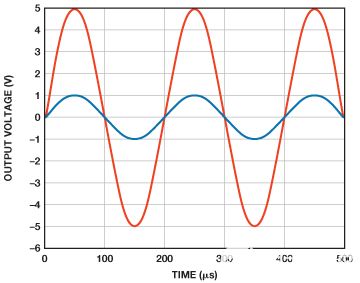
图3.增益为5的放大器:时域仿真结果。
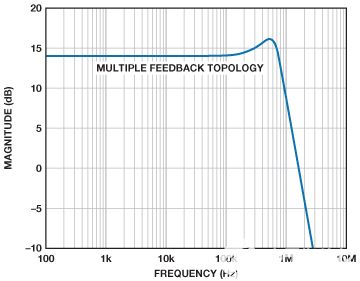
图4.增益为5的放大器:频域仿真结果。
脉冲响应的峰值使得在改变建立时间以修改带宽的同时,易于保持恒定的阻尼比。这改变了复共轭极对相对于实轴的角度,其量等于阻尼比的反余弦,如图5所示。减少建立时间会增加带宽;增加建立时间会降低带宽。只要阻尼比保持恒定,并且仅对建立时间进行调整,峰值和增益就不会受到影响,如图6所示。
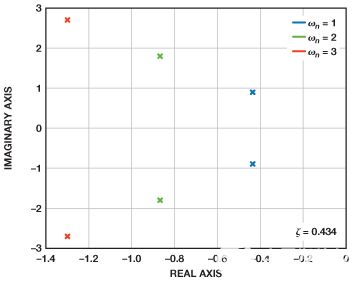
图5.增益为 5 传递函数的复共轭极对。
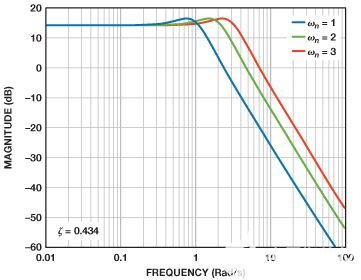
图6.通过建立时间调整实现带宽。
一旦传递函数与实际放大器的特性相匹配,就可以将其转换为滤波器拓扑结构。此示例将同时使用 Sallen-Key 和 MFB 拓扑。
首先,使用单位增益Sallen-Key拓扑的规范形式将传递函数转换为电阻和电容值。
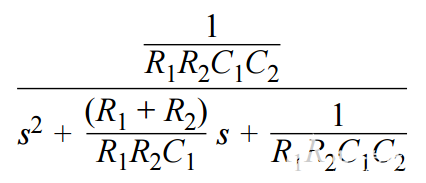
从 s 项来看,C1可以从以下位置找到
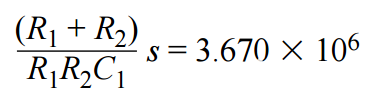
为R选择方便的电阻值,例如10 kΩ1和 R2,并计算 C1.
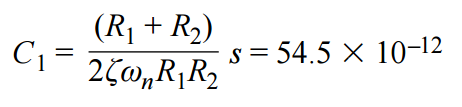
使用转角频率的关系求解 C2.
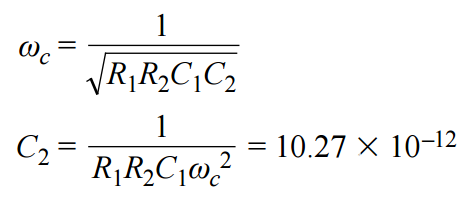
所得网表如下,Sallen-Key电路如图7所示。E1将阶跃函数相乘,得到增益5。Ro 提供 2 Ω的输出阻抗。G1是增益为120 dB的VCCS。E2是差分输入模块。频率与增益仿真与使用拉普拉斯变换的仿真相同。
SUBCKT SALLEN_KEY +IN –IN OUT
R1 1 4 10E3
R2 5 1 10E3
C2 5 0 10.27E–12
C1 2 1 54.5E–12
G1 0 2 5 2 1E6
E2 4 0 +IN –IN 1
E1 3 0 2 0 5
RO OUT 3 2
.END
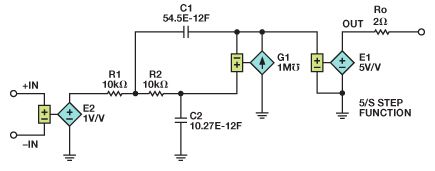
图7.使用Sallen-Key滤波器的增益为5放大器的仿真电路。
接下来,使用MFB拓扑的标准形式将传递函数转换为电阻和电容值。
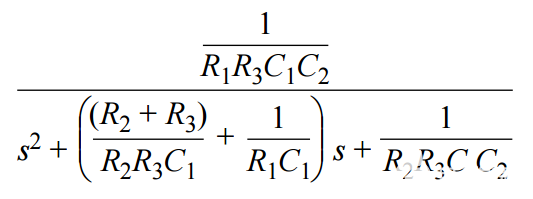
通过计算 R 开始转换2.为此,可以用这种更通用的形式重述传递函数
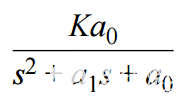
集合 C1= 10 nF。接下来,选择 C2使得根基下的数量为正。为方便起见,C2被选为 10 pF。替换 C 的已知值2= 10 pF, a1= 3.67E6,K = 5,和 a0= 17.86E12 给出 R 的值2:
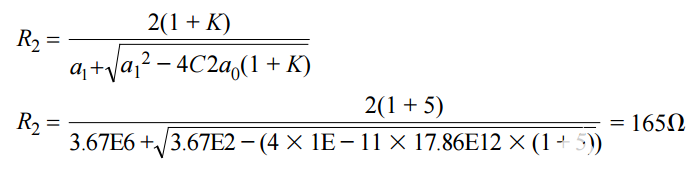
R1可以很容易地找到为 R2/K = R2/5 = 33。从标准多项式系数求解 R3.将已知值替换为0, R2和 C2给
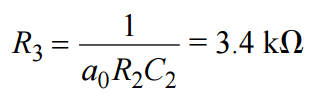
最后,为了验证组件比是否正确,C1将已知值替换为0, R2, R3、增益 K 和 C2(来自 s 项)。
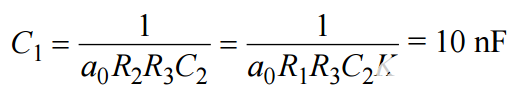
求解分量值后,请代入方程以验证多项式系数在数学上是否正确。电子表格计算器是一种简单的方法。显示的组件值提供了用于最终 SPICE 模型的实用值。在实践中,确保最小电容值不低于10 pF。
增益为5的放大器的网表如下,模型如图8所示。G1 是一款 VCCS(压控电流源),开环增益为 120 dB。请注意,元件数量远低于晶体管、电容器、二极管和相关源所需的元件数量。
.SUBCKT MFB +IN –IN OUT
***VCCS – 120 dB OPEN_LOOP_GAIN***
G1 0 7 0 6 1E6
R1 4 3 330
R3 6 4 34K
C2 7 6 1P
C1 0 4 1N
R2 7 4 1.65K
E2 3 0 +IN –IN 1
E1 9 0 7 0 –1
***OUTPUT_IMPEDANCE RO = 2 Ω***
RO OUT 9 2
.END
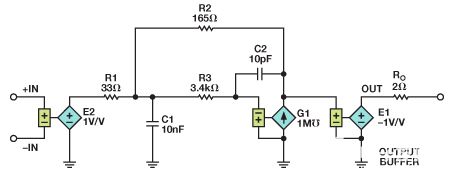
图8.使用MFB滤波器的增益为5的放大器仿真电路。
设计示例:增益为10的放大器
第二个示例是,考虑增益为10的放大器的脉冲响应,无过冲,如图9所示。建立时间约为7 μs。由于没有过冲,脉冲响应可以近似为临界阻尼,ζ ≈0.935(Mp= 0.025%)。
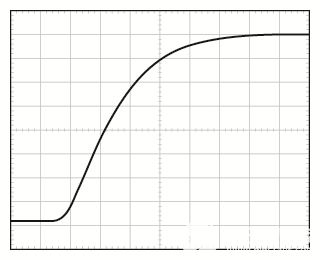
图9.增益为10的放大器,无过冲。
由于没有过冲,可以方便地保持恒定的建立时间并调整阻尼比以模拟正确的带宽和峰值。图10显示了磁极如何随着阻尼比的变化而移动,同时保持恒定的建立时间。图11显示了频率响应的变化。
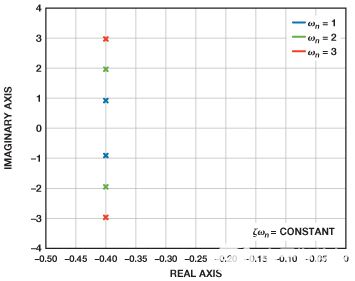
图 10.具有恒定设置时间的不同阻尼比的极点位置。
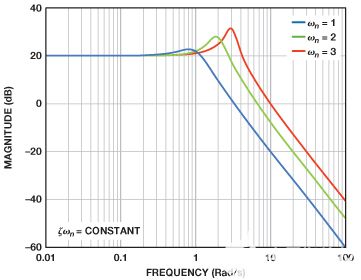
图 11.具有恒定设置时间的不同阻尼比的频率响应。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT PREAMPLIFIER_GAIN_10 +IN –IN OUT
E1 OUT 0 LAPLACE {V(+IN)–V(–IN)} = {3.734E12 / (S^2 + 1.143E6*S + 373.379E9)}
.END
要查找单位增益Sallen-Key拓扑的电阻和电容值,请选择R1 = R2= 10 kΩ 和以前一样。使用增益为5的放大器示例中相同的方法计算电容值:
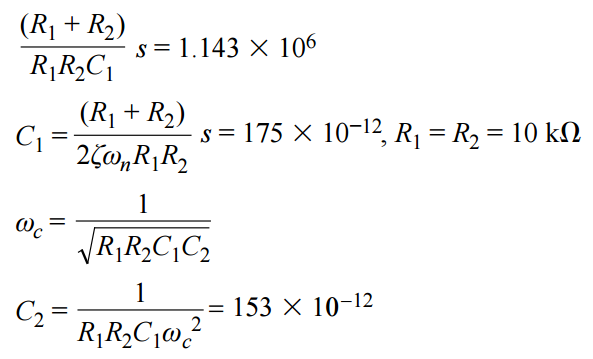
网表如下,Sallen-Key仿真电路模型如图12所示。增益为10的模块E2与2 Ω输出阻抗一起放置在输出级。E2 将单位增益传递函数乘以 10。拉普拉斯网表和萨伦基网表都产生了相同的模拟,如图13所示。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT AMPLIFIER_GAIN_10_SALLEN_KEY +IN –IN OUT
R1 1 4 10E3
R2 5 1 10E3
C2 5 0 153E–12
C1 2 1 175E–12
G1 0 2 5 2 1E6
E2 4 0 +IN –IN 10
E1 3 0 2 0 1
RO OUT 3 2
.END
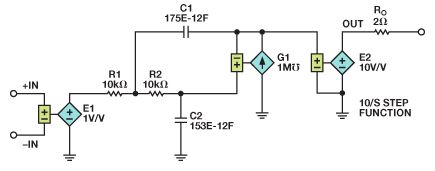
图 12.使用Sallen-Key滤波器的增益为10的放大器仿真电路。
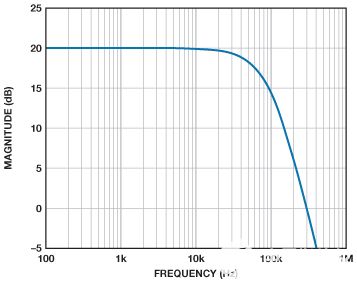
图 13.使用Sallen-Key滤波器对增益为10的放大器进行频域仿真。
可以使用 MFB 拓扑完成类似的推导。网表如下,仿真模型如图14所示。
***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***
.SUBCKT 8208_MFB +IN –IN OUT
***G1 = VCCS WITH 120 dB OPEN_LOOP_GAIN***
G1 0 7 0 6 1E6
R1 4 3 994.7
R2 7 4 9.95K
R3 6 4 26.93K
C1 0 4 1N
C2 7 6 10P
EIN_STAGE 3 0 +IN –IN 1
***E2 = OUTPUT BUFFER***
E2 9 0 7 0 1
***OUTPUT RESISTANCE = 2 Ω***
RO OUT 9 2
.END
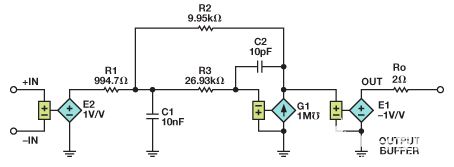
图 14.使用MFB滤波器的增益为10的放大器的仿真电路。
结论
与s域(拉普拉斯变换)传递函数相比,使用模拟组件构建的SPICE模型将为更高带宽的放大器提供更快的时域仿真。Sallen-Key 和 MFB 低通滤波器拓扑提供了一种将 s 域传递函数转换为电阻器、电容器和压控电流源的方法。
MFB 拓扑的非理想操作由 C 导致1和 C2相对于电阻R的阻抗,在高频下表现为短路1, R2和 R3.类似地,Sallen-Key 拓扑的非理想操作由 C1和 C2相对于电阻R的阻抗,在高频下表现为短路1和 R2.两种拓扑的比较如图 15 所示。
CMRR、PSRR、失调电压、电源电流、频谱噪声、输入/输出限制和其他参数常用的现有电路可以与模型组合,如图16所示。
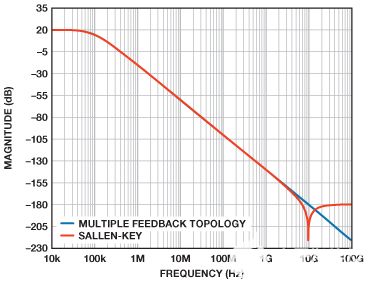
图 15.萨伦基和MFB拓扑的波特图。
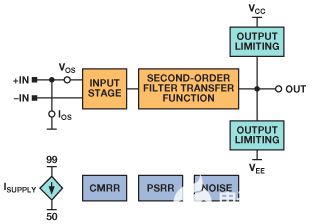
图 16.完整的SPICE放大器模型,包括误差项。
审核编辑:郭婷
-
求助:如何提高modelsim仿真速度?2016-04-16 5858
-
对仪表放大器输入端低通滤波器的匹配和调节2018-09-19 10511
-
模拟滤波器向导设计工具为滤波器选择正确的放大器2018-10-26 3601
-
有源模拟滤波器设计参数有什么?2019-08-20 3342
-
如何将放大器建模为模拟滤波器,从而提高SPICE仿真速度?2019-12-01 2757
-
如何提高MPLAB X仿真速度?2020-03-27 2196
-
带可调滤波器的音频放大器2009-09-08 1038
-
运算放大器构成的带通滤波器2009-12-07 7694
-
Spice仿真器:仿真速度和容量的提升2010-01-23 4202
-
如何使用模拟滤波器注入噪2010-03-23 1060
-
放大器建模为模拟滤波器可提高SPICE仿真速度2016-01-07 667
-
放大器仿真模型可提高SPICE仿真速度2019-04-09 4962
-
如何将单极点滤波器与运算放大器配合使用2019-07-09 3511
-
如何设计有源滤波器?有源滤波器如何选型?2023-11-07 2440
-
GNSS 低噪声放大器前端模块,集成前滤波器和后滤波器 skyworksinc2025-06-06 137
全部0条评论

快来发表一下你的评论吧 !

