

AI是干什么的?机器学习的基础流程和理论基础
人工智能
描述
大家对AI抱有很高热情,也有很多想象,但没法比较准确地概括出AI,并做出一些判断。以下知识可能是个很好的开始,不需要太多基础,最多是高中数学就可以,只需要耐心地花上15-20分钟,并跟着一起思考,相信对您加深对AI的理解会有一些帮助。 那么,我们开始:
机器学习主要价值就是学习一个经验E,根据这个学习到的经验E去执行一个任务T,目标是优化执行任务T的表现P。 比如:在银行,根据数据,AI学习客户表现和客户信用之间的关系,这个关系是经验E;然后为每个客户实时计算更准确的信用卡额度,这个是任务T;目标P是在一定风险承担范围内,增加银行信用卡收入。(因为之前一刀切的额度变更准则,远远不如AI指定的精细额度有效率。) 好了,了解了AI是干什么的,那AI是怎么干呢?
机器学习的基础流程
具体流程如下图,请大家明晰,这七步是在干什么,以什么逻辑和时间轴。后续的介绍将聚焦在其中一两个步骤。但我们经常混淆,比如混淆AI训练和AI执行任务。
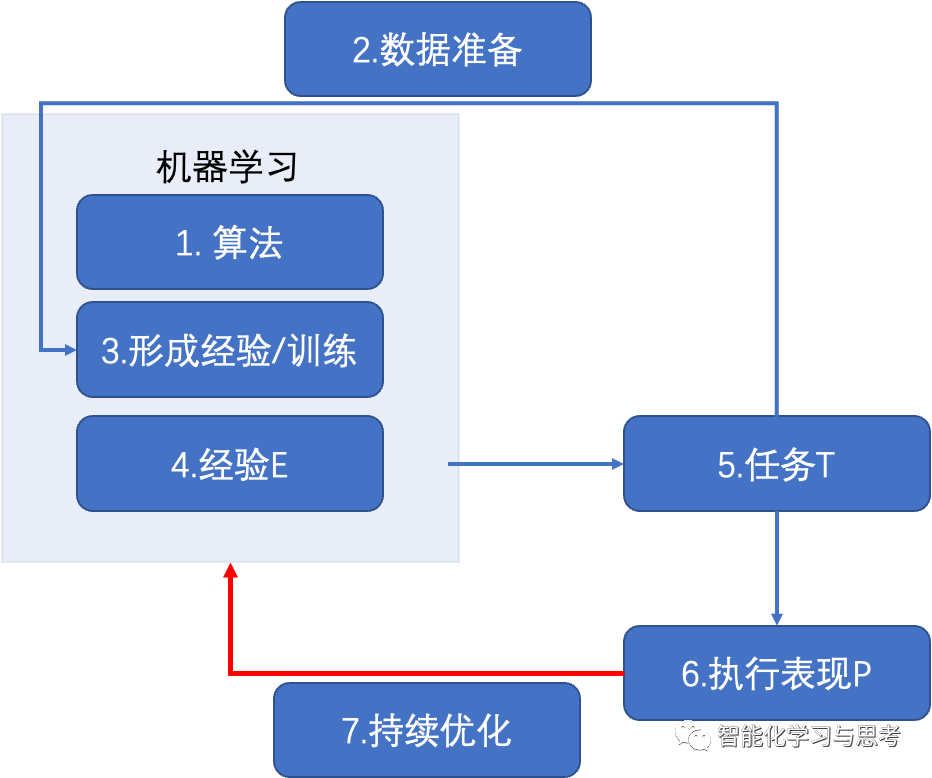
1. 选择算法。比如,刚才银行的例子,我们先要对客户进行分类找到黑名单,这是分类算法,也要通过客户行为预测他的额度水平,这是回归算法。前篇对于Transformer的讨论,就是一个最新的高级一些的算法。
2. 准备高质量的数据,并进行特征工程。通常这些要花费很多时间,特别是工业界,往往没有高质量的数据。这里数据质量有四个层面:一是绝对的数据量,这个好理解。二是样本数据,比如,在银行风控领域,如果只是交易数据,那不是样本,必须有真正的欺诈数据;比如,在设备管理领域,不但要有设备的运行数据,还要有设备的故障数据,这样机器才可以真正学习。三是数据的处理效率,对于AI真正有价值的往往是实时数据,这是发挥AI决策最大价值的关键。四是特征工程,只有数据是不够的,要进行处理,拿出机器可以理解而且有价值的特征才是根本。最简单的例子就是男、女要分别改成0或1。特征工程是AI计算最重要的领域,整个深度学习的神经网络可以理解为就是在做数据的特征工程。
3. 对数据用算法进行训练。这个训练的过程才是让机器有能力执行任务的关键步骤,而且很多计算算法的逻辑也针对的这部分。我们讲算力是决定性因素,也往往指训练阶段的算力瓶颈。
4. 训练结束一般还要做很多测试,确保这个经验是能够应对多种情况,从而真正形成经验E。
5. 经验E要用到生产系统,实时地执行任务T。比如,上面例子中,我们核心任务是对每个用户的信用额度动态调整。
6. 评估执行表现。AI的表现相对于人工会提升多少,和计划是否有偏差等。
7. 持续优化。这里的优化是全方位的,既要更新算法,提高数据质量,又要有更拟合的训练结果及更实时地执行任务等。经常听客户说,AI可能在我们这里落地效果不好。其实AI在哪里落地,刚开始时效果都不会好,真正让AI起作用,是需要持续优化。第四范式的很多AI驱动的客户,也把这一条当做自己重要的核心竞争力,即持续迭代的能力。
机器学习的理论基础
我们先从这个经验E如何训练出来谈起。 假设,这个经验E可以抽象成一个线性关系(当然现实世界不一定是简单的线性关系,这里只是简单化处理),即设Y=f(x)=wx+b,x是银行数据(比如:还款逾期率),Y是信用额度。我们要学习的经验E,就是学习这个f( ),这个概念很重要,建议停下来稍加理解。 要想得到f( ),需要先拿一些样本(也就是我们事先知道一些x数据,以及对应的y)进行训练。 例如:
| 信用额度 | 还款逾期率 |
| 100000 | 0% |
| 20000 | 5% |
| 120000 | 15% |
| 100000 | 12.4% |
| 80000 | 35% |
我们希望利用这些x到y的样本,反推出f( )这个线性函数。
如图1:在还款逾期率这个x和信用卡额度y这个空间里,我们有个很多样本,需要预测的是这条直线y=wx+b长什么样。
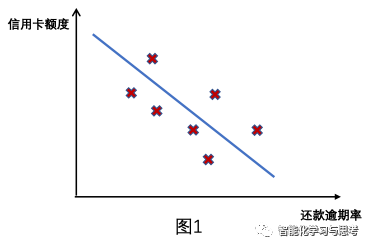
我们可以给机器设置一个规定的步长,穷举出很多y=wx+b。但应该选择哪个呢?
这里要引入:成本函数 J
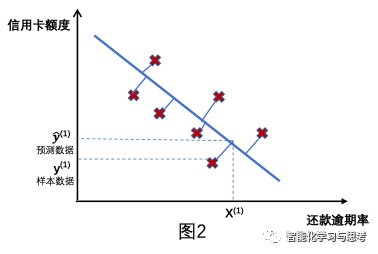

成本函数的简单定义:我们预测的直线到“每个样本的距离之和”的平均值。
假设我们选定了一条直线或者说一个f(),那么在X(1) 给定情况下,y(1)是样本对应的数值, 是f()得出的数值。M为样本个数。
是f()得出的数值。M为样本个数。
这个函数就是这条我们预测的直线到每个样本的距离之和的平均值。即我们应该找到一条直线,它距离每个样本的平均距离最短。也就是对应成本函数最低的那个。
这里可能大家有些懵,我们梳理一下:
这里有几个概念:真实世界发生的事件,被数据记录下来,被记录下来并拿来做
样本的,这三个层次是不是逐渐缩小了?再往后,我们训练产生一个y=wx+b,其目标是利用样本数据训练一个规律,从而可以预测真实世界。简言之,第一件事是训练出很多y=wx+b,第二件是比较哪个y=wx+b更好,第三件是选出那个最好的。
在实际操作中,计算机会算出各种可能的f( ),并算出相对应的成本函数,这个成本函数的取值就像图3显示的,是一个曲折的球面,机器利用规则在寻找那个山谷的最低点,也就是成本函数取值最小那个点,这个点所对应的f(),就是我们要找到的那个。这种方法就是梯度下降。
图3
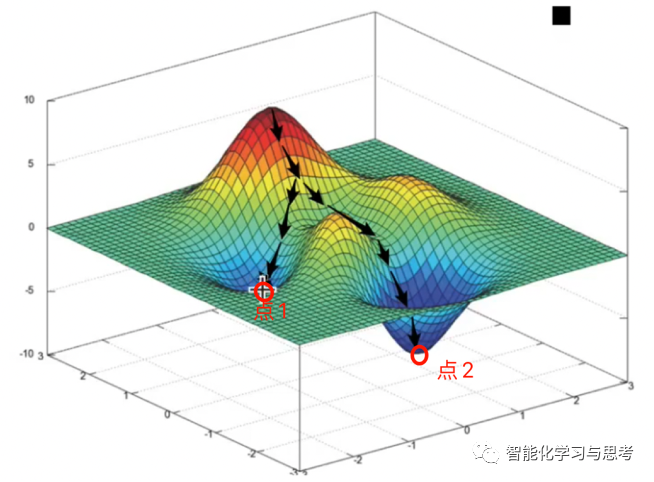
因此,计算机学习经验E的过程,就是给定一部分x,y数据(样本),预测总体上f( )长什么样。利用的方法就是通过梯度下降的方法,找到成本函数最低的那个f( )。
所谓梯度下降,其原理就是提前设置一个学习率。学习率是告诉计算机该以什么变动频率产生多个f( )用来比较。如果这个f( )是个线性方程,其中一个学习率就是这个斜率的变化。比如,机器预测这个方程式y=3x,如果学习率是0.1,那么下一个预测的就是y=3.1x。机器学习,就是这样每得出一个方程,就计算一个相应的成本函数,然后通过梯度逐步下降原则,找到成本函数最小的方程。
通过梯度下降计算后,选出最优f( ),计算机就能够完成任务T。在例子中就是,如果有新的还款逾期率数据,机器可以根据f( )预测相对应的信用卡额度,从而给出更合理的银行客户信用额度,因此提升了银行服务客户效率,带来了信用卡对应收入的提高。
机器学习的数学基础——向量
刚才那个例子,X是还款逾期率,也就是说只有一个变量。但现实生活中,影响信用额度的不只是一个变量。还会有性别、年龄、地区、年薪、存款额、信用卡交易额、违约次数等诸多特征,如下表(图4)。

图4 表格中是两个样本,每个样本都是一组数据,是银行客户的基本画像以及交易行为。银行客户的信用卡额度应该是这些信息综合决定。 这里每一行数据,称为一个向量;可以表示为: 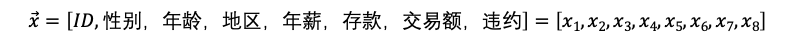 每个向量里都包含了各种特征数据。 向量是高维空间的某个点,在这个例子中这个高维空间就是由这8个特征类别组成的高维空间。 相比较y=f(x)在二维,y=f( )我们需要在这个高维空间去计算。 这个从y=f(x)到y=f( )的转换非常重要,是一定要理解的概念,整个AI的数学基础都建立在最小的计算单元——向量上。 为什么要升到这个高维度来看数据?这里有个背景,就是我们希望数学公式尽量是线性方程,而不是多元方程;只有当数据被放到一个非常大的维度中,数据才可以更容易呈现线性关系。
每个向量里都包含了各种特征数据。 向量是高维空间的某个点,在这个例子中这个高维空间就是由这8个特征类别组成的高维空间。 相比较y=f(x)在二维,y=f( )我们需要在这个高维空间去计算。 这个从y=f(x)到y=f( )的转换非常重要,是一定要理解的概念,整个AI的数学基础都建立在最小的计算单元——向量上。 为什么要升到这个高维度来看数据?这里有个背景,就是我们希望数学公式尽量是线性方程,而不是多元方程;只有当数据被放到一个非常大的维度中,数据才可以更容易呈现线性关系。
机器学习的进阶——神经网络
另外,在开始之前,有必要再介绍一下神经网络基础概念
我们定义样本数据:X(1) X(2) X(3) X(4)…X(i)
每个样本数据都是一个个向量形式,一共i个样本,
比如
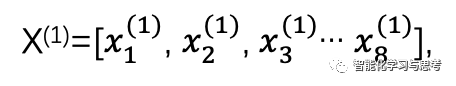
即每个样本有8个特征
如果我们把y=f( )换一个形式表达,就如下图
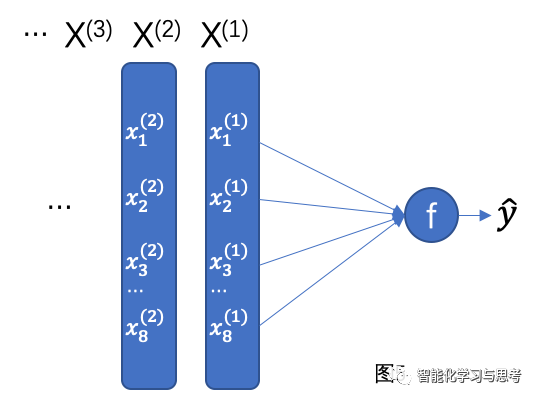
即每个X(1)的向量特征值参与计算,最后通过梯度下降的方法优化成本函数,得到f( )。
那么神经网络,就是在图5这个计算基础中间,加入了几个隐藏层,如图6就是加入三层隐藏层的神经网络。神经网络的作用主要是进一步提取新的特征,特别是那些隐藏的以及非线性的特征。
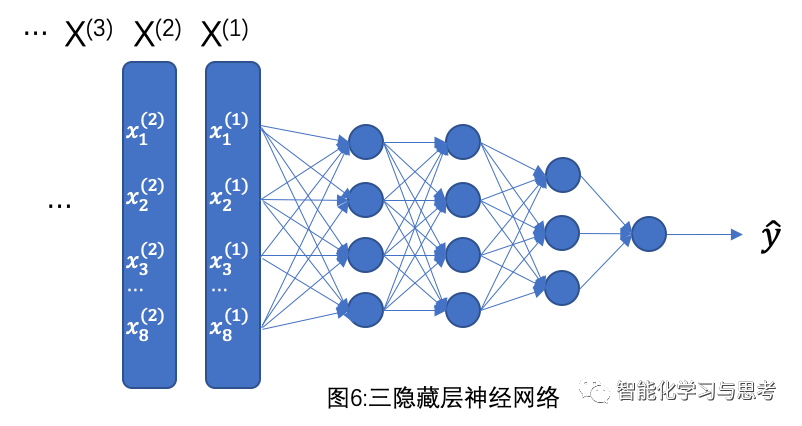
我们举个例子,还是信用额度计算问题(见图7),加入我们设计一层隐藏层,这个隐藏层对应的四个节点,分别是挣钱能力、还钱能力、对银行忠诚度、信用习惯,这四个特征是先前数据样本里没有提供的字段。这些节点要分别跟我们熟悉的八个特征逐一进行计算,找出其相关性,从而得到一个更精准的信用额度。
其中挣钱能力、还钱能力、对银行的忠诚度、信用习惯是我们为了便于理解而人为设置的,现实中机器可以自动计算出相应的可能隐藏层。
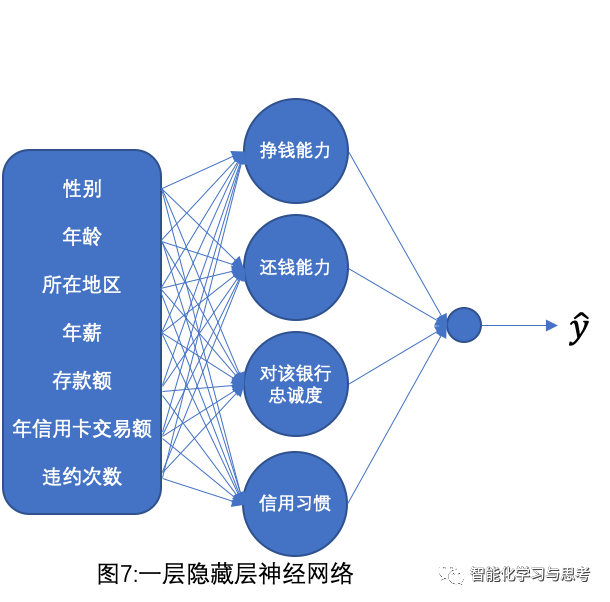
在很多神经网络里,这个隐藏层数可以达到几十层。某种意义上神经网络就是对数据原有特征的进一步补充,找出那些隐藏在数据里非线性的相关性,作为新的特征加以计算,提升模型能力,可谓之深度学习。深度学习是机器学习里面的一个分支,但目前在各行各业得到了广泛的应用。
简要总结
讲到这里,我们把机器学习的最基本概念做一个简要总结:
① 机器学习基础流程中我们要搞清楚什么是训练什么是执行,另外“持续优化”是重中之重;第四范式在这个层面上不断掉坑不断爬出来,有多年积累。未来企业的治理结构里很可能会设置核心竞争力北极星指标,并通过智能化加以实现;但真正的壁垒就是这个“持续优化”。
② 机器学习的“训练”部分就是找到f( ),即成本函数按照梯度下降的方法找到最优的f( )。大家理解了找f(),才能进入各种算法讨论。
③ 强调向量的概念。这里数学上的背景是,我们不希望总是处理多元方程或者叫非线性问题,往往把数据放到一个高维空间,总是可以找到线性关系,当然这增加了非常大的计算压力。这个高维空间的新世界,是我们一定要有概念的,虽然这有些反直觉,而且也没有物理上映射。
④ 神经网络是在给定样本,给定向量特征情况下,对数据特征进一步的补充和强化。神经网络或者深度学习是未来的发展方向,不需要不明觉厉,但可能会越来越多地听到。当然只从特征强化的角度,解释神经网络还是远远不够的,但至少是个不错的开始。
这样介绍AI其实很大胆,跟经典教科书不太一样,再次强调我是门外汉出身,只是学了一 点之后的经验之谈,会有很多错误也一定不全面,也许半年后回过头我会有不同的感悟和心得,到时再给大家补充。
编辑:黄飞
-
本人小白,求解labview的FPG是干什么的2012-11-16 3927
-
LABVIEW里面做吉利时的源表的程序时用node是干什么的?node in和node out是干什么的?2017-12-11 2748
-
求大神告知这是干什么的?2018-11-13 1953
-
ar识别图是干什么的2019-08-27 18503
-
覆铜板是干什么的2020-01-07 3066
-
uc/os钩子函数是干什么的?2020-04-08 3991
-
RTCALRMbits.AMASK是干什么的2020-04-30 1909
-
请问抽样定理是干什么的?2020-12-21 2365
-
伺服电机是用来干什么的?2021-09-28 5027
-
svpwm是干什么的2022-01-13 1120
-
串口它是干什么的2022-01-24 1070
-
晶圆厂是干什么的2018-03-16 108791
-
软件需求开发工程师是干什么的2019-03-13 4725
-
云服务器是干什么的2024-02-18 2436
-
美国云服务器是干什么的2024-02-19 1046
全部0条评论

快来发表一下你的评论吧 !

