

根据其谐波频谱内容重构DAC传递函数
描述
所有DAC都表现出一定程度的谐波失真,这是当DAC的输入由代表理想均匀采样正弦波的数字序列驱动时,DAC在其输出端再现完美正弦波的程度的指标。由于DAC的非理想瞬态和静态行为,输出频谱将包含谐波成分。DAC的瞬态输出特性包括压摆率限制、不对称上升和下降时间以及有限的建立时间。静态特性与传递函数如何偏离直线有关。本文重点介绍静态行为,并定义了一种从输出频谱中观察到的谐波成分推导出DAC传递函数的方法。该分析假设传递函数而不是瞬态输出特性是观察到的谐波失真的主要来源。这个假设在低频时是有效的。
DAC传递函数
图1显示了一个理想的DAC传递函数,即对角直线y=mx+b。数字输入位于 x 轴上,模拟输出位于 y 轴上。
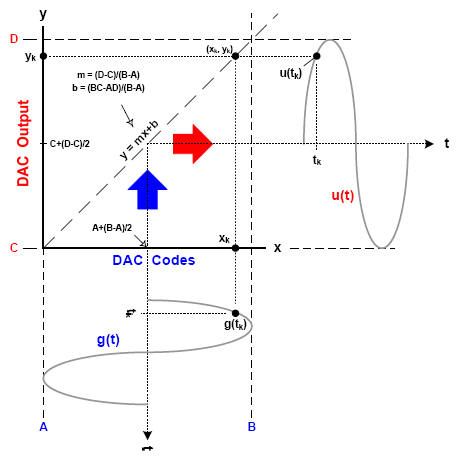
图1.理想的DAC传递函数。
x 轴上的感兴趣范围是从左侧的最小代码 (A) 到右侧的最大代码 (B)。y 轴上感兴趣的范围是从底部的最低输出值 (C) 到顶部 (D) 附近的最大输出值。定义理想传递函数的斜率 (m) 和 y 截距 (b) 的方程以边界值 A、B、C 和 D 表示。信号g(t)表示一个未失真的正弦波,由A和B范围内的数字输入组成,随时间向下发展。信号u(t)代表模拟输出,它跨越从C到D的值,时间向右发展。
输出信号是通过传递函数对输入信号的反射。请注意,输出信号是将 g(t) 上的每个点链接到 u(t) 上的关联点的结果。图 1 显示了特定时间时刻 t=t 的传输操作示例k,用于标识点 g(tk) 在输入信号上。反过来,传递函数链接 g(tk) 到相应的点,u(tk),在输出信号上。对于理想的线性传递函数,u(t) 将是 g(t) 的缩放版本。请注意,g(tk) 对应于点 xk在 X 轴上,通过传递函数反射到点 Yk在 y 轴上。耦合点集的先验知识 (g(tn),u(tn)) 可以识别关联的点 (xn,yn) 上的传递函数。因此,输入信号上的点g(t)和输出信号上的点u(t)之间的关系完全定义了传递函数。
对于N位DAC,边界值A和B具有特定值;即,A = 0 和 B = 2N–1.另一方面,边界值 C 和 D 可以方便地指定为 C = A 和 D = B。此分配意味着实际DAC输出信号的比例和偏移,因此其峰峰值跨度为0至2N–1.使用这些 A、B、C 和 D 值,理想的传递函数简化为 y = x,因为斜率和截距变为 m = 1 和 b = 0。
到目前为止,重点一直放在理想的DAC传递函数上,但我们现在有了处理失真的DAC传递函数f(x)的工具,如图2所示。需要注意的主要特征是传递函数不再是直线 y = x,而是形状函数 f(x),在这里任意显示为平滑弧。同样重要的是f(x)对输出函数u(t)的影响。理想输入 g(t) 反射传递函数 f(x),产生失真输出 u(t)。与任何现成的DAC相比,所示的传递函数被高度夸大,显示的戏剧性弧线仅用于说明目的。现代DAC的传递函数几乎不会偏离理想的直线,但即使是最轻微的偏差也会导致输出频谱中出现谐波杂散。

图2.失真的DAC传递函数。
DAC传递函数的成功重建依赖于确定每个点的能力,(xk,f(xk)),来自g(t)和u(t)的知识。这是一个两步过程:首先使用代表完美采样正弦波的数字序列驱动DAC输入,使用频谱分析仪测量DAC输出,并记录基波信号的幅度和尽可能多的谐波;然后将测得的谐波幅度转换为具有特定形状的传递函数。如果操作得当,通过将g(t)传递到f(x)来模拟u(t)将产生与测量值相同的谐波失真值。
第一步:测量DAC谐波
第一步需要一个输入序列,该序列表示以均匀间隔的时间间隔采样的完美正弦波的一个周期。目标是重建DAC传递函数,因此输入信号必须至少包含从0到2的每个DAC代码的出现一次N–1.输入序列需要 2 个以上N使用等间距的样本来执行每个DAC代码,实际上至少需要2N+3示例,以保证命中每个代码。以下公式产生 2 的完美正弦序列K带有 K ≥ N+3 的 DAC 代码。函数 round{x} 将 x 舍入到最接近的整数。

| 其中 n=0,1,2,3, ...2K–1 |
该公式假设DAC以直接二进制格式解码数字输入字,作为0到2的无符号整数N–1.对于失调二进制或二进制补码DAC,gn必须进行调整以指示负值。
数字序列 (gn) 以采样速率 f 重复输送到 DACs,因此DAC输出频谱包含频率f的基波信号0=fs/2K.谐波出现在2f处0, 3F0, 4F0和 f 的其他整数倍0.由于DAC输出频谱的采样性质,这些谐波的幅度受sin(x)/x响应的影响。因为 f0是 f 的一小部分s但是,sin(x)/x 响应几乎是平坦的,可以忽略。例如,对于 8 位 DAC,K ≥ 11 和 f0≤ fs/2048,因此 sin(x)/x 将不超过 0.39% (0.034 dB) 输出到 100千谐波。
精确重建传递函数f(x)需要根据一组谐波数(h)记录尽可能多的谐波幅度。这些整数以h = 1(基频)开始,以h=H结束,其中H是测量幅度的最高谐波数。例如,对于测量值 10千谐波,H = 10,谐波数的集合是 h={1, 2, 3, .. 10}。
接下来,将每个测量谐波的幅度(M)与其谐波数相关联。例如,M1是 1 的量级圣谐波(基波),M2是 2 的量级德·谐波,依此类推通过 MH.谐波幅度通常以相对于基波幅度(dBc)的分贝为单位。通过以下方式将 dBc 转换为线性单位:

其中 D 是以 dBc 为单位的测量谐波幅度。例如,如果 3 的大小RD谐波为 –40 dBc,则线性幅度为 M3= 10–40/20,或 0.01。M1始终等于 1,因为根据定义,基波的大小为 0 dBc。
第二步:重建DAC传递函数
该过程的第二步涉及将测量的谐波与传递函数相关联。f(x) 上的点取决于 g(t) 和 u(t) 上相应点之间的关系,因此频域中的谐波幅度必须首先转换为时域表示。请注意,g(t) 由 DAC 代码组成,这些代码与与 g(t) 的正弦形式相关的时间点具有一对一的对应关系。因此,包含g(t)的DAC码与时域有关。此外,由于u(t)通过f(x)与g(t)相关,并且g(t)是一个时域函数,因此u(t)也必须表示为时域函数。这允许每个时间点,tk,在 g(t) 中链接到其在 u(t) 中的关联时间点,这对于从 g(t) 和 u(t) 确定 f(x) 是必要的。
将谐波幅度转换为时域表示具有挑战性,因为f(x)必须与每个可能的DAC码(0到2N–1) 以 g(t) 为单位。由于g(t)是一个完美的正弦曲线,确保唯一性的唯一方法是将范围限制在正弦波单调递增的地方,如图3突出显示的部分所示。如果没有这样的限制,f(x) 上的单个点可以映射到 g(t) 上的两个点并导致歧义。
为了证明这种模糊性,想象一下向下滑动区域T。点 (xk, f(xk)) 在 f(x) 上现在可以与 g(t) 上的两个点相关联,这是不可接受的。通过将 T 的范围限制为所示的范围,歧义就不存在。由于g(t)是正弦曲线,因此所需的T范围对应于初始相位偏移为3π/2弧度的<>/<>周期。

图3.f(x) 和 g(t) 之间的关系。
g(t) 以 T 为界的事实意味着在 u(t) 上也有类似的界限。因此,将记录的谐波幅度转换为时域必须确保将u(t)限制在与g(t)相同的T范围内,如图4所示。

图4.g(t) 和 u(t) 的时域范围。
请注意,实际时间跨度 T 无关紧要,因为 f(x) 仅用于在 g(t) 和 u(t) 的振幅之间进行转换。为了简化分析,请归一化基频 (f0) 到 1。频率 2德·因此谐波为2,频率为3RD谐波为 3,依此类推。因此,谐波频率与谐波数(h)相同:fh=h.这种方便的关系简化了用于从谐波测量创建u(t)的数学,Mh.
正弦波的一般时域表示为:
 |
其中β是峰值振幅;θ 为初始相位偏移 |
每个谐波的时域表示,uh(t),可以通过用h代替f和M来实现h为β。但是,回想一下,g(t) 偏移了 3π/2 弧度。此外,g(t) 和 u(t) 之间通过 f(x) 的链接意味着 g(t) 和 u(t) 在相位上对齐。用 3π/2 代替 θ 可提供所需的对齐方式。在下面的等式中,请注意 0 ≤ t < 1,π 替换 2π 以将基波限制为半周期,如区间 T 所示:

了解每个谐波的时域表示后,uh(t),可以重建复合输出u(t),作为基波和谐波信号的总和:

回想一下,目标是通过关联g(t)和u(t)来重建DAC传递函数f(x)。此外,g(t) 必须正好由 2N样本,以便与 f(x) 上的点保持一对一的对应关系。因此,将 g(t) 的样本计算为:

| (n=0,1,2,3 .. 2N–1) |
由于 g(t) 由 2 组成N样本,从由 2 个样本集组成的 U(T) 样本集中重建 f(x) 似乎是合理的N样品。然而,事实证明,至少有 2N+3需要样品才能为小值 M 提供合适的精度h.考虑到这一点,按如下方式计算 u(t) 的每个样本:
 |
(n=0,1,2,3 .. 2N+3–1) |
请注意,这会导致 u(t) 包含比 g(t) 更多的样本。这使得 u(t) 和 g(t) 到 f(x) 的映射变得复杂,因为 u(t) 的多个样本可以对应于 f(x) 和 g(t) 上的单个点。因此,必须对特定的样本组进行平均,以便提供对f(x)的合理映射。以下伪代码演示了假设 N 位 DAC 所需的映射,2Ng(t) 和 2 的点N+3你的点(t)。阵列 DacXfr 由 2 个N元素,最初为零。执行代码后,DacXfr 数组的元素包含规范化的 DAC 传递函数。
n = 0
FOR i = 0 TO 2N–1
AvgCnt = 0
WHILE i = g[n]
AvgCnt = AvgCnt + 1
DacXfr[i] = DacXfr[i] + u[n]
n = n + 1
IF n >= 2N+3
EXIT WHILE
END IF
END WHILE
IF AvgCnt = 0
EXIT (fail because array, g[ ], is missing a DAC code)
END IF
DacXfr[i] = (DacXfr[i]/AvgCnt)/2N
END FOR
验证
为了验证本文中描述的方法,使用频谱分析仪测量由代表完美正弦波的输入序列驱动的14位DAC的输出。记录前2次谐波的幅度(数字15至1,单位为dBc),并使用这些值重建DAC传递函数f(x)。接下来,仿真通过重构的DAC传递函数f(x)传递理想的正弦输入序列g(t)来生成输出序列u(t)。FFT 将 u(t) 转换为其频域等效项 U(ω)。从U(ω)中提取谐波幅度,并与频谱分析仪测量值进行比较,如表7的表格结果所示。请注意,最大的误差,与 <>千谐波,仅为0.065分贝。
表1
| 谐波数 | 测量幅度 (dBc) | 模拟幅度(分贝) | 偏差(分贝) |
| 1 | 0.00 | 0.00 | 0.000 |
| 2 | -75.1 | -75.100 | 0.000 |
| 3 | -74.5 | -74.502 | -0.002 |
| 4 | -90.5 | -90.501 | -0.001 |
| 5 | -86.5 | -86.498 | 0.002 |
| 6 | -92.0 | -91.999 | 0.001 |
| 7 | -95.5 | -95.565 | -0.065 |
| 8 | -93.8 | -93.801 | -0.001 |
| 9 | -97.2 | -97.187 | 0.013 |
| 10 | -89.6 | -89.599 | 0.001 |
| 11 | -94.2 | -94.204 | -0.004 |
| 12 | -98.8 | -98.802 | -0.002 |
| 13 | -95.6 | -95.649 | -0.049 |
| 14 | -99.3 | -99.298 | 0.002 |
| 15 | -91.1 | -91.080 | 0.020 |
由于比例,重建传递函数的图显示为直线 (y = x)。事实上,传递函数实际上偏离y = x足以产生表1所示的谐波成分。它有助于仅绘制传递函数与理想直线的偏差,如图 5 所示。纵轴以 LSB 为单位。

图5.DAC传递函数的残余误差。
审核编辑:郭婷
-
传递函数中零点的解决方案2010-12-24 4461
-
由DAC谐波频谱成分重构其传递函数2011-05-25 3544
-
LCL滤波器传递函数和逆变器谐波的理解2019-05-24 0
-
自动控制原理_传递函数2016-01-18 903
-
传递函数的时域辨识2017-10-26 1439
-
传递函数的频域辨识2017-10-26 1606
-
DAC传递函数资料下载2021-04-27 623
-
传递函数极点和零点的影响是什么2021-06-12 9656
-
传递函数的频率特性2023-02-24 2895
-
各转换器的传递函数-升降压转换器的传递函数导出示例 其12023-02-24 1481
-
各转换器的传递函数-开关的导通电阻对传递函数的影响2023-02-24 996
-
如何列写无源网络传递函数2023-03-10 5202
-
开环传递函数是怎样影响系统的?2023-07-11 4033
-
传递函数和控制Block(上)2023-11-17 1310
-
传递函数的定义是什么 传递函数的拉氏反变换是什么响应2024-02-01 4682
全部0条评论

快来发表一下你的评论吧 !

