基于SMT的并发程序验证中约束求解问题

本文摘要

众所周知，(串行) 程序验证的复杂度极高。并发程序在大大提高软件执行效率的同时，也会显著增加程序执行的不确定性，使得并发程序验证的复杂度更高。有趣的是，并发程序中内存访问的执行顺序可以利用偏序关系进行建模。沿着这个思路，我们在基于 SMT 的并发程序验证方面做了一些探索，提出了一个专用于并发程序验证的 SMT 理论，设计了相应的判定算法。基于上述理论开发的并发程序验证工具 Deagle 获得 SV-COMP 2022 并发安全赛道冠军。

以下为正文。

# 背景 #

本质上讲，要验证一个程序的正确性，需要验证程序中所有执行都正确。对并发程序来说，由于线程之间的交织，不同线程中程序指令的执行顺序有很多种情况，导致并发程序的执行空间远大于同等规模下串行程序的执行空间。因此，并发程序验证的复杂度远高于串行程序。

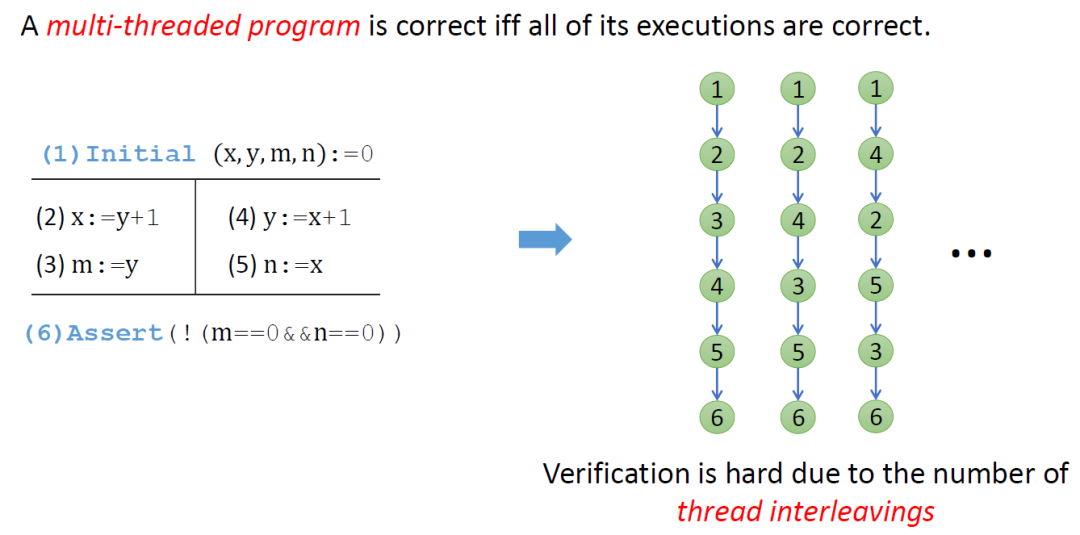
目前存在许多致力于缓解执行空间爆炸的并发程序验证技术，包括偏序规约 (Partial Order Reduction)、限定上下文切换次数 (Context Bounded)、惰性顺序化 (Lazy Sequentialization) 等。这些技术虽然在某种程度上可以有效降低需要考虑的程序执行的绝对数量。但从本质上来讲，仍然需要 (显式地) 遍历程序中的所有执行，验证规模仍然非常有限。

那么有没有可能像串行程序一样，将并发程序验证问题编码成 SMT 公式，再借助于 SMT Solver 进行求解？采用这种方案的好处是：编码成 SMT 公式后，程序的执行空间可以通过 SMT 公式的解空间来表达，由此可以借助 SMT 求解器，通过搜索 SMT 公式的解空间来隐式地遍历程序的执行空间。

# 一个简单的示例 #

并发程序编码的核心问题是确定不同线程之间程序指令的执行顺序。下面通过一个例子来展示如何将一个并发程序编码成 SMT 公式，后面再介绍怎么对编码得到的 SMT 公式进行更有效的求解。

下图左边展示了一个非常简单的并发程序，包含一个主线程和两个子线程。我们首先将其转换为 SSA (Static Single Assignment) 形式。注意这里的 SSA 与串行程序 SSA 的不同：串行程序 SSA 对每一次写操作引入变量的一个新拷贝，而并发程序 SSA 对于每一次读操作也需要引入变量的一个新拷贝。

Concurrent Static Single Assignment-1

得到并发程序的 SSA 的形式之后，就可以对其进行编码了。注意本例程是一个非常简单的不含分支的程序 (分支程序的编码后面再讨论)。不含分支的程序都可以转化为只含赋值语句和断言语句的程序。

如下图所示，每条赋值语句和断言语句都可以直接编码成逻辑公式，其中编码断言语句时需要对断言条件取反，称为错误条件 (Error condition)。

Concurrent Static Single Assignment-2

# 内存模型 #

为了刻画并发程序变量之间的读写关系，必须考虑 内存模型。

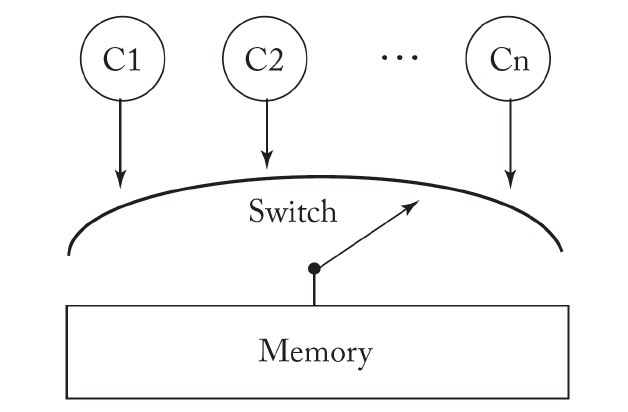
Memory Model

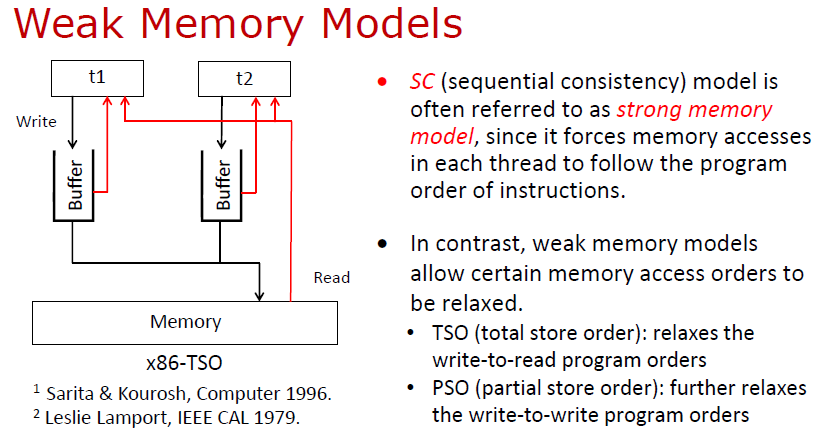
最简单的一种内存模型叫顺序一致性模型 (Sequential Consistency, SC)。在内存模型中，每个线程按照自己的指令序列发送访存指令到内存系统；如果最后访存指令被内存系统执行的顺序跟线程发送的顺序是一致的，就称为顺序一致性模型。很多情况下，顺序一致性模型也称强内存模型 (Strong Memory Model)。

与强内存模型对应，还有另一种内存模型，称弱内存模型 (Weak Memory Model, WMM)。内存模型与底层的硬件实现密切相关。硬件领域的许多优化机制在提高硬件处理速度的同时，也导致顺序一致性的假设不再成立。

为此，需要引入更弱假设的内存模型，即弱内存模型。常见的弱内存模型包括 TSO (Total store ordering)、PSO (Partial store ordering) 等。

为方便理解，下面的讨论主要聚焦于 顺序一致性模型。对于弱内存模型，我们将在最后进行单独讨论。

# 符号化编码 #

在对并发程序进行编码时，除了要考虑赋值，还必须考虑所有访存操作的执行顺序，为此引入 事件 的概念。每个事件代表一次访存操作。后面我们将基于事件来定义执行顺序。

设  为一个变量，以  表示对应这个变量的访存事件。在本例中，对变量 有四次访存 (读或者写) 事件。我们约定以上标 w 表示写事件，如 ；以上标 r 表示读事件，如 。

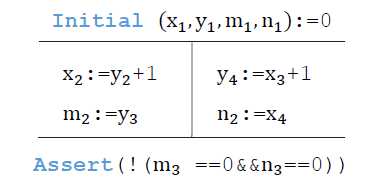
下面我们基于偏序关系 (Partial orders) 来定义访存操作事件之间的先后顺序。

# 符号事件图

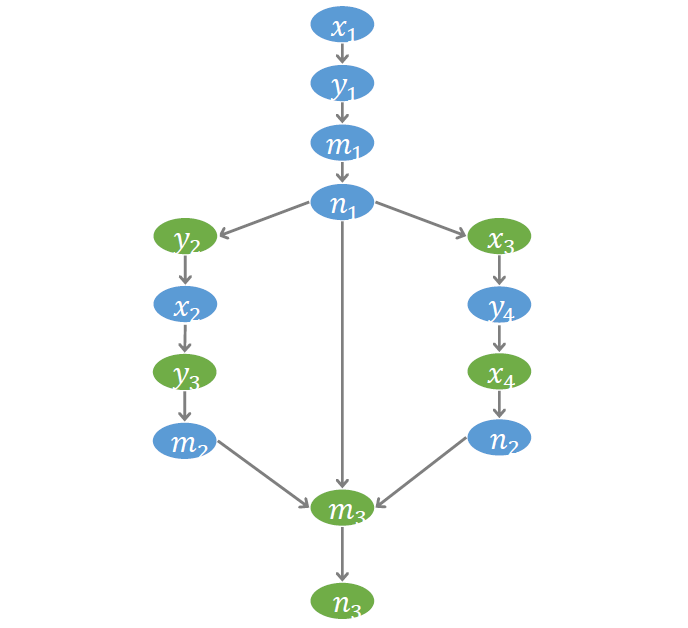
为了更好的刻画访存操作之间的偏序关系，我们建立了一个称为 符号事件图 (Symbolic event graph) 的结构。图中每个节点代表一个事件，每条边代表一个偏序。如下图， 到 有边，表示事件 发生在事件 之前。我们约定以蓝色节点代表写事件，绿色节点代表读事件。符号事件图对后面的验证算法非常重要。验证过程的许多推理都将在这个图上进行。

# PO 序

第一个需要刻画的偏序关系，叫做 Program Order (PO)，即访存操作被线程发出的顺序。对于顺序一致性模型，PO 序是程序执行必须遵循的一个顺序。但对于弱内存模型，在最后实际执行的顺序中，PO 序可能会被打破。

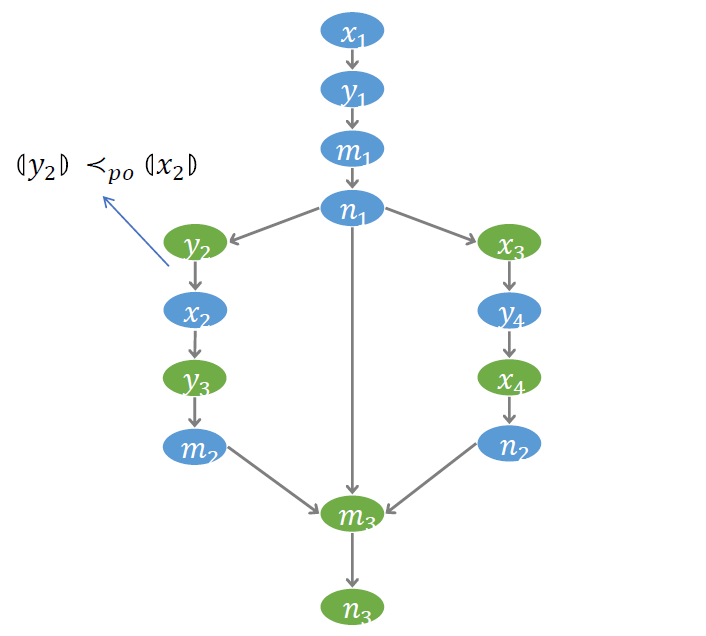
# RF 序

第二个需要刻画的偏序关系，叫做 Read-from (RF)，刻画了读操作读到的值与写操作写入的值之间的关系。

如示例程序中的 ，其读到的值可能来自于 ，也可能来自于 。为此我们引入两个布尔变量 和 。

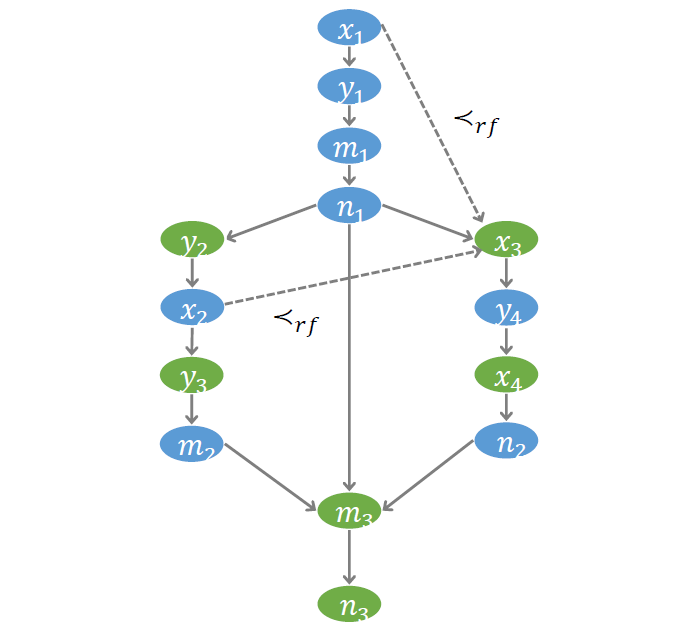
如下所示， 为真，表示 读到的值来自于 ；此时 对应的写操作必定发生在 对应的读操作之前，即 ，称为 RF-Ord 约束；

同时，在这种情况下， 变量的值一定等于 变量的值，即 ，称为 RF-Val 约束。

类似地，对应于 为真，我们也可以推导出类似的结论。

此外，由于 的值要么来自于 ，要么来自于 ，所以 和 必有一个为真，即 ，称为 RF–Some 约束。

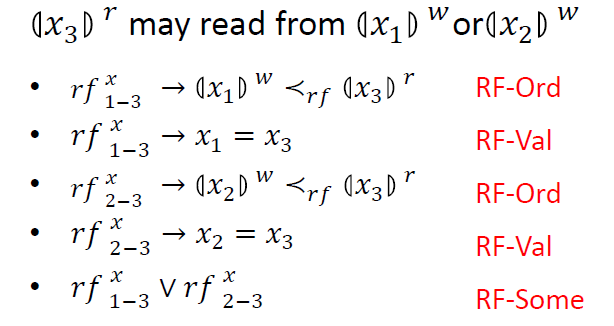
通过上述三种约束，就将变量之间的 Read-from 关系刻画出来了。

# WS 序

第三个需要刻画的偏序关系，叫做 Write-serialization (WS)。对于一个读操作，如果前面有对相同变量的多次写操作，则读到的值一定是最后一次写操作所写入的值。因此，对于同一个内存地址的多次写操作，必须考虑它们之间的执行顺序，称 WS 序。

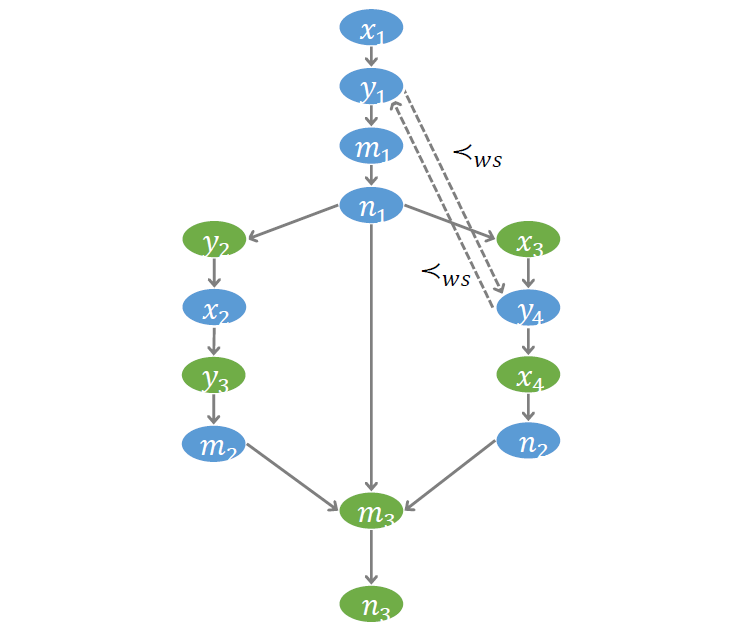
为了编码 WS 序，引入 WS 变量。每个 WS 变量都是一个布尔变量。例如，示例程序中的 、 都是对 的写操作。以 表示 在前， 在后的情况。

注意编码过程中需要引入大量 WS 变量。理论上讲，对相同地址的每一对写操作，都需要引入两个 WS 变量。

# FR 序

第四个需要刻画的偏序关系，叫 From-read (FR)。

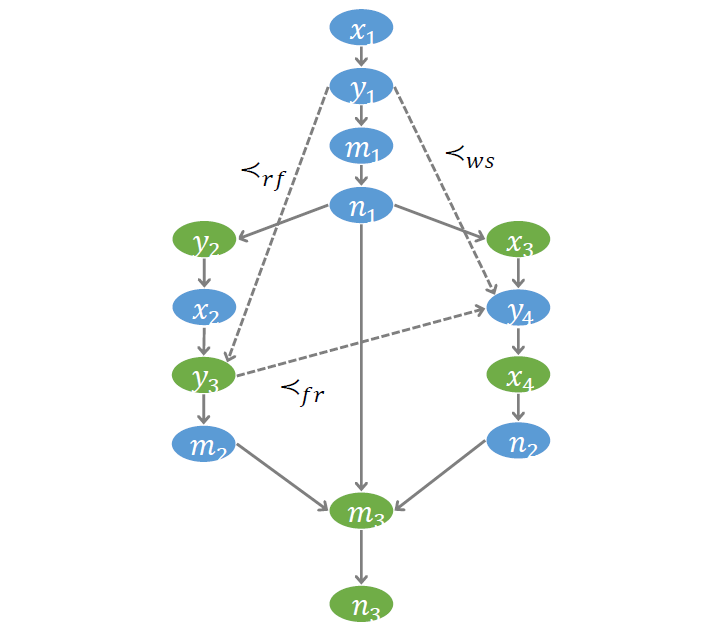
考虑示例程序， 是对变量 的读， 和 是对变量 的写；假设已知 读到的值来自 的写，并且 发生在 之前，则 一定也发生在 之前；否则 就成为距离 最近的写操作， 读到的值则应该来自于 而非 。即，

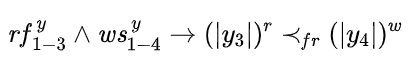
称该约束为 FR 约束。

在编码中需要引入大量 FR 约束。理论上，对每一对 WS 和 RF 变量，都需要引入一个 FR 约束。

# 验证条件

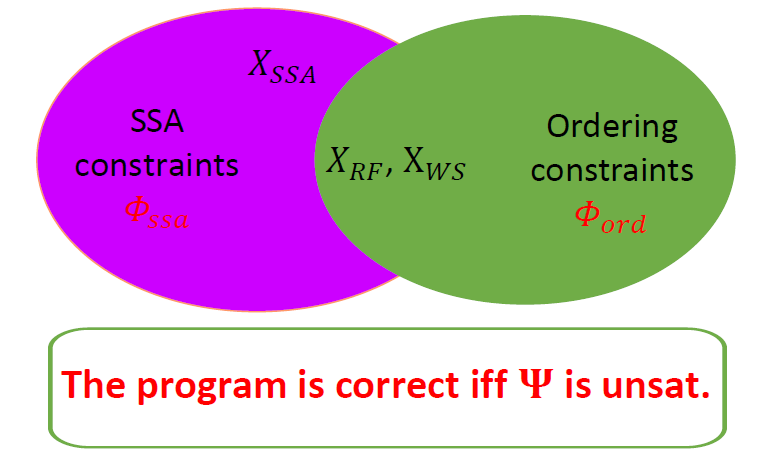
将前面所有约束 (包括针对赋值语句和断言语句引入的约束，以及针对执行顺序引入的约束) 进行合取，就得到了并发程序的验证条件 (Verification Condition)。该验证条件是一个 SMT 公式，后面的验证就可以交给 SMT Solver 进行求解了。我们可以证明：并发程序满足给定断言属性当且仅当其验证条件不可满足。

# SMT 理论 #

进一步分析上面的验证条件公式可以发现，整个公式分为 和 两部分，其中 只涉及布尔变量和偏序关系，而 中不涉及任何偏序关系。显然 可以直接采用现有的 SMT Solver 求解；而对于 ，目前缺乏直接对其求解的 SMT Solver。

在已有的基于 SMT 的并发程序验证方法中 (这些方法在符号化编码方面与我们的方法有一些差异，但基本上也可以分为 和 两部分)，大多借用已有的 SMT 理论来间接地解决 。它们为了比较程序中访存操作的先后顺序，会引入时钟的概念，即给每次访存操作打上一个时间戳，然后通过比较时钟戳的值来确定事件的先后顺序。在这些方法中，时钟戳一般被定义成整型变量，因此时间戳的比较可以通过已有的整型差分逻辑 (Integer difference logic) 来定义。

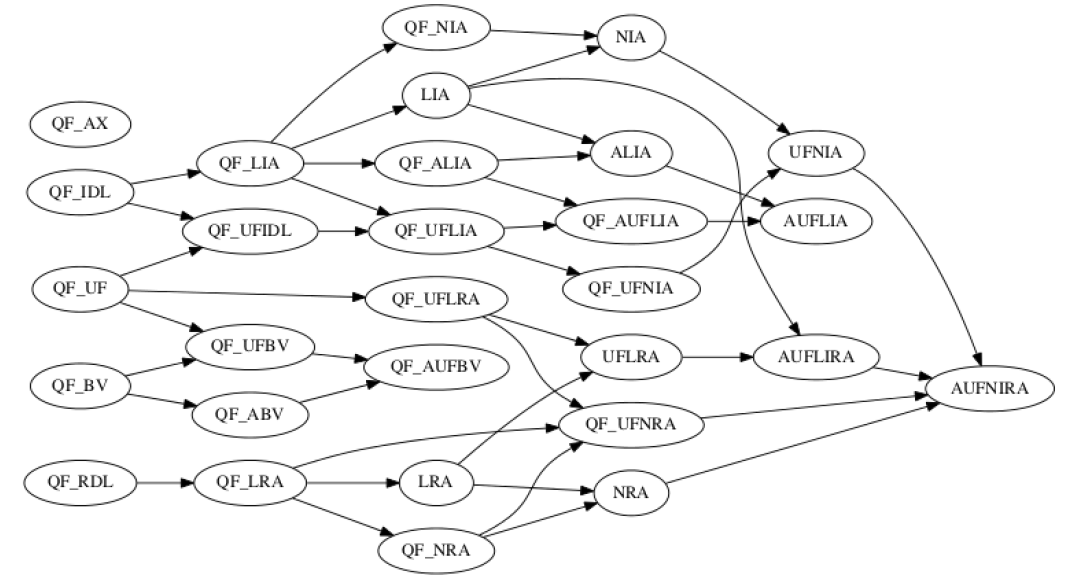
已有方案的缺点主要体现在以下两方面：

在这种方案下，为了比较事件的先后顺序，需要计算每个时间戳的确切值。事实上我们对于这些确切值并不关心。例如，考虑事件 和 ，设 和 是它们的时间戳，为了证明 发生在 之前，我们只需要证明 ，而无需计算出类似 的确切值。

更重要的是，在该方案下，为保证符号化公式编码了程序的所有执行，必须在编码阶段穷举上面介绍的所有约束。穷举编码需要引入大量变量，刻画大量 FR 和 WS 约束，这会给后端的 SMT Solver 带来严重负担，导致严重的效率问题。

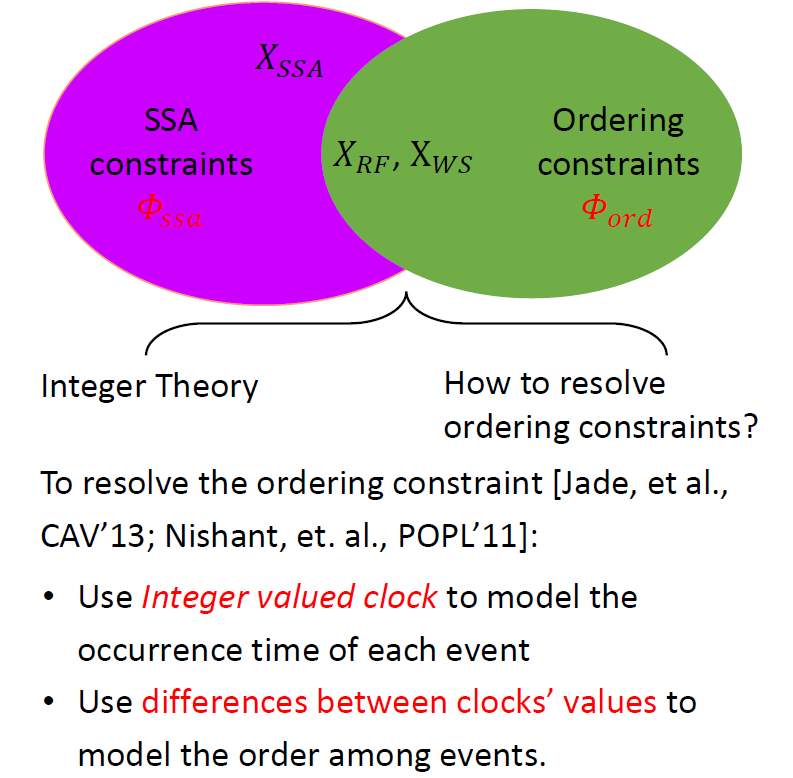
我们的主要想法是定制一个专属的 SMT 理论，称 序关系一致性理论 (注意这里的理论是一阶理论的概念)，用于描述和刻画 约束。我们这个新的 SMT 理论完全基于序关系来定义，不需要对事件发生的确切时间进行刻画。其次，我们还希望开发一个专用于 的判定过程，实现对 约束的更有效求解。

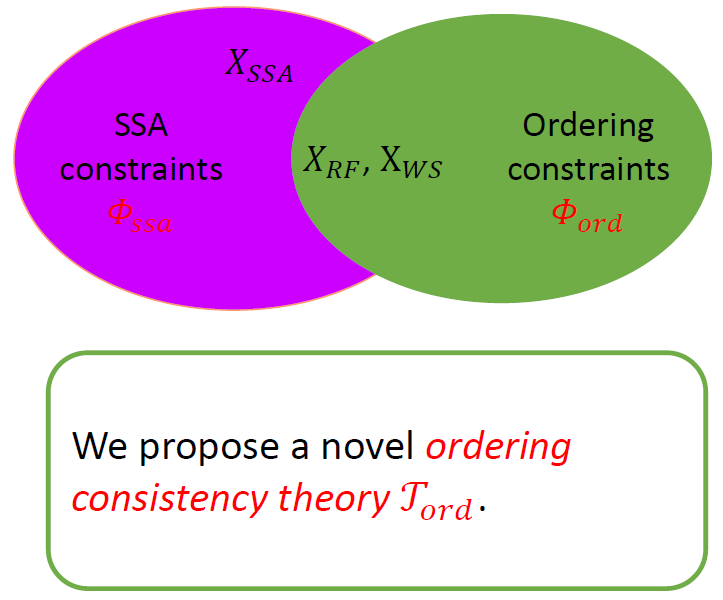
# 理论定义

在我们的 序关系一致性理论 [1] 中，分别以 表示 PO、RF、WS、FR 偏序关系， 表示访问事件。

主要包含下列三个公理：

第一个公理规定了 所代表的 偏序关系，以及这些偏序关系中对事件访存类型 (读还是写) 的要求。比如 RF 关系 要求 为写， 为读。

第二个公理规定了 FR 推理规则，即对于任意两个写操作 和一个读操作 ，如果已知 的值读自 (即 )，并且 先于 发生 (即 )，则 也必定先于 发生 (即 )。

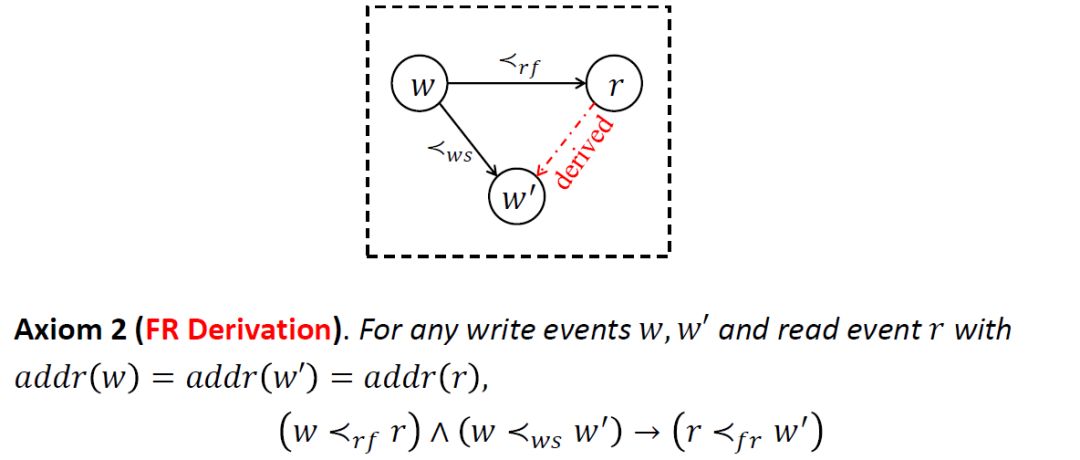
在 的判定过程中，我们会依据 FR 公理反复应用该推理规则，直至推导出所有可能的 FR 偏序关系。FR 公理的本质是将 FR 推导挪到 SMT 后端进行，这样在编码阶段就没有必要再去穷举所有可能的 FR 约束了。依据 FR 公理的推导是按需进行的，即只有在两个前提都满足的情况下才会推导结论中的 FR 关系。这种按需推理显然比穷举所有可能的 FR 约束更加有效。

第三个公理刻画的是 多种偏序关系之间的一致性。前面引入的 等偏序关系都是 happens-before 关系的特例。显然，所有 happens-before 关系的并集中不应该出现环，否则就会出现某个事件发生在自身之前的悖论。我们的判定过程正是依据这个公理来判定 公式的可满足性。

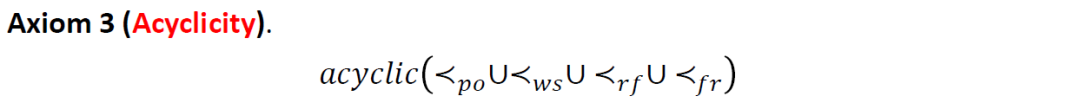
如下 Lemma 将程序正确性与 公式的一致性联系起来。给定程序的一条执行，如果它的访存操作的偏序关系满足一致性公理，就称该执行是一致的 (Consistent)，否则就称它是不一致的 (Inconsistent)。不一致的执行在真实的程序运行中不可能出现。

给定程序的一条执行，如果它满足待验证属性，就称它是正确的 (Correct)，否则就称它是不正确的 (Incorrect)。任何一条错误且一致的执行称为程序相对于待验证属性的反例。程序满足待验证属性，当且仅当程序中不存在任何一条反例。

#  判定过程 #

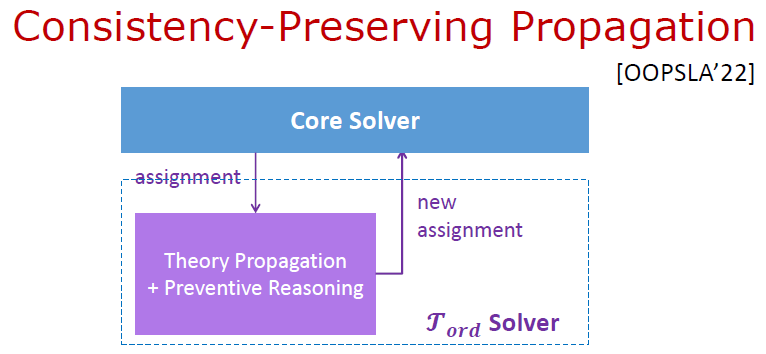
一个 SMT Solver 通常由一个 Core Solver 和若干个 Theory Solver 构成。每个 Theory Solver 实现一个 SMT 理论的判定过程，Core Solver 则负责 Theory Solver 之间的协调。下图即我们为 定义的求解器。

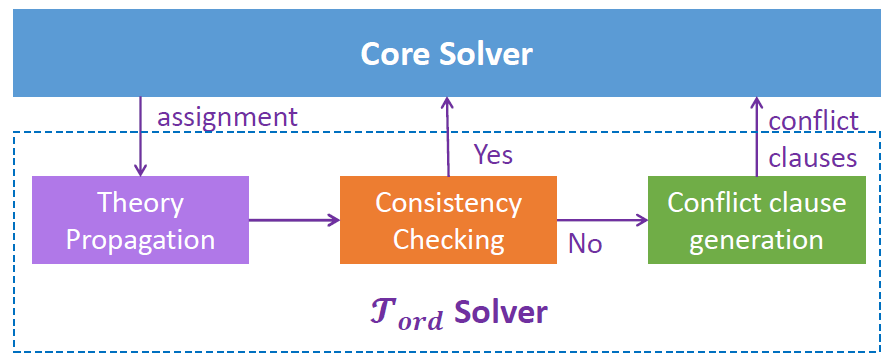
对应程序验证条件的 SMT 公式通常涉及很多 SMT 理论。给定一个 SMT 公式，SMT Solver 先进行初始化工作，将公式分解为 (可满足性等价的) 若干个完全属于某 SMT 理论的子公式。每个子公式再交给对应的 Theory Solver 进行求解。不同 Theory Solver 之间的信息交互由 Core Solver 负责。

下面只讨论针对 公式的判定过程。

第一步是 理论传播 (Theory Propagation)，即基于当前已知的偏序关系，尽量地去做 FR 推导。

第二步是 一致性检查 (Consistency Checking)。在理论传播的过程中会产生许多 FR 关系，所有这些关系都会被加入到符号事件图中，然后需要判断在当前符号事件图中是否存在环 (依据一致性公理)。

在一致性检查中，我们引入了一个 ICD (Incremental Cycle Detection) 算法，可以以一种增量式的方式进行检查，有兴趣的读者可以查看我们的论文 [1]。

第三步，如果在一致性检查中发现有不一致的情况 (即找到了环)，这时需要找出不一致的原因，并且以冲突子句的形式报告给 Core Solver。有关冲突子句生成的工作，有兴趣的读者可以查看我们的论文 [1]。

# 一些扩展 #

上面只讨论了不含分支的简单并发程序和 SC 内存模型，上述方法还可以很容易地被扩展到更复杂的程序和更一般的内存模型中。

# 针对分支和循环程序的扩展

分支的处理很简单，对应于每条赋值语句加入一个守护条件即可。循环的处理跟串行程序类似，要么引入一个循环不变式，要么将循环展开。不赘述。

# 针对弱内存模型的扩展

弱内存模型与强内存模型的主要区别在于，线程的访存操作最后被执行的顺序与线程发出来的顺序可能不一致，由此会导致更多的不确定性。前面已经提到，在顺序一致性模型下，并发程序的执行空间已经远大于同等规模下串行程序的执行空间；在弱内存模型下，程序的执行空间将再经历一次爆炸式增长。按照传统的基于执行空间显式遍历的方法，弱内存模型下的程序验证将变得异常复杂。

而我们的方法只需要很小的变动就能适应弱内存模型 (这里主要讨论 TSO 和 PSO) 的并发程序验证。

首先，弱内存模型的符号化编码只需要很小的改动。在所有涉及到的有关程序执行的偏序关系中，弱内存模型只会改变 PO 序。更确切的讲，弱内存模型只会松弛掉 PO 中的若干序关系 (具体松弛哪些关系跟所采用的具体的弱内存模型有关)，记松弛后的 PO 为 PPO (Preserved Program Order)。编码中，只需要用 PPO 去替代原来的 PO 就可以了，其他的编码都无需变动。具体细节请参看我们的论文 [2]。

其次，我们的方法还可以很容易的被扩展以考虑并发程序的原子性。我们可以给程序中的某个代码块打上原子标签，然后规定该代码块在执行过程中不能被其他线程打断。原子块中的指令是被 “打包在一起” 执行的，也就是说，在原子块外其他指令看来，原子块中的指令是同时发生的。

于是我们引入等价关系来刻画原子性。注意等价关系与偏序关系的不同，偏序关系代表两个事件前后发生，而等价关系代表两个事件同时发生。体现到符号事件图上，偏序关系用有向边表示，而等价关系则用无向边表示。

最后，弱内存模型的判定过程也不一样，主要区别在于一致性公理。在顺序一致性模型下，我们需要检查 4 种偏序关系的并集 是否无环。在弱内存模型下，尤其是带有原子性约束的弱内存模型下，一致性检查就没有这么简单了。具体的一致性公理这里不赘述，有兴趣的读者可以参考我们的论文 [2]。需要指出的是，虽然弱内存模型下的一致性公理比之前更复杂，但从判定过程来看，只需要对一致性判定算法进行改动，整个判定过程的框架跟前面还是一样的。

# 判定过程的进一步优化 #

第一个优化是 把更多的推理挪到 SMT 端。

在基本的 理论里面，只把 FR 推理放到了 SMT 端去执行，带来的好处就是前端不再需要编码 FR 约束，并且 FR 推理可以按需进行，导致 SMT 求解效率的大大提升。

进一步考虑将 WS 推导也放到后端。在前面所述 三大公理的基础上，进一步给出 WS 公理：给定两个写操作 ，和一个读操作 ，如果已知 的值读自 (即 )， 发生 (即其守护条件 成立) 且先于 发生 (即 )，则 必定先于 发生 (即 )；因为否则 就成为距离 最近的写，则 应该读自 而非 。

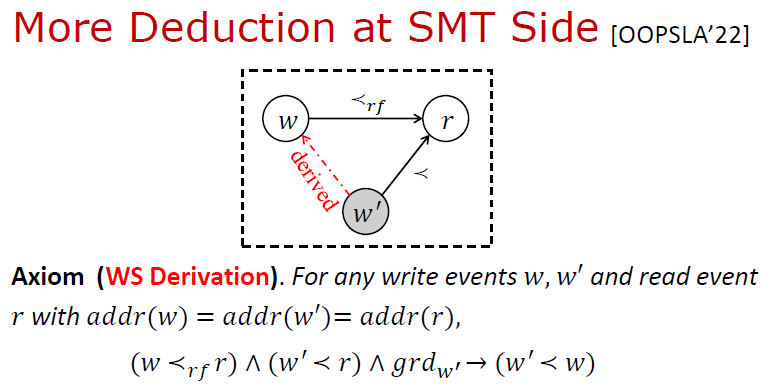
这样带来的好处是在前端不再需要引入 WS 变量和定义 WS 约束。WS 关系得以在后端以按需的方式进行推理，推理效率得到进一步提升。

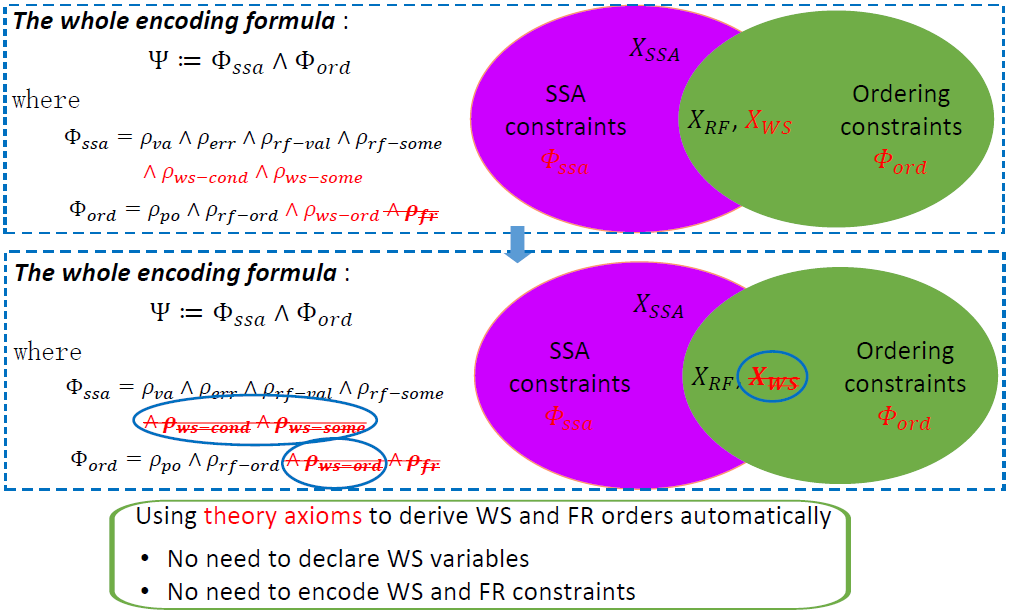
第二个优化是 在后端进行传递闭包计算。这样带来的好处是，之前的一致性检查需要在符号事件图中找环，现在只需在图中找自圈即可。

第三个优化是 预防推理 (Preventive Reasoning)。基本想法是为避免符号事件图中出现环，提前做一些预防性的推理。

如下图所示，如果图中已存在一条从 到 的路径，那么从 到 就一定不能再连边了，否则图上必然出现一个环 (违反一致性公理)。我们借鉴 SAT Solving 中单元子句 (Unit Clause) 的概念，称 到 的边为单元边 (Unit Edge)。在推理过程中，需要避免单元边被加入到符号事件图中。注意单元边可能迭代地由其他一些推理所导出，为了避免单元边，还要迭代地防止这些推理。

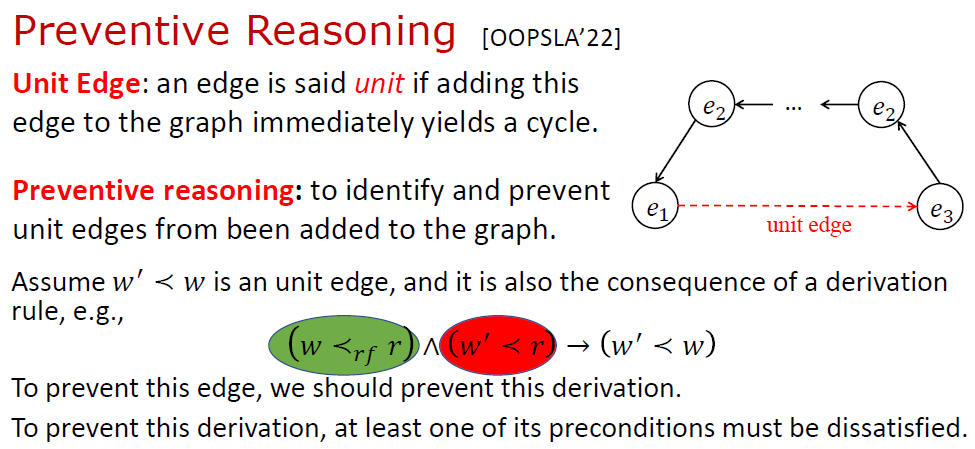
关于预防推理的详细内容，有兴趣的读者可以查看我们的论文 [3]。论文中我们证明了预防推理可以防止任何单元边被加入到事件图中，由此带来的好处是事件图中永远不会出现环。

加入预防推理后，Theory Solver 里面不再需要再做一致性检查和冲突子句生成的工作，只需迭代做 Theory Propagation 即可。

# 工具与实验：Deagle #

基于上述理论，我们开发了并发程序验证工具 Deagle [4]，参加国际软件验证大赛 SV-COMP 2022 并取得了并发安全赛道第一名 [5]，效率上远远优于其他方法。

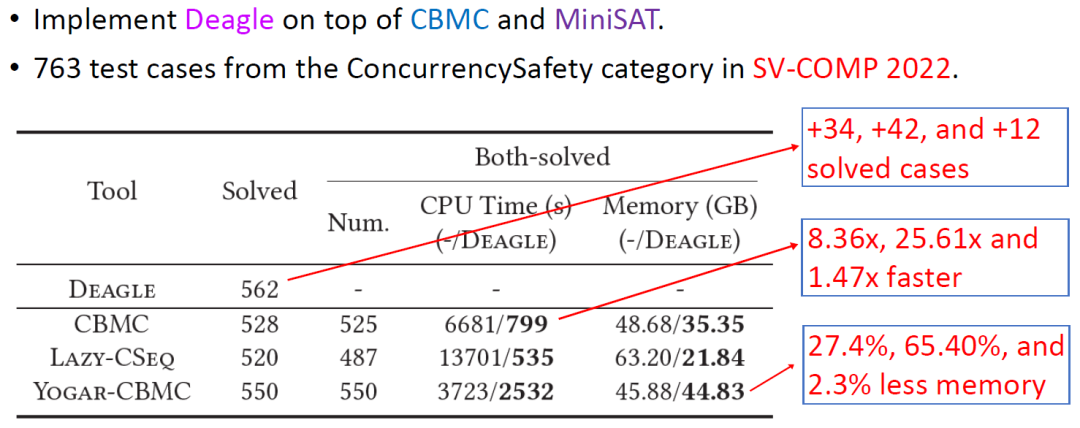
Evaluation

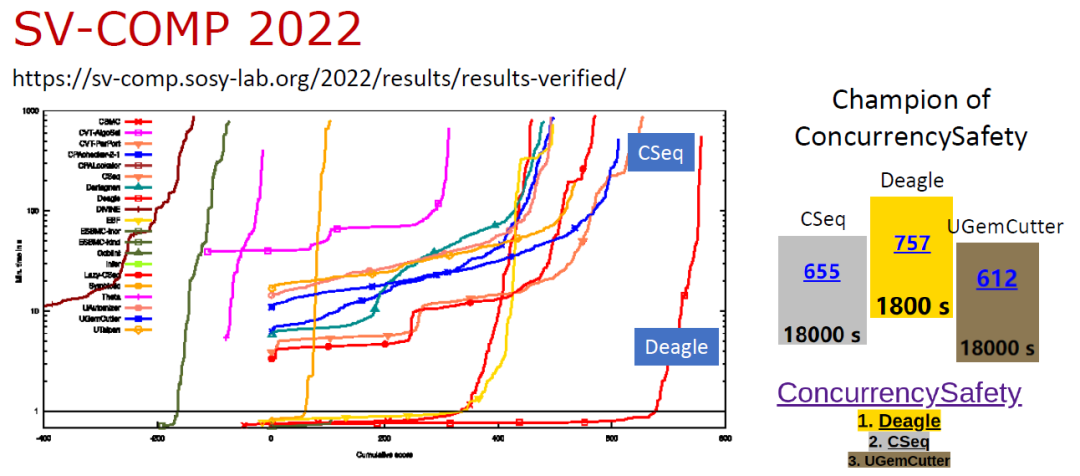
SV-COMP 2022

# 总结 #

我们对并发程序验证进行了一些探索，引入了一种基于偏序关系的符号化编码方法；提出了针对并发程序的序关系一致性理论，也针对这个理论开发了专属的 SMT 判定算法；开发的并发程序验证工具取得了不错的效果。

以上。

审核编辑：刘清