

非线性系统求解算法之增量迭代法进行讲解
电子说
描述
Part2 ·非线性系统求解算法
三、非线性系统求解算法
非线性系统求解难点在于,即在任何平衡构型下,切线刚度矩阵的计算取决于结构的变形几何形状和单元的内力(见part1刚度矩阵推导)。这些属性是从节点位移获得的,但节点位移是未知数。因此,无法解析求解平衡方程组,需要运用数值方法进行处理。
求解非线性方程组追踪平衡路径可分为单步法和增量迭代法,本文重点介绍增量迭代法。该方法将总载荷分解为一系列增量步,通过增量线性系统的直接或迭代求解获得相应载荷增量步的位移增量。因此,通过每一步中的一个或几个线性分析来近似施加载荷和节点位移之间的非线性关系。
求解非线性平衡系统的两类增量方法:第一种是纯增量或单步方法,其中使用单个刚度矩阵来表示每个分析步骤中的载荷位移关系。第二种是增量迭代法,它执行多次线性分析,在每一步迭代求解增量系统,以便在数值公差范围内收敛到平衡解。本文主要针对增量迭代法进行讲解。
1、增量迭代法求解公式
为了追踪平衡路径,必须以增量方式多次求解非线性方程组。非线性解通过每个增量的线性响应来近似。线性近似在线性化解和实际非线性解之间产生残差。该残差通过通过迭代进行收敛校正。在后文中,增量步i-1对应的构型是最新获得的平衡配置,而增量步 i 对应的构型是当前未知的需要求解的构型,符号Δ用来表示变量在每个增量步步的增量,符号δ表示每次迭代的增量。 切线刚度矩阵 K 在下式中定义,即内力对上一步对应的平衡构型下的节点位移的导数。
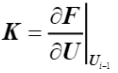 (26)
(26)
因此,内力表式为
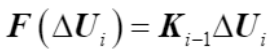 (27)
(27)
求解位移增量的增量系统表达式为,其中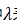 表示荷载比,
表示荷载比,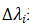 表示第i增量步荷载比增量,与总荷载乘积即为荷载增量
表示第i增量步荷载比增量,与总荷载乘积即为荷载增量
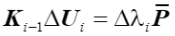 (28)
(28)
梁单元的切线矩阵的推导在part1中通过虚拟位移原理、运动学描述(更新拉格朗日法或共旋法)和有限元方法来离散每个单元位移场来得到。然而,由于内力是位移的非线性函数,方程的线性化增量系统的解不满足平衡。即外力和内力之间的不平衡,产生了残余力矢量。在每个增量中通常采用迭代过程,以通过消除残余力来确保平衡。
以上是增量步的解释,接下来对迭代步进行讲解。 考虑到结构在第 i-1 步处于平衡状态,希望在第 i 步达到平衡。为了消除源自线性化增量的残余力,通过在每个增量步骤中执行Newton-Raphson之类的校正迭代来完成的,直到满足收敛标准并建立新的平衡状态。
在每次迭代中,由下标 j = 1,2,3... 表示,得到对应迭代步的载荷比增量 δλij 和节点位移增量δUij。这些迭代增量表示相应步骤中载荷和位移值的校正。因此,在第j次迭代之后,通过累加迭代增量来更新第i步的总增量,如下式所示:
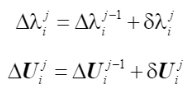 (29)
(29)
基于上述迭代步对荷载和位移增量的修正,整个分析的载荷比和节点位移的总值更新如下:
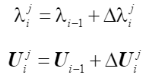 (30)
(30)
在第 j 次迭代后得到残余力矢量,由外部和内部节点力的总值之间的差值给出: 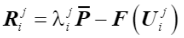 (31)
(31)
基于上述残余力矢量,可根据下式求得在第i步的第j次迭代中位移迭代增量
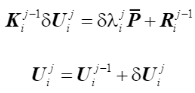 (32)
(32)
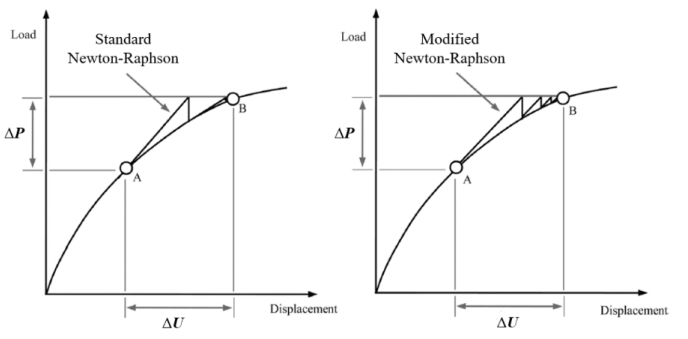
图12
上述迭代算法最常用的是Newton-Raphson迭代算法,如图12所示,标准 Newton-Raphson 迭代算法的切线刚度矩阵在所有迭代步都会进行更新,考虑大型系统时矩阵更新会耗费较多计算资源,因此可使用修正Newton-Raphson 算法,切线矩阵仅在每个增量步骤的开始进行计算,并在所有后续迭代中保持不变,即,对于 j > 1。修正Newton-Raphson 算法具有较低的计算成本 每次迭代都比标准版本,但收敛通常较慢,因为它通常需要在每个增量步骤中进行更多的迭代,但相较切向刚度矩阵更新耗费的资源来说还是值得的。对于上述方程x求解来说,因为存在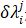 这个未知量,因此还需要一个附加方程来与之组成方程组进行求解,这个附加方程的一般形式为
这个未知量,因此还需要一个附加方程来与之组成方程组进行求解,这个附加方程的一般形式为
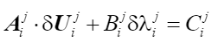 (33)
(33)
式中向量A和标量 B 和 C 是常数,可以根据不同的求解方法采用不同的值。上式x与组成的方程组写成矩阵形式为
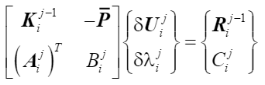 (34)
(34)
由于上述等式左端的矩阵不再是对称矩阵,所以在做大型计算时存储和计算上效率都会明显降低,为了克服这个问题,Batoz & Dhatt (1979) 提出了一种技术来克服这个问题,方法是将系统分解为两个使用原始切线刚度矩阵的系统,因此原始系统的带状和对称特性保持不变,具体如下所示
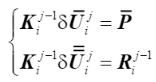 (35)
(35)
位移迭代增量的解是上述切线增量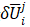 和残差增量
和残差增量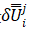 增量的线性组合:
增量的线性组合:
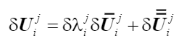 (36)
(36)
其中迭代步j对应的荷载比增量可通过下式求得
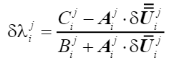 (37)
(37)
上述增量迭代法求解所用到的公式总结如下表所示
(1)增量迭代法求解步骤
上述增量迭代求解可分为两个阶段,分别为预测阶段和校正阶段。预测阶段相当于第一次迭代,其余迭代属于校正阶段。
① 预测阶段
在每个增量步,首先执行预测阶段的迭代。目的是使用上一步得到的切线刚度矩阵进行单次线性分析来计算预测解。具体来讲,这一阶段,对于第i个增量步,首先要进行初始切线刚度矩阵的计算,直接基于上一步结束时获得的结果(即节点位移 和内力对应的刚度矩阵)。
然后根据方程(35)通过线性分析计算位移的切线增量 。该阶段的残余位移增量为零,因为忽略了来自上一步的残余力。位移的预测增量, ,可根据方程(36)获得。但仅是位移的切线增量乘以载荷比的增量。载荷比增量是用约束方程(37)计算得到的,该约束方程定义了一个超曲面来限制增量迭代方法的校正解。下图13为单自由度系统的预测阶段示意图。
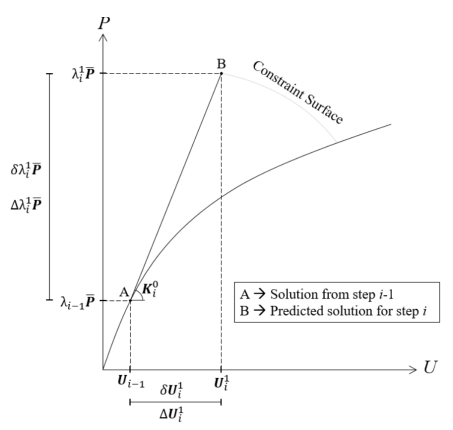
图13
因此预测阶段的求解的核心目的就是计算预测荷载比增量。在某分析过程的第一个增量步的预测阶段荷载比增量须人为指定,一般为最大荷载的10%~20%。在接下来的迭代过程中,荷载比增量则由约束方程(37)所定义的迭代算法进行计算,后文荷载比增量的计算方法本质就是对约束方程(37)的定义。
预测阶段荷载比增量对求解有很大的影响,直接与收敛性相关。该阶段,荷载比增量过大可能导致收敛问题,荷载比增量过小耗费计算资源,精度的提高也有限。因此使得程序能够自动根据非线性程度调整预测阶段的荷载比增量是一个优秀的非线性算法所应具备的功能。
即当结构响应基本程线性时,提高增量,当非线性较大时,减小增量。而且当求解至荷载极限点达到一个即将失稳的平衡态时,所追踪的位移增量对应的荷载增量必须是负值才符合常理,因此算法还应能够判断增量正负的选择。
a、预测阶段荷载比增量计算方法
荷载比增量的计算取决于约束方程(37)的定义,本节计算方法本质即约束方程的定义。两种计算预测阶段荷载比增量的方法,一种基于迭代次数的计算方法,另一种是根据系统刚度的计算方法。本文重点针对第一种方法进行介绍。基于迭代次数的计算方法计算预测阶段荷载比增量的方法又可以分为三类:
荷载增量法;
外力功增量法;
弧长增量法。
我们重点介绍第三种弧长增量法,因为弧长法的优势在于在于可以追踪平衡路径,准确捕捉snap-through和snap-back现象,如图14所示。为了数值算法上增量步大小一致性,校正阶段也采用同类型的弧长法。弧长法公式具体推导过程大家可参考相关文献,这里只列出用圆柱弧长法和球形弧长法计算预测阶段荷载比增量的最终公式
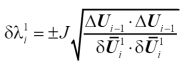 (38)
(38)
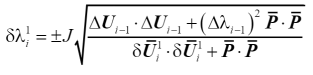 (39)
(39)
其中J为迭代调整因子,表达式如下
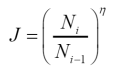 (40)
(40)
式中,Ni 和 Ni-1 分别是当前增量步所需的迭代次数,以及前一增量步中实现收敛的迭代次数。指数变量 η 通常在 0.5 到 1.0 的范围内,但通常采用较低的值。
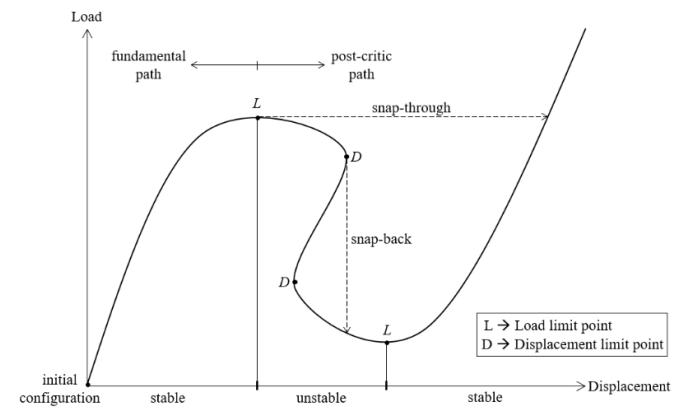
图14 b、预测阶段荷载比增量符号计算方法
上文提到预测阶段的求解的核心目的除了需要确定荷载比增量大小外,另一个重要的工作就是完成荷载比增量正负符号的确定。确定荷载比增量符号最常见方法的是基于刚度参数的行为进行确定,这些刚度参数常见的有 CSP(Current Stiffness Parameter)和 GSP(Generalized Stiffness Parameter)。因为参数CSP会在位移极限点附近出现一些数值不稳定性,所以本文主要介绍更为通用的GSP参数。GSP的具体表达式为
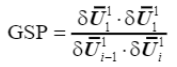 (41)
(41)
可以看出,GSP参数的分子是一个正数,分母由当前和前一步位移向量的标量积给出,该标量积的符号可以反应前一步和当前步的增量是否在同一个“方向”上,如果同向则为正,如果反向则为负,如图 15所示。当两个增量步之间存在荷载极限点时,两个位移向量的方向是不同的,因此GSP<0。因此,每次 GSP为负值时,必须反转预测阶段的荷载比增量的符号。增量符号可根据下式确定,其中初始增量步假定增量符号为正值。
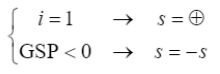 (42)
(42)
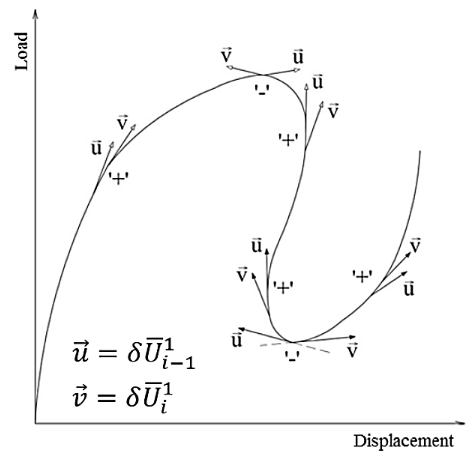
图15
(2)迭代矫正阶段
增量迭代方法的校正阶段旨在通过迭代循环消除由预测阶段产生的残余力来恢复结构平衡。该迭代循环从更新总荷载比和总节点位移 开始,将预测增量(和 )添加到上一步的结果( 和 )。随着几何构型的更新,相应的内力 被计算出来,残余力可以通过外部和内部节点力之间的差异来获得。
检查迭代是否收敛的方法,最常见的是基于残余力、残余位移或这些残余结果产生的功。本文采用的收敛标准是基于力的检查,如下式所示
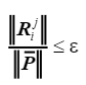 (43)
(43)
式中,分子分母分别为残余力矢量和参考载荷矢量的欧几里得范数,,该比率必须低于给定的容差ε,通常在 10-5 到 10-3 的数量级。如果满足收敛,则预测解被认为平衡状态,可致性下一增量步,否则开始第一次校正迭代。 每次校正迭代的第一个过程是计算切线刚度矩阵,要根据最新构型的节点位移和内力来对刚度矩阵进行更新。如果采用修正Newton-Raphson 迭代方案,则跳过此步骤,并使用在预测阶段的切线矩阵。如方程(35)所示,位移的切线增量和残余增量分别用参考载荷矢量和最后获得的残余力矢量计算。
然后,根据相应的约束方程(37)计算载荷比的迭代增量。最后,用方程(36)得到位移的迭代增量。。 载荷比和位移的迭代增量取决于约束方程(37)定义的超曲面。如果执行的迭代不仅涉及位移修正,还涉及载荷比的修正,则称为连续法,因为它可以跟踪超出极限点的平衡路径,例如上小节提到的弧长法。在这种情况下,控制修正解的约束面在一个或多个点处与平衡路径相交。
获得修正解后,接下来的程序与检查预测解的收敛性相同:更新载荷比和节点位移的总值,计算外力、内力和残余力,最后检查当前迭代解的收敛性。图16 给出了所描述过程的示意图。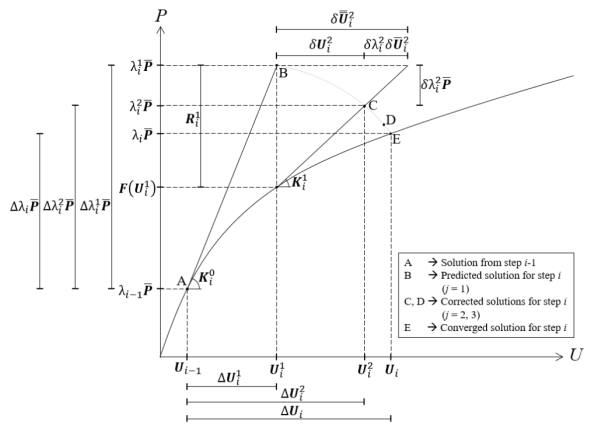
图16
与预测阶段的荷载比计算方法相对应,迭代阶段的荷载比增量计算方法同样有荷载控制法、外力功控制法和弧长控制法(还有其他多种方法,就不一一列举)。
传统的牛顿拉普森迭代法本质就是荷载增量控制法,在每个增量步中使用固定量的荷载比增量即预测阶段的荷载增量,并在每次迭代后保持不变。执行校正迭代仅通过位移校正来满足平衡要求,如下图17所示。
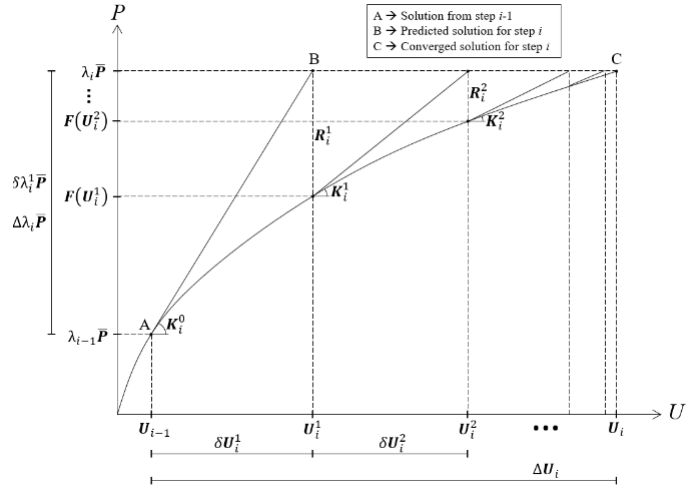
图17
当试图解决荷载极限点问题时,这种方法的存在明显的缺陷。一旦在预测阶段定义了固定荷载比增量,如果在增量中出现极限点,就无法修改荷载矢量。
尽管可减小的载荷比增量使其缓慢地接近极限点,但由此产生的刚度矩阵接近奇异的性质使得难以追踪结构的后极限状态响应。图 18 显示了使用荷载增量控制法跟踪具有snap-though行为的系统的平衡路径时的典型结果。
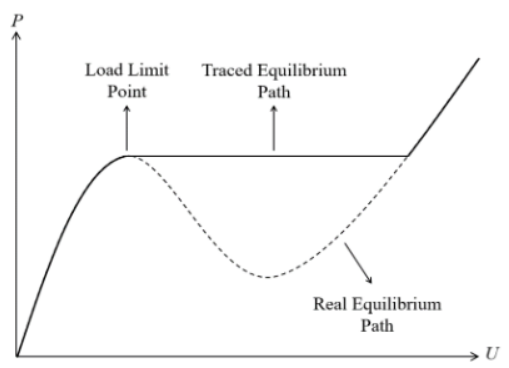
图18
本文重点介绍适应度较强的弧长控制法,弧长法的优势在于在于可以追踪平衡路径,准确捕捉snap-through和snap-back现象。由于弧长法也分多种,如线性弧长法和恒定弧长法。这里仅介绍恒定弧长法,即由位移和载荷增量的范数定义的弧长增量 ΔL 在整个迭代过程中保持不变。推导过程省略,这里直接给出恒定圆柱弧长法计算迭代步荷载比增量的公式
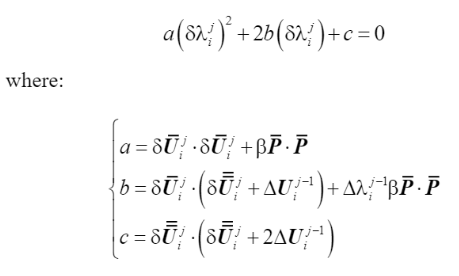 (44)
(44)
求解上式可得迭代步荷载比增量的显式表达式
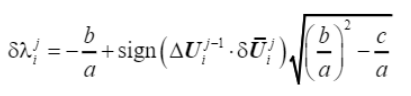 (45)
(45)
审核编辑:刘清
-
matlab牛顿迭代法全解2012-03-08 44365
-
问题:matlab实现牛顿迭代法求解非线性方程2014-07-05 14392
-
非线性系统描述函数法2016-05-31 1992
-
基于牛顿迭代法的FPGA定点小数计算2019-07-18 3286
-
参数寻优的迭代法的基本原理是什么?伺服控制系统常用参数寻优算法是什么?2021-10-13 1507
-
一类非线性系统迭代学习控制的初始态鲁棒性2009-05-30 730
-
非线性系统输出反馈控制2009-08-13 624
-
具输入饱和之非线性系统适应控制器之设计2009-10-31 686
-
非线性系统辨识2009-12-22 790
-
非线性系统辨识模糊模型参数收敛问题研究2011-08-19 895
-
高斯-牛顿迭代法简介2016-01-08 828
-
使用MATLAB编程实现里查森迭代法线性方程组求解的资料和程序免费下载2019-08-09 1139
-
牛顿-拉夫逊迭代法原理及其实现2023-04-17 4803
-
浅析非线性系统的相平面法2023-06-30 7025
-
python牛顿迭代法2023-11-21 1808
全部0条评论

快来发表一下你的评论吧 !

