

射频功率的测量和控制
模拟技术
描述
图 1.显示了典型的现代通信信号链。要传输的信号由数模转换器(DAC)在基带上产生。然后将该信号混频到中频(IF),在那里进行滤波,然后再混频到最终的射频(RF)。 在接收侧发生逆变换。接收到的信号被放大,混频至IF并滤波,然后混频到基带进行数字化。
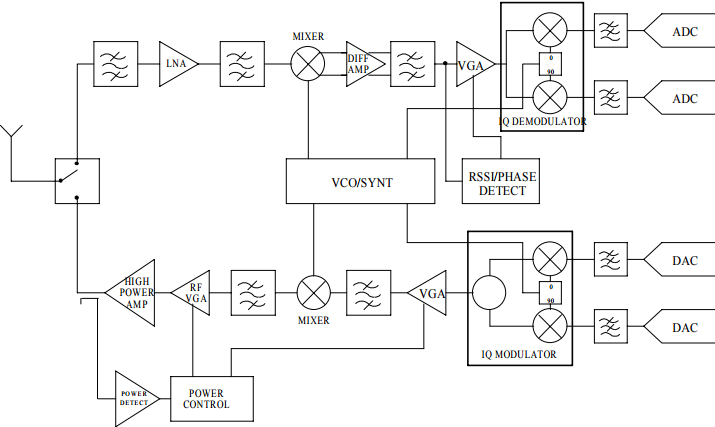
图1:现代RF信号链
虽然此类信号链有各种形状和尺寸,但通信应用中普遍需要测量和控制信号功率。在发射端,我们必须确保功率放大器(PA)符合监管辐射要求。我们还必须确保 PA 的传输不会超过某个功率水平,这会因过热而造成损坏。
在接收端,输入信号电平通常会在某个动态范围内变化。这可能是由于天气条件或接收信号源远离接收器(例如,在快速汽车中操作的移动听筒)。通常,我们希望向模数转换器(ADC)提供恒定的信号电平,因为这将最大限度地提高信噪比(SNR)。为此,接收信号链通常使用一个或多个可变增益放大器(VGA),这些放大器由完成自动增益控制(AGC)环路的功率测量器件控制。请注意,虽然发射功率控制可以在RF或IF进行,但接收侧信号处理通常在IF进行。
在这两种情况下,信号强度测量的精度都可能至关重要。例如,考虑一个基站,其传输的平均功率为 +50 dBm (100 W)。如果调节基站发射功率的检测器在温度范围内具有±3 dB的不可预测误差,则基站可能会在某个点被定向传输53 dBm(200 W)。这显然是不可接受的,因为它会增加装置的额外热尺寸成本过高。
在接收端,不精确的测量电路将导致提供给ADC的信号电平不佳。这将导致ADC过载(输入信号太大),或者浪费宝贵的动态范围(输入信号太小)。
本系列涉及与测量和控制RF功率电平相关的许多问题。将研究各种功率测量技术,如二极管、热、均方根直流和对数放大器。还将研究响应时间、动态范围、分辨率、变化的波峰因数、温度稳定性、尺寸和成本等问题。
权力
以瓦特为单位的功率可以用多种方式表示,即

其中V是均方根电压,I是均方根电流,R是功率耗散的电阻。由于大多数通信系统具有恒定的负载和源阻抗,通常为50 Ω,因此我们只需要知道均方根电压即可计算功率。因此,许多实际的功率测量电路依赖于测量均方根电压。
在dBm、dBmV、W、RMS和峰峰值电压之间进行转换
有线通信应用中的信号电平通常以dBm为单位。然而,对于那些具有电压响应的“功率”检测器,我们实际上应该指定相对于其输入电压的输出电压。对于生活在dB世界中的人来说,这可能会非常令人困惑。由于输入信号的峰均比发生变化,许多检测器的响应会发生变化,因此问题变得更加复杂。
dBm 单位定义为以 dB 为单位的功率电平,以 1 mW 为基准,即
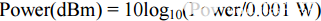
其中功率以瓦特为单位指定。
由于以瓦特为单位的功率等于均方根电压的平方除以阻抗,我们也可以将其写为
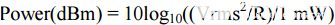
因此,0 dBm 等于 1 mW,+10 dBm 等于 10 mW,+30 dBm 等于 1 W,依此类推。由于阻抗是该等式的一个组成部分,因此在讨论dBm电平时,我们通常应指定线路阻抗(例如20 dBm:Re 50 Ω)。
dBV 单位定义为以 dB 为单位的电压电平,以 1 Vrms 为基准,即
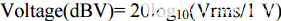
因此,0 dBV等于1 Vrms.图2显示了均方根伏特,峰峰值伏特,dBV,dBm和mW如何相互关联。但是,这仅适用于负载阻抗为 50 且波峰因数为 1.4142(即 Vrms = Vpeak- 峰值/2/1.4142 的正弦波)。请注意,在 50 系统中,dBV 和 dBm 之间存在 13 dB 的恒定偏移 (dBm = dBV + 13)。

图 2:功率和电压之间的转换
RMS的定义1
RMS(或均方根)是交流信号幅度的基本测量值。它的定义既可以是实用的,也可以是数学的。实际定义:分配给交流信号的均方根值是在相同负载下产生等量热量所需的直流量。例如,1 Vrms 的交流信号将在电阻器中产生与 1 Vdc 信号相同的热量。根据数学定义,电压的均方根值为,

这涉及对信号进行平方、取平均值和获得平方根。平均时间必须足够长,以允许在所需的最低工作频率下进行滤波。
波峰因数的定义
波形的波峰因数是其峰值与其均方根值的比值。幅度对称方波或直流电平等信号的波峰因数为 2。其他波形本质上更复杂,具有更高的波峰因数。正弦波的波峰因数为 1(即 4142.1)。因此,均方根电平为2 V的正弦波的峰峰值幅度为8284.<> V。
信号幅度测量技术
I 二极管检测
图3所示为常用二极管检测电路的原理图。这是一个具有输出滤波功能的简单半波整流器。输入端的 68 电阻产生标称 50 输入匹配。
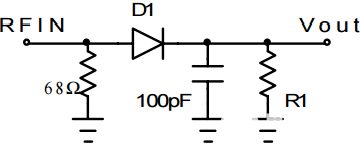
图 3: 一个简单的二极管检测器 2
图4显示了输出电压与输入信号的函数关系,单位为dBm。
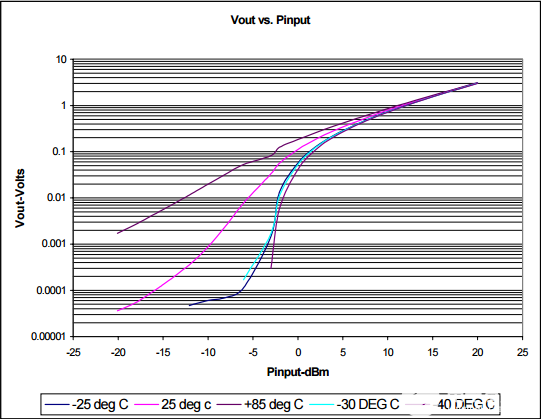
图 4:简单二极管检波器电路的 Vout 与引脚
虽然该电路在25°C时的传递函数是合理的线性,但在低输入电平和整个温度范围内性能会显著下降。图5显示了一个经过改进的二极管检波器电路,该电路包含一些温度补偿。在该电路中,二极管电压的温度依赖性由第二个二极管补偿。因此,当D1两端的压降随温度升高时,D2两端的电压保持不变。这使电阻分压器中心的电压保持恒定,分压器用作输出。
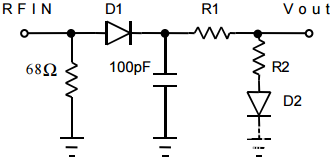
图 5: 温度补偿二极管检测器 2
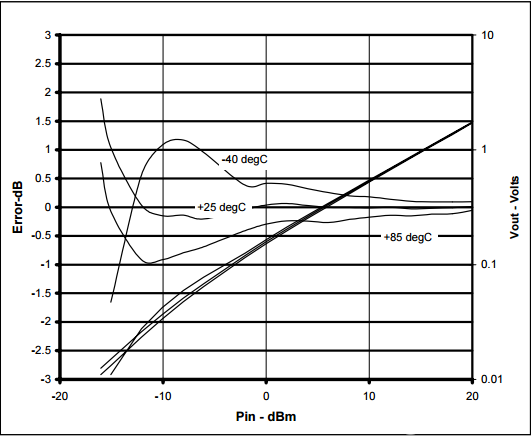
图6:温度补偿二极管检测器的Vout和误差与引脚的关系
图6显示了该温度补偿电路的传递函数。为了仔细研究改进的线性度和温度稳定性,线性回归可以计算这些点的最佳直线拟合;也就是说,一个方程的形式,

请注意,为了进行此计算,有必要将以dBm为单位的功率数转换为电压(电压输入/电压输出传递函数给出名义上的线性关系)。使用这条理想的直线,我们可以绘制响应在其动态范围内的线性度。在实际应用中,我们希望在室温下校准电路,而不是在温度下校准电路。因此,我们计算在室温下测量的最佳直线随温度变化的误差。这为我们提供了该解决方案的系统级精度的良好衡量标准。
图6显示,温度补偿二极管检波器在高功率水平下具有良好的温度稳定性,但在低输入电平时仍然变得温度稳定性降低,线性度降低。需要注意的是,电路的输出不能加载任何显著的电阻。在低温下,该电路具有极高的输出阻抗。事实上,驱动小于FET缓冲放大器的任何东西都会导致温度补偿算法失效,从而产生类似于图4的性能。
二极管检波器电路不测量真均方根信号强度,即使输入均方根信号强度保持不变(波峰因数越高,输出电压越低),这些检波器的输出电压也会随输入信号波峰因数而变化。然而,在信号具有恒定波峰因数的系统中,只要探测器已正确校准,这可能无关紧要。因此,例如,如果无线电链路仅使用一种调制方案(例如QPSK),则可以进行精确的功率测量。然而,在具有不同波峰因数的系统中,例如CDMA或WCDMA,真正的均方根测量变得困难。此问题的一个解决方案是根据基站中的呼叫负载使用不同的查找表(特定信道中的呼叫加载会改变波峰因数)。但是,这需要为每个呼叫加载场景校准基站。在多载波系统中,问题变得更加严重,其中多个载波的波峰因数彼此独立地变化。
二、热检测
热检测本质上涉及我们之前研究的均方根经典定义的实际实现。这是理论上最简单的真均方根测量技术;然而,在实践中,实施起来既困难又昂贵。它涉及将未知交流信号的热值与已知校准直流参考电压的热值进行比较(见图7)。当校准的基准电压调整为使基准电阻(R2)和信号电阻(R1)之间的温差为零时,这两个匹配电阻的功耗将相等。因此,根据均方根的基本定义,直流基准电压的值将等于未知信号电压的均方根值。
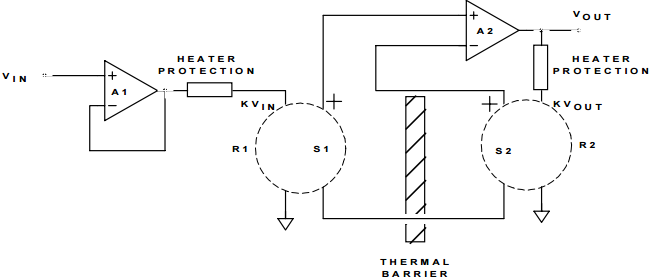
图 7: 热检测
每个热单元包含一个稳定的低TC电阻器(R1,R2),该电阻器与线性温度电压转换器(S1,S2)热接触,例如热电偶。S1/S2的输出电压与Vin的均方成比例变化;一阶温度/电压比随K Vin/R1而变化。
图7所示电路通常具有非常低的误差(约0.1%)和宽带宽。然而,热量单元(R1S1、R2S2)的固定时间常数限制了该均方根计算方案的低频有效性。
除了这种基本类型之外,还有可变增益热转换器可用,可以克服固定增益转换器的动态范围限制,但代价是增加复杂性和成本。
审核编辑:郭婷
-
USB射频功率计-购线网2017-07-05 0
-
功率概念和功率测量2017-09-22 0
-
【转帖】浅析射频功率测量方法2018-04-28 0
-
基于功率分析仪的802.11ac射频测量2019-06-06 0
-
射频功率的测量方法2019-06-24 0
-
射频功率测量经验总结2019-07-17 0
-
射频功率的频域测量是最基本的测量2019-07-23 0
-
射频功率的频域测量怎么避免误差?2019-10-08 0
-
NRP2 回收 射频功率计2019-10-12 0
-
基于对数检测法的射频功率测量电路设计2011-12-22 1886
-
射频必做实验3_无源射频器件的测量:功率分配器2016-06-29 714
-
射频功率测量技术2017-08-02 987
-
射频功率的测量和控制(第三部分)2023-02-03 1177
-
失配损耗对射频功率测量和级联放大器增益的影响是什么2023-02-19 1855
全部0条评论

快来发表一下你的评论吧 !

