触发器的原理和应用

文章来源：APC科学联盟

原文作者：APC君

要提到计算机的工作原理，就不得不提到一种电子装置：触发器。触发器主要由两个电子管组成，当电流通过触发器时会通过其中一个电子管。触发器一共有四个接触点，其中两个用来接收外部脉冲，另外两个用来输出回答脉冲。外部脉冲输入的瞬间，触发器就会“翻转”，使原本导通的电子管变成闭合状态，电流转而进入另一个电子管。当一边电子管闭合、另一边电子管导通的瞬间，触发器就会输出回答脉冲。

现在我们给触发器连续不断地输入脉冲，并根据图1中两根电子管其中的一根——右侧的电子管的状态来确定触发器的状态：当右侧电子管闭合时，设定触发器是「0 状态」；当右侧电子管导通时，设定触发器是「1 状态」。

如果触发器的初始状态为「0 状态」，即右侧电子管为闭合状态时（如图 1所示），那么输入第一个脉冲后，右侧电子管导通，触发器翻转成「1 状态」。此时，触发器不会输出回答脉冲，因为左侧电子管并未导通。接下来，当我们输入第二个脉冲时，左侧电子管导通，右侧电子管闭合，触发器翻转为「0 状态」，输出回答脉冲。

通过观察可以发现，经过两次输入脉冲之后触发器回到了原始状态。接着继续输入第三个脉冲，触发器变成了「1 状态」，再输入第四个脉冲，触发器又变成「0 状态」……也就是说，触发器的状态是以2个脉冲为周期进行循环的。

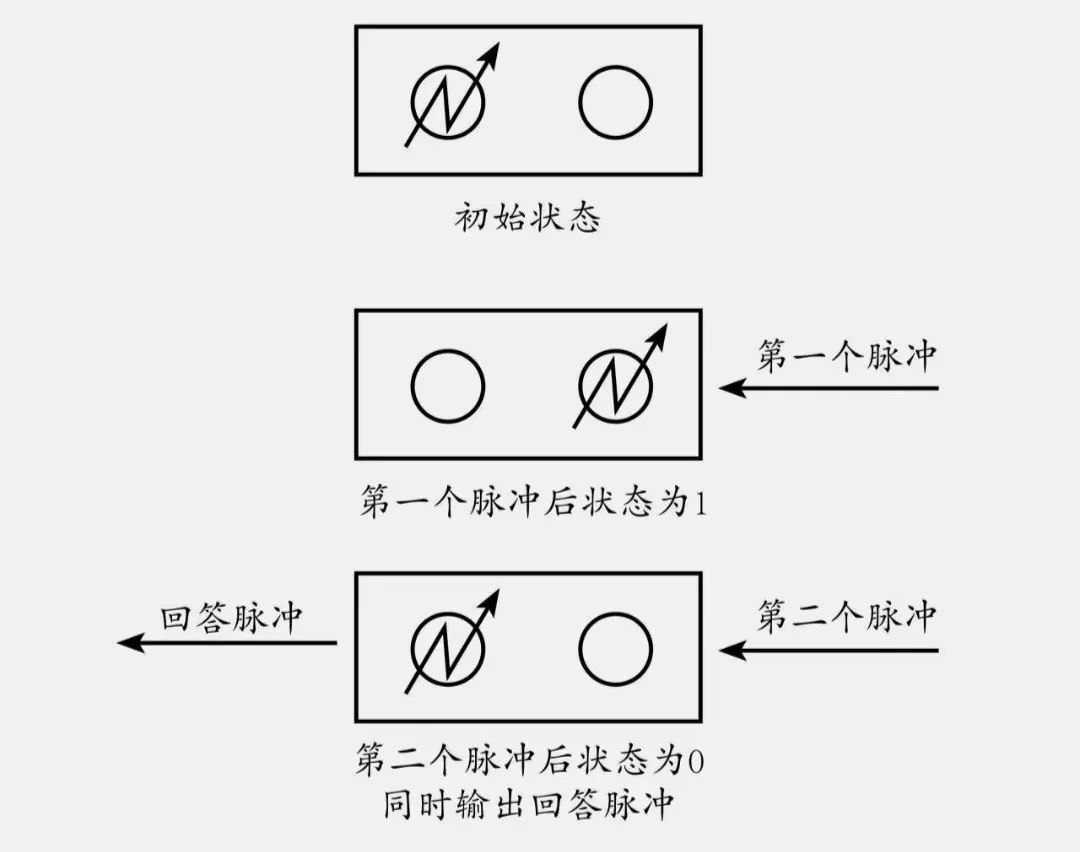
图1

如果将多个触发器相互连接会发生什么事呢？以三个触发器：触发器1、触发器2、触发器3相连为例（如图 2 ），给触发器1输入脉冲信号，之后触发器1的回答脉冲会作为触发器2的输入脉冲，触发器2的回答脉冲之后又会作为触发器3的输入脉冲，最后触发器3产生回答脉冲。 

图2

假设一共有 5 个触发器相互连接，最初的状态都为「0 状态」，我们可以把这个触发器组的状态标记为「00000」。给最右边的触发器输入第一个脉冲后，该触发器的状态变为「1 状态」，但由于没有回答脉冲，左侧的 4 个触发器依旧是「0 状态」，整体可以标记为「00001」。接着，我们输入第二个脉冲，最右边的触发器翻转为「0 状态」，同时最右边的触发器输出的回答脉冲输入相邻的触发器中，相邻的触发器翻转，成为「1 状态」，其他触发器由于没有接收到回答脉冲，仍旧处于「0 状态」，整体可标记为「00010」。紧接着输入第三个脉冲，最右边的触发器又会翻转为「1 状态」同时不输出回答脉冲，其他触发器状态不变，状态为「00011」。如此循环，我们最终得到如下数据：

输入第 1 个脉冲后的状态为：00001

输入第 2 个脉冲后的状态为：00010

输入第 3 个脉冲后的状态为：00011

输入第 4 个脉冲后的状态为：00100

输入第 5 个脉冲后的状态为：00101

输入第 6 个脉冲后的状态为：00110

如果把上述状态视为二进制的数字，转换为十进制之后我们就能依次得到1，2，3，4，5，6，…。由此可见，相互连接的触发器可以对外部脉冲信号进行「计数」，而且是一种特殊的计数方式。

二进制通过「0」和「1」来表示所有数字。与十进制有所不同的是，二进制的后一位是前一位的 2 倍，而不是 10 倍。二进制数转化成十进制数时，将每位数分别乘以2 的 n 次方（ n 代表位数）并求和即可。例如，将二进制数「10011」转化为十进制，就是 1 × 2^0 + 1 × 2^1 + 0 × 2^2 + 0 × 2^3 + 1 × 2^4 = 19。

触发器每翻转一次（也就是每输入一个脉冲信号），只需要一亿分之几秒的时间。现代计数触发器可以在 1 秒之内「计算」1000 多万个脉冲，而人眼需要 0.1 左右秒才能识别变换的信号。可以说，跟人类相比，它快了将近 100 万倍。

下面，我们来看看触发器如何进行加法运算。把三排触发器按照图 3 所示连接起来，其中第一排触发器用来表示被加数，第二排触发器用来表示加数，第三排触发器则用来表示二者之和。当上面两排触发器的状态为「1」时，会分别向第三排触发器输出脉冲信号。

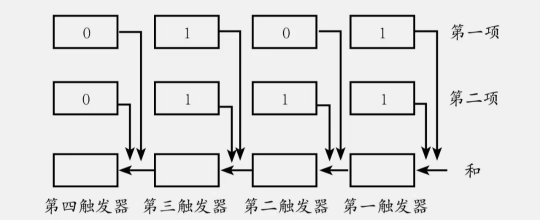
图3

图3的例子中，前两排触发器记下的两个二进制数是 101 和 111。第三排的第一触发器从前两排的第一触发器处别得到一个脉冲信号（一共得到两个脉冲信号），根据前面的分析，第三排的第一触发器依旧处于「0 状态」，同时会给第三排的第二触发器输出一个回答脉冲。除了这个回答脉冲之外，第三排的第二触发器还会从第二排的第二触发器得到一个回答脉冲，一共得到两个脉冲信号，处于「0 状态」，并输出一个回答脉冲给第三排的第三触发器。除了这个回答脉冲之外，第三排的第三触发器还从第一排和第二排各得到一个脉冲，共得到 3 个脉冲，状态为「1」，同时输出一个回答脉冲。第三排的第四触发器只得到这一个回答脉冲，状态为「1」。以上过程就是二进制数的加法运算，如果写成竖式运算，就如下图所示：

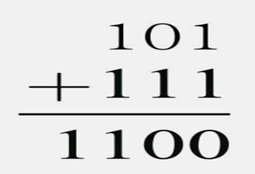
图4

将图4中的二进制数换算为十进制数，就会得到 5 + 7 = 12。第三排触发器输出的回答脉冲相当于竖式加法运算的进位。如果每排的触发器有 20 个（或者大于 20 个），就可以计算百万级甚至千万级数的加法。如果把上述方案改造一下，不但可以进行加减法运算，还可以进行乘法运算和除法运算。

审核编辑：汤梓红