

自动驾驶:自动泊车之AVM环视系统算法2
描述
本文的内容主要讲述AVM 3D算法pipeline,一种自研提取角点标定方法,汽车辅助视角。每个部分都涵盖了完整的算法理论以及部分代码,适合有一些计算机视觉基础的同学,或许可以给相关方向的同学做些参考。
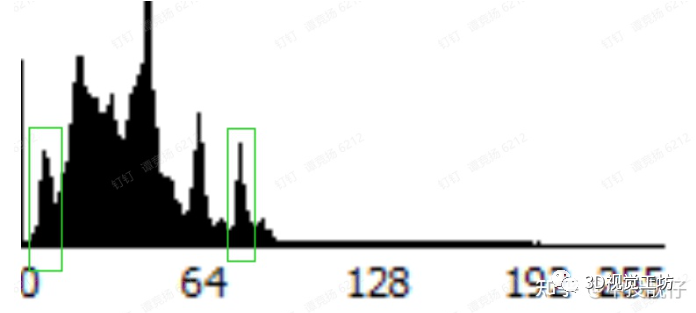
·双峰自适应阈值二值化大体思路为:计算图像的亮度直方图。分别计算暗区局部极大值,亮区局部极大值,即“双峰”。计算双峰亮度的平均值,作为阈值,来对图像做二值化。因此称为“双峰自适应阈值”。
·使用上述约束条件筛选出大方格的角点。综上,使用这种方法提取出的角点分布得更广泛,且都在鸟瞰图的分布区域,因此拼接融合得效果更佳。 大部分车上的广角功能是对鱼眼图直接做了去畸变,这种方法带来的问题及产生原因如下:·放大上表中普通广角图,不难发现标定布前边缘并不是平直的,它有一定的倾斜。这是因为相机有一个roll翻滚角,相当于人眼没有水平正视前方,而是歪着脑袋看前面。·在远离图像中心的位置,像素被严重拉伸,这是透视畸变的一种(见附录),会导致即便是我们把去畸变图的分辨率调整到非常大,在这张图像上依然不能看到FOV范围很大的内容,如图所示。
大部分车上的广角功能是对鱼眼图直接做了去畸变,这种方法带来的问题及产生原因如下:·放大上表中普通广角图,不难发现标定布前边缘并不是平直的,它有一定的倾斜。这是因为相机有一个roll翻滚角,相当于人眼没有水平正视前方,而是歪着脑袋看前面。·在远离图像中心的位置,像素被严重拉伸,这是透视畸变的一种(见附录),会导致即便是我们把去畸变图的分辨率调整到非常大,在这张图像上依然不能看到FOV范围很大的内容,如图所示。
这个流程与上面的车轮视角的算法流程几乎是相同的,所有的相机位姿变换导致的视角转换都可以用这个流程来实现。在上面的相机位姿矫正示意图中我们可以看到,垂直于地面的墙、柱子的倾斜问题都解决了。被我们用基于相机位姿矫正的单应变换强行掰正了。但是,这个图在远离图像中心的边缘依然存在严重的拉伸。导致即使图像的分辨率很大,我们可以看到的实际FOV范围依然很小。针对这个问题,再一次进行平面的单应变换。·平面单应变换 广角与超广角实际的实现方法如下图所示,在广角图像上选取4个点(即远离图像中心在图像左右两边的两个小长方形),并设置这四个点做投影变换的结果(这4个点是通过大量实验调试出的一组最优超参数),使用这四对匹配点计算单应矩阵H。即计算将小长方形压缩成梯形的单应矩阵H。
广角与超广角实际的实现方法如下图所示,在广角图像上选取4个点(即远离图像中心在图像左右两边的两个小长方形),并设置这四个点做投影变换的结果(这4个点是通过大量实验调试出的一组最优超参数),使用这四对匹配点计算单应矩阵H。即计算将小长方形压缩成梯形的单应矩阵H。
一. 一种更优的联合标定方案
1.1 算法原理分析
在前面的工作中,我们调用opencv函数findChessboardCorners提取图像上位于标定布中间的棋盘格角点,然后计算投影矩阵H。在SLAM 14讲中[1],计算H就是求解Ax=0这样一个问题。其原理就是构造一个最小二乘的形式,用奇异值分解的方式来计算一个误差最小的解。而为了逼近这个最小误差,可能造成除了棋盘格角点以外的其他像素值的投影误差很大。换句话说,由于棋盘格角点集中于鸟瞰图的中心很小的一部分区域,如果选择棋盘格角点进行H的计算,会导致只有棋盘格附近的区域能够进行准确的投影,远离该区域会有较大误差。类似于nn的训练数据过于局限,训练的模型过拟合了。这也就能够解释为什么在之前的工作中,我们的鸟瞰图拼接区域总是拼不齐,就是因为我们选择的角点远离拼接区域,计算出的投影矩阵H在拼接区域的投影误差太大。我们开发了一种基于自动提取角点算法的汽车标定方法,该方法可以提取标定布上拼接区域黑色方格的角点。如图所示:

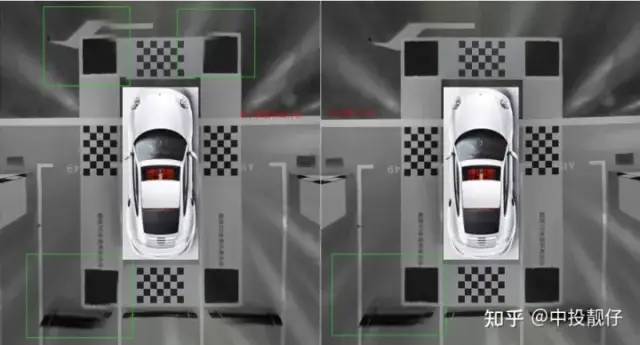
1.2 基于自动提取角点算法的汽车标定方法

|
1. 双峰自适应阈值二值化 2. 多边形检测 3. 四边形筛选 4. 提取四边形顶点 |

|
1. 多边形拟合结果必须为四边形,即筛选出二值化图中的四边形 2. 四边形面积必须大于某阈值(opencv源码中这个超参适用于筛选棋盘格的,我们要把这个阈值搞得大一些,用于筛选大方格) 3. 相邻边长不可相差过多 4. 选取黑色的四边形,而不是白色的四边形 5. 限制四边形分布范围,即四边形不能过于靠近图像边缘,具体情况与相机的位姿相关 |
二. AVM辅助视角——基于外参的视角变换
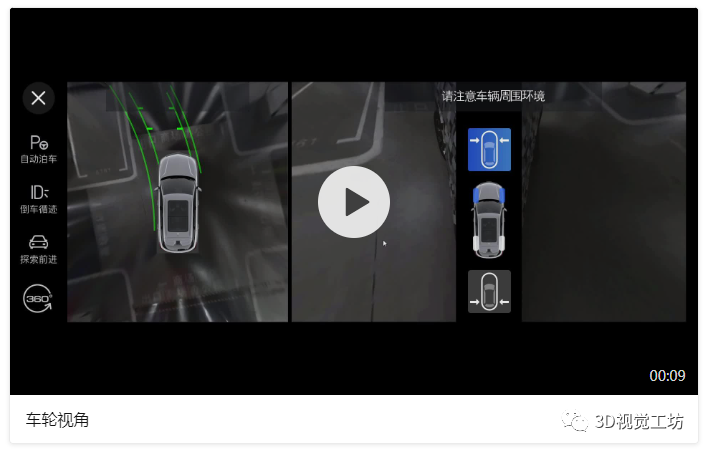
本章节主要讲述单应矩阵与PNP的原理,以及它们在AVM辅助视角中的实际应用,附带部分代码。关键词:单应矩阵、PNP、标定、广角、超广角、车轮视角、越野模式车载鱼眼相机可以获取到范围非常大的内容,但是鱼眼图像并不能够在汽车行驶过程中给驾驶员提供符合人类视觉习惯的视频图像,这一章节主要来讲述如何利用鱼眼相机的图像信息,来提供各种辅助视角。例如:(1)在进出车位或经过狭小空间时,驾驶员会更加关注车轮位置的内容,那么我们需要使用某种算法对左侧、右侧的鱼眼相机拍摄到的内容进行处理,得到“车轮视角”;
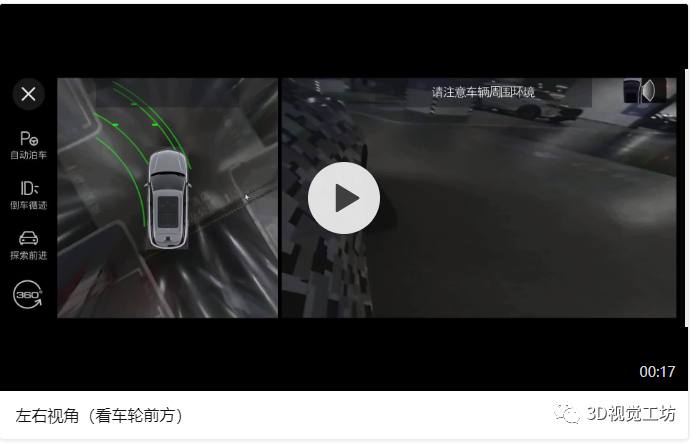

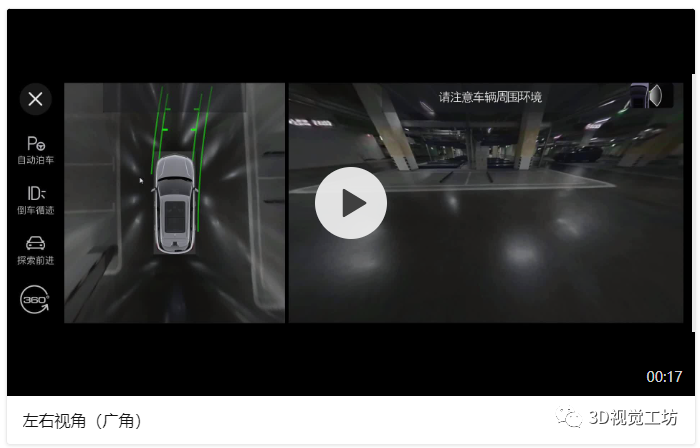
2.1 单应矩阵H的原理
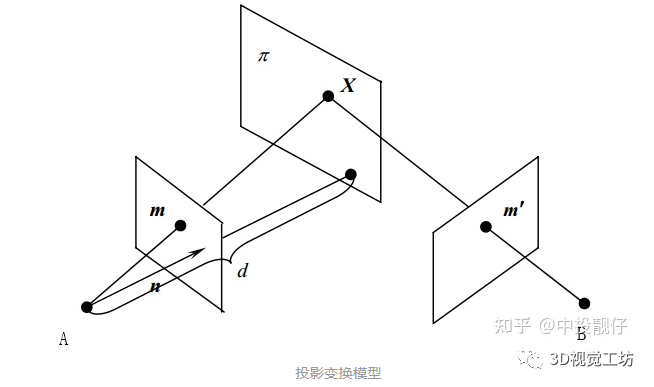
有CV基础的同学们大多知道单应矩阵表示“一个平面到另外一个平面的变换关系”。这样的描述是不准确的,或者如果对单应矩阵仅能说出这些,说明对单应矩阵的认识是片面的。正确的理解应该是:H描述的是在不同位姿下的两个相机cam1,cam2拍摄同一个平面(例如标定板),这个平面在两个相机成像平面上的成像结果之间的变换关系。投影变换模型图如下。以上这段话,被很多人简单理解成了“H描述的是两张图象之间的变换关系”,这里有两个点需要注意:(1)不要忽略掉了前面那部分和相机投影相关的物理模型(2)H描述的是空间中的某个平面分别在两个相机图像平面上的成像结果之间的变换,而不是两个图像之间的变换。对于单应矩阵,我们可以思考一个问题:我们拍摄到的内容,大多数情况下不仅仅包含某一个平面。而我们在做投影变换的时候,H就是基于某个平面计算出来的,这会导致虽然图像中的该平面部分的投影是合理的,但是因为平面以外的其他部分依然用相同的H做投影,这些部分的投影结果就会显得非常的奇怪。相信很多同学听说过一个结论:基于H的图像拼接方法,比较适用于视距较远的环境下。这是因为视距较远的环境下,拍摄到的景象我们可以近似认为它们在同一个平面上,那么我们基于这个平面计算出来的H,就几乎适用于整个图像中的内容。我们从最基础的相机物理模型来推导一遍单应矩阵H的公式,这样有利于我们更深入地理解。(本文仅推导这一个公式,通过物理模型对单应矩阵进行推导对后面的算法理解十分重要)如图所示,同一个相机在A,B两个位置以不同的位姿拍摄同一个平面:

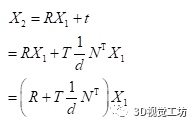
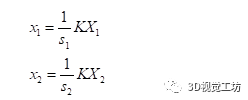
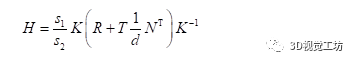
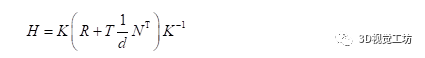
2.2 PNP的原理
用一句话概括PNP到底做了什么:已知相机A坐标系下的一组三维点,以及这组三维点在另外一个相机的图像坐标系下的二维坐标,就可以通过数学方法计算出A、B两个相机之间的位姿R,t。注意R,t是从A->B。公式如下:
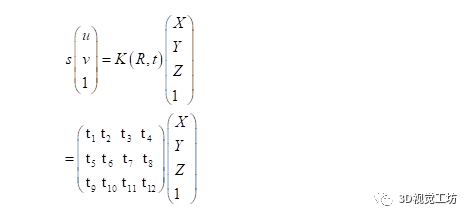
2.3 车轮视角

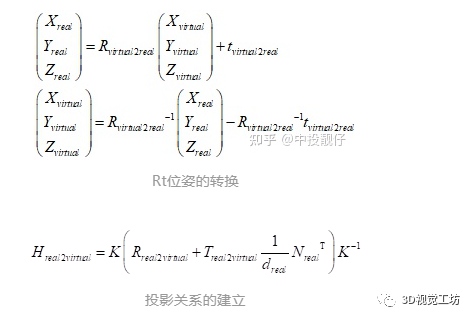
//函数定义 void solveRtFromPnP(const vector &corners2D, const vector &obj3D, const Mat &intrinsic, Mat &R, Mat &t) { Mat r = Mat::zeros(3, 1, CV_32FC1); solvePnP(obj3D, corners2D, intrinsic, cv::Mat(), r, t); Rodrigues(r, R); } //函数调用 solveRtFromPnP(corners_2D, obj_3D, m_intrinsic_undis, R, t); 以上,我们获取到了虚拟相机->真实部署相机之间的位姿R,t。至于R,t为什么不是从真实部署相机->虚拟相机,可以从PNP算法的公式推导中得知(前面已经讲过),或者见视觉SLAM第二版P180-P181。再回到投影变换H模型图中,图中的A就是虚拟相机,B就是真实部署相机。我们已经通过PNP计算出虚拟相机->真实部署相机的R,t。但是我们想要的是如何将真实相机拍摄到的某个平面(对于车轮视角而言是地面)通过H转换到虚拟相机的视角下。因此我们需要对R,t做一些处理,将其转化为真实部署相机->虚拟相机的位姿关系:公式推导:
//基于Rt计算H Mat solveHFromRt(const Mat &R, const Mat &t, const float d, const Mat &n, const Mat &intrinsic) { Mat intrinsic_inverse; invert(intrinsic, intrinsic_inverse, DECOMP_LU); Mat H = intrinsic * (R + t / d * n.t()) * intrinsic_inverse; return H; } PNP求解外参:/****************************************************************************************************************/ //R t:PNP算出的结果,从虚拟相机->真实部署相机的位姿 //计算出 真实部署相机->虚拟相机的位姿 Mat R_Camera2Real; invert(R, R_Real2Virtual, DECOMP_LU); Mat t_Real2Virtual = -R_Real2Virtual * t; //虚拟相机到地面的垂直单位向量 Mat n = (Mat_(3, 1) << 0, 1, 0); //真实部署相机到地面的垂直单位向量 n = R * n; // rotation float theta_X = m_wheel_sight_angle / 180.f * 3.14f; Mat R_virtual = (Mat_(3, 3) << 1, 0, 0, 0, cos(theta_X), -sin(theta_X), 0, sin(theta_X), cos(theta_X)); R_Camera2Virtual = R_virtual * R_Camera2Virtual; t_Camera2Virtual = R_virtual * t_Camera2Virtual; //计算单应矩阵H:真实视角->虚拟视角 Mat H = solveHFromRt(R_Camera2Virtual, t_Camera2Virtual, d, n, intrinsic); 几点说明:·n(0,1,0),说明单应矩阵选取的平面为地面。不要忘了我们最开始强调的,H描述的是在不同位姿下的两个相机cam1,cam2拍摄同一个平面(例如标定板),这个平面在两个相机成像平面上的成像结果之间的变换关系。因此这个平面的选择,对最终的投影结果有很大的影响。车轮视角选取地面作为我们要进行投影的平面,最终的效果非常nice。·代码中还包含rotation部分,这是因为我们在标定的时候让虚拟相机朝正前方,但显然理想的车轮视角相机应该朝向车轮,即应加一个俯仰角pitch。2.4 超级广角
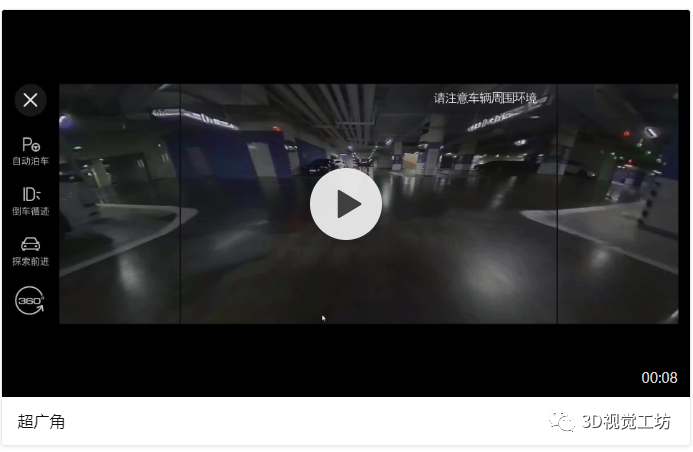
这部分我们是对标现有某德系车载超广角功能进行实现的,相比于直接做去畸变的广角效果,超广角的优势在于·纠正了相机翻滚角带来的视觉不适·纠正了左右两侧远离图像中心的拉伸效果·纠正了竖直方向由于透视畸变“近大远小”带来的柱体倾斜效果 大部分车上的广角功能是对鱼眼图直接做了去畸变,这种方法带来的问题及产生原因如下:·放大上表中普通广角图,不难发现标定布前边缘并不是平直的,它有一定的倾斜。这是因为相机有一个roll翻滚角,相当于人眼没有水平正视前方,而是歪着脑袋看前面。·在远离图像中心的位置,像素被严重拉伸,这是透视畸变的一种(见附录),会导致即便是我们把去畸变图的分辨率调整到非常大,在这张图像上依然不能看到FOV范围很大的内容,如图所示。
大部分车上的广角功能是对鱼眼图直接做了去畸变,这种方法带来的问题及产生原因如下:·放大上表中普通广角图,不难发现标定布前边缘并不是平直的,它有一定的倾斜。这是因为相机有一个roll翻滚角,相当于人眼没有水平正视前方,而是歪着脑袋看前面。·在远离图像中心的位置,像素被严重拉伸,这是透视畸变的一种(见附录),会导致即便是我们把去畸变图的分辨率调整到非常大,在这张图像上依然不能看到FOV范围很大的内容,如图所示。


| 1. 假设虚拟相机的位姿为朝向正前方,光轴与正前方的那面墙垂直,坐标系x、y、z如上表中“位姿校正的广角”所示 2. 标定出地面上那些角点在虚拟相机坐标系下的三维坐标 3. 在真实相机拍摄的图像中提取角点的图像坐标(实际上在第一章的标定过程中已经完成) 4. PNP计算虚拟相机->真实相机的位姿 RT 5. 计算真实相机->虚拟相机的位姿rt 6. 我们选定的是垂直于相机光轴的平面,计算这个平面从真实相机->虚拟相机的单应矩阵H,在我们的算法中,这个平面距离相机的距离d=10m,这是一个经验值。 |
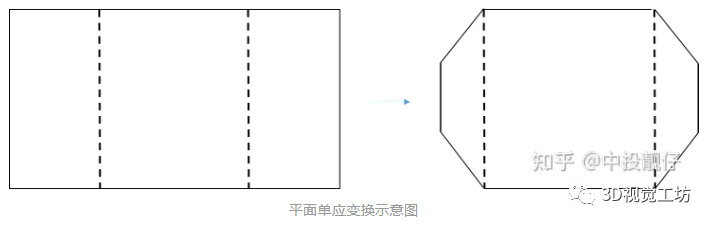
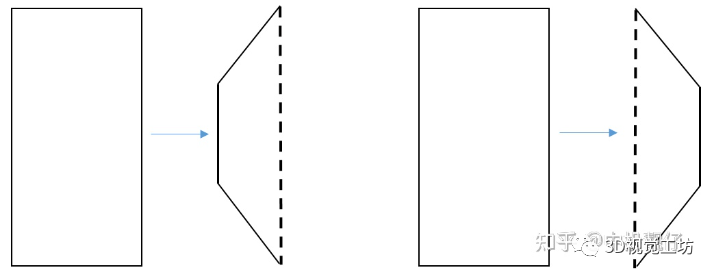
 广角与超广角实际的实现方法如下图所示,在广角图像上选取4个点(即远离图像中心在图像左右两边的两个小长方形),并设置这四个点做投影变换的结果(这4个点是通过大量实验调试出的一组最优超参数),使用这四对匹配点计算单应矩阵H。即计算将小长方形压缩成梯形的单应矩阵H。
广角与超广角实际的实现方法如下图所示,在广角图像上选取4个点(即远离图像中心在图像左右两边的两个小长方形),并设置这四个点做投影变换的结果(这4个点是通过大量实验调试出的一组最优超参数),使用这四对匹配点计算单应矩阵H。即计算将小长方形压缩成梯形的单应矩阵H。
Mat H_left = getPerspectiveTransform(p_src_left, p_dst_left); Mat H_right = getPerspectiveTransform(p_src_right, p_dst_right);三. 基于外参的3D 纹理映射方法
单目相机是丢失了深度信息的,计算机图形学中经常会使用将纹理图映射到某个3D模型上的方法,呈现出一种伪3D的效果,即纹理映射。在AVM中,通常使用将相机捕捉到的图像当作纹理,以某种方式映射到 3D 碗状模型上以呈现出一种3D 环视的效果。下面详细讲述下算法实现:3.1 3D模型
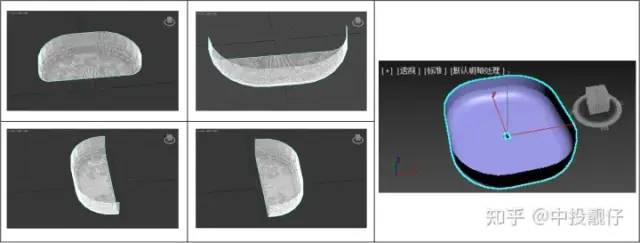
3.2 纹理映射
以前置相机为例,详细描述3D模型与相机图像之间的纹理映射关系:
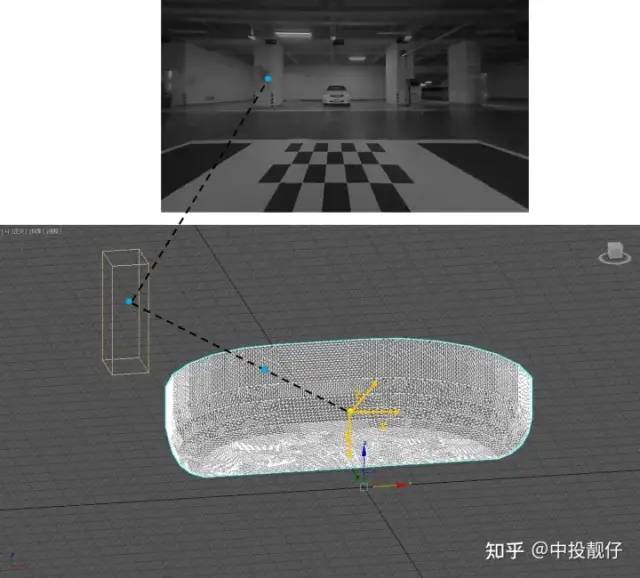
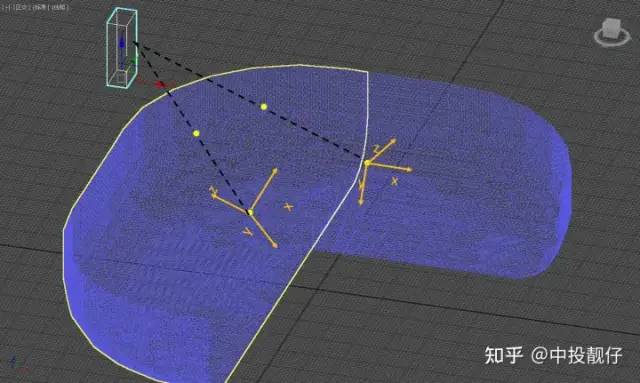
//calculate pose solveRtFromPnP(img_corners, obj_corners, intrinsic_undis, R, t); //3dsmax->camera Mat pts_3DsMax = (Mat_<float>(3, 1) << vertex[i].x, vertex[i].y, vertex[i].z); Mat camera_points = R * pts_3DsMax + t; //camera coordinate ->img coordinate Mat coor = intrinsic_undis * camera_points / camera_points.at<float>(2, 0); 上述代码将解析出来的3dsmax坐标系下的 3d碗模型的顶点三维坐标转换到相机坐标系下,然后通过相机内参转换到图像坐标系。最终建立起3d碗模型与图像纹理之间的映射关系。算法流程如下:算法流程| 1. 标定3dsmax坐标系下 标定布上角点的三维坐标。(即车身中心为原点的车身坐标系) 2. 检测相机拍摄到图像中标定布上角点的图像坐标。(第一章中已标定) 3. 利用1、2的坐标信息,通过PNP计算出 3dsmax坐标系与相机坐标系之间的位姿关系 R,t 4. 解析3d碗状模型的obj文件 5. 将解析出来的3d碗状模型的顶点三维坐标,通过R,t转换到相机坐标系下 6. 通过内参将相机坐标系的坐标转换到图像坐标系,建立起3d模型与相机图像之间的纹理映射关系 |
3.3 融合
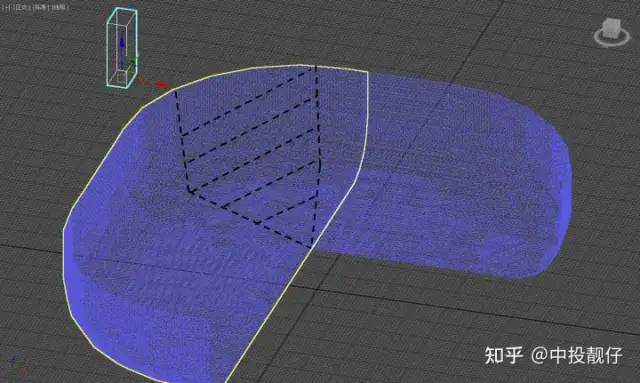
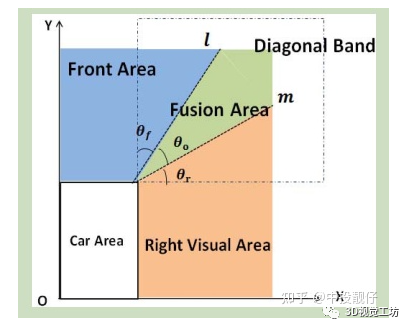
3.4 3D AVM算法存在的问题
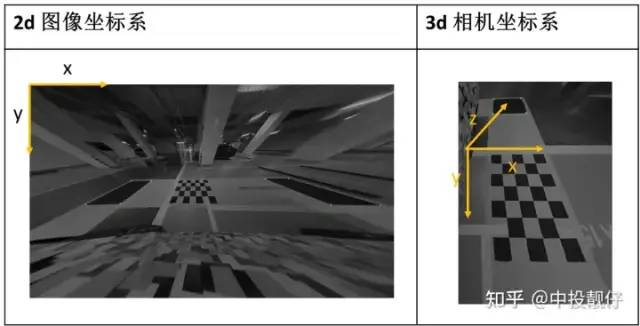
在讨论这个问题之前,我们首先要理解相机坐标系。相机坐标系一般x为朝右,y为朝下,z为朝向正前方。图中标记的两个坐标系分别为汽车前置摄像头、左侧摄像头的位姿。一个安装在汽车前方朝向前下方,一个安装在汽车左侧后视镜朝向左下方。
四 附录
透视畸变
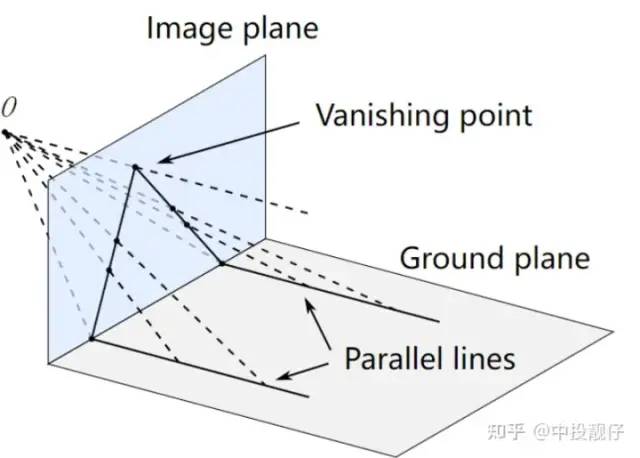
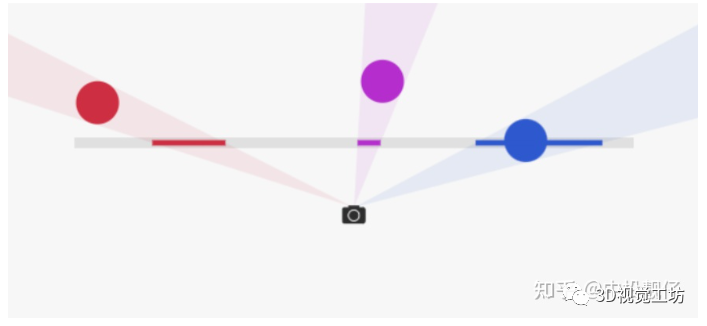
·“近大远小”“近大远小”表达的是:同一个物体,在远处的位置投影到相机平面上的大小要小于在近处的位置。例如,车道线投影到图像上并不是平行线,会交于一点。下图中O为相机原点,Image plane为相机成像平面,parallel lines为现实世界中两条平行线。这两条平行线投影到image plane上,距离相机越远的位置,其间距投影到image plane上的长度越短,最后汇聚到一点,即“消失点”。这个现象就类似于我们对图像做去畸变后,汽车前方两个垂直的柱子在图像中是斜的,最终会交于一点。但是如果相机光轴垂直于地面,车道线在图像上的成像结果就是平行的,类似于BEV。所以,我们在做超广角功能的时候,要对相机做位姿矫正,使相机的光轴朝向正前方,这样得到的图像结果中柱子就不会倾斜。
五 总结
本篇本章为avm系列的第二篇,至此AVM主要的算法原理已经讲述完毕,包含有:相机模型、相机内外参标定、相机联合标定方法、鱼眼去畸变、投影变换、光流、拼接融合、PNP、3D纹理映射、上帝视角、3d视角、广角、超广角、车轮视角等。后续还要做一些其他工作,例如:亮度一致调整、基于车道线的道路自标定、动态拼接线、相机模型优化等。希望以后还有机会和同学们交流,共同进步!审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
FPGA在自动驾驶领域有哪些应用?2024-07-29 8173
-
LabVIEW开发自动驾驶的双目测距系统2023-12-19 4390
-
基于自动泊车的自动驾驶控制算法设计与研究2023-05-04 1209
-
车辆自动驾驶技术之自动记忆泊车原理分析2023-02-05 2700
-
自动驾驶系统设计及应用的相关资料分享2021-08-30 2299
-
联网安全接受度成自动驾驶的关键2020-08-26 3061
-
自动驾驶汽车的处理能力怎么样?2019-08-07 2788
-
如何让自动驾驶更加安全?2019-05-13 3621
-
UWB主动定位系统在自动驾驶中的应用实践2018-12-14 3184
-
即插即用的自动驾驶LiDAR感知算法盒子 RS-Box2017-12-15 5979
-
自动驾驶的到来2017-06-08 7302
-
细说关于自动驾驶那些事儿2017-05-15 7014
-
自动驾驶真的会来吗?2016-07-21 14079
-
AVM全车监视系统 360度全景泊车系统2015-09-10 12453
全部0条评论

快来发表一下你的评论吧 !

