

基于反向传播PnP优化的端到端可学习几何视觉介绍
描述
摘要
深度网络在从大量数据中学习模式方面表现出色。另一方面,许多几何视觉任务被指定为优化问题。
为了将深度学习和几何视觉无缝地结合起来,至关重要的是进行端到端的学习和几何优化。
为了实现这一目标,我们提出了BPnP,这是一个新颖的网络模块,通过Perspective-nPoints(PnP)求解器反向传播梯度,以指导神经网络的参数更新。
基于隐式微分,我们表明一个 "独立的 "PnP求解器的梯度可以被准确有效地导出,就像优化器块是一个可微分的函数。
我们通过将BPnP纳入一个深度模型来验证它,该模型可以从训练数据集中学习相机的内在因素、相机的外在因素(姿势)和三维结构。
此外,我们开发了一个用于物体姿势估计的端到端可训练管道,该管道通过将基于特征的热图损失与二维-三维重投影误差相结合,实现了更高的准确性。
由于我们的方法可以扩展到其他优化问题,我们的工作有助于以一种原则性的方式实现可学习的几何视觉。
主要贡献
我们的主要贡献是一个名为BPnP的新型网络模块,它包含了一个PnP求解器。BPnP通过PnP "层 "反向传播梯度,以指导神经网络权重的更新,从而利用既定的目标函数(二维-三维重投影误差的平方和)和几何视觉问题的求解器实现端到端的学习。
尽管只结合了一个PnP求解器,我们展示了BPnP如何被用来学习有效的深度特征表征,用于多种几何视觉任务(姿势估计、运动结构、相机校准)。
我们还将我们的方法与最先进的几何视觉任务的方法进行比较。从根本上说,我们的方法是基于隐式微分的。
主要方法
反向传播的PnP算法: 让g表示一个 "函数 "形式的PnP求解器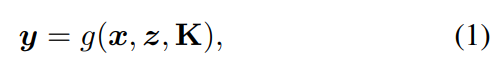
从n个2D-3D的对应关系中返回摄像机的6DOF姿态y和其内部参数K∈R3×3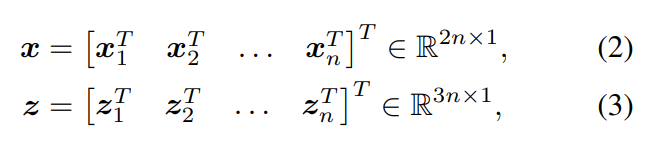
其中(xi , zi)是第i个对应关系。让π(-|y, K)是三维点在图像平面上的投影变换,姿态为y,相机本征为K。
从本质上讲,g的 "评估 "需要解决优化问题如下: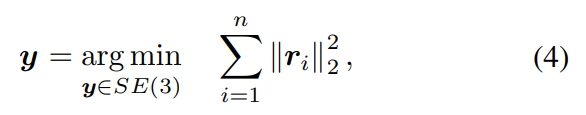
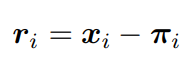
ri表示第i对对应关系的重投影误差。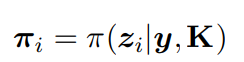
πi是三维点zi在图像平面上的投影。
我们的最终目标是将g纳入一个可学习的模型中,其中x、z和K可以是一个深度网络的(中间)输出。此外,公式(4)的求解器应该被用来参与网络参数的学习。为此,我们需要把g当作一个可微调的函数,这样它的"梯度 "就可以反向传播到网络的其他部分。接下来我们将详细介绍如何对反向传播的梯度进行计算。
1. 隐式函数定理(IFT) 这里简单公式推导了IFT隐式函数定理。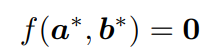
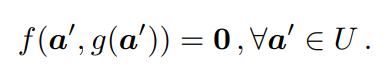
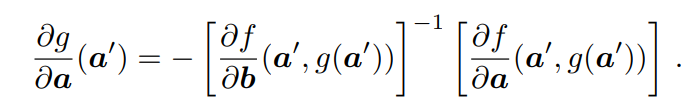
IFT允许计算一个函数g相对于其输入a的导数,而不需要函数的明确形式,但有一个函数f约束a和g(a)。
2. 构造约束函数f
为了调用隐式微分的IFT,我们首先需要定义约束函数f(a, b)。对于我们的问题,我们使用所有四个变量x、y、z和K来构造f。
但我们将f视为一个双变量函数f(a, b),其中a在{x, z, K}中取值--取决于要得到的偏导--而b=y(即g的输出姿势)。
为了维护约束函数f(a,b),我们利用了优化过程的静止约束。
在这里,将PnP求解器的目标函数g表示为: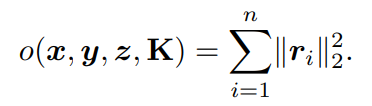
由于PnP求解器的输出姿态y是目标函数的局部最优,所以可以通过对目标的一阶导数与y的关系来建立一个静止约束,即: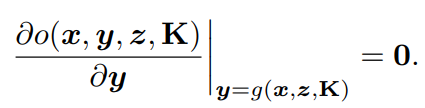
给出一个PnP求解器的输出姿势y = [y1, ..., ym] T,我们构建f,可以写为: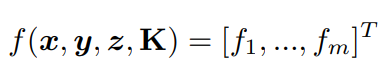
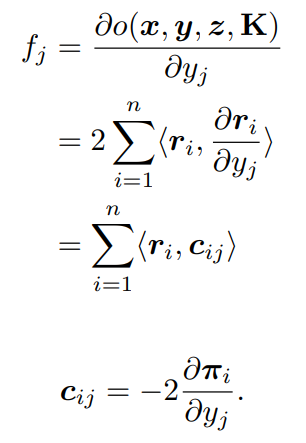
3. 前向和反向传播
我们对g的PnP公式基本上是执行最小二乘法(LS)估计,这对离群值(x、z和K的恶劣误差)并不稳健。
另外,我们可以采用一个更稳健的目标,如加入M-估计器[56]或使离群值的数量最大化[15]。
然而,我们的结果表明,LS实际上更合适,因为它对输入测量中的误差的敏感性鼓励学习快速收敛到不产生x、z和K中的异常值的参数。
相反,一个稳健的目标会阻止异常值的误差信号,导致学习过程不稳定。
鉴于(4),解算器的选择仍然存在。
为了进行隐式微分,我们不需要精确地解决(4),因为cij只是(4)的静止条件,任何局部最小值都能满足。
为此,我们采用Levenberg-Marquardt(LM)算法,该算法保证了局部收敛。
作为一种迭代算法,LM在求解(4)时需要初始化y(0)。
我们通过将(1)重写为:"(1)"来明确这种依赖关系: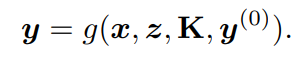
在反向传播中,我们首先构建f,然后得到g相对于其每个输入的雅可比系数,即: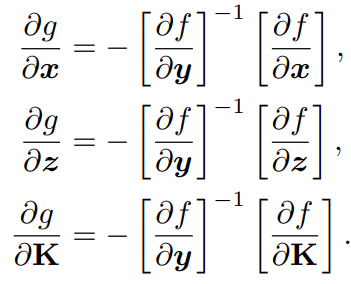
给出输出梯度,BPnP返回输入梯度: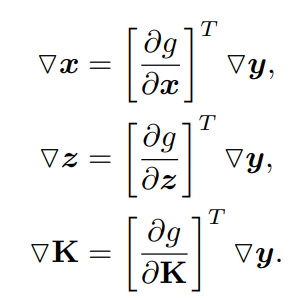
算法流程如下图所示:
主要结果: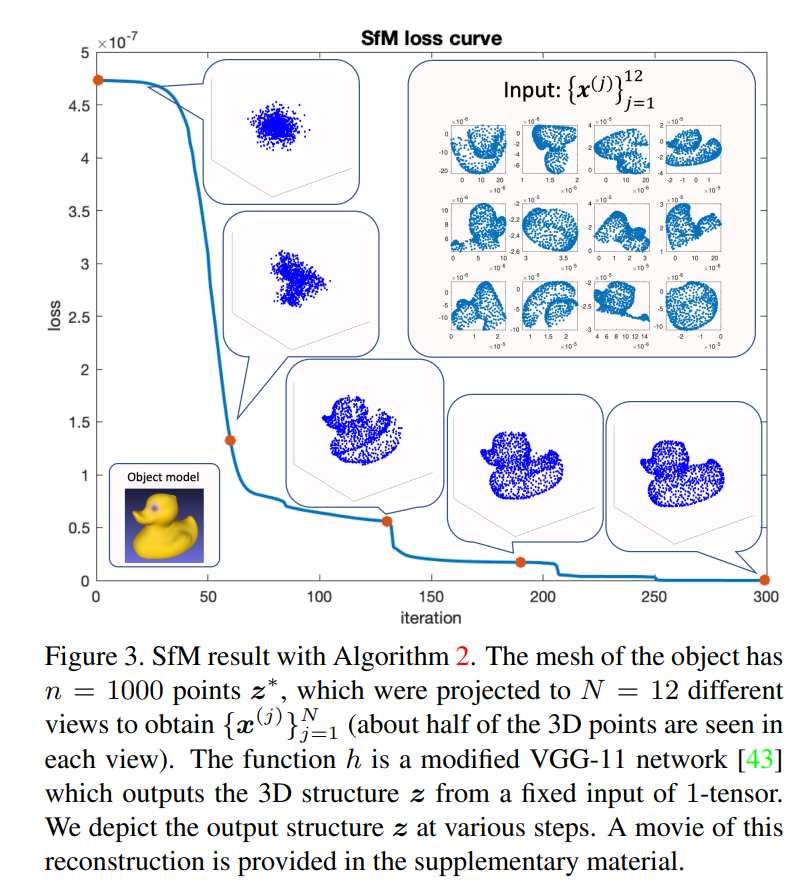
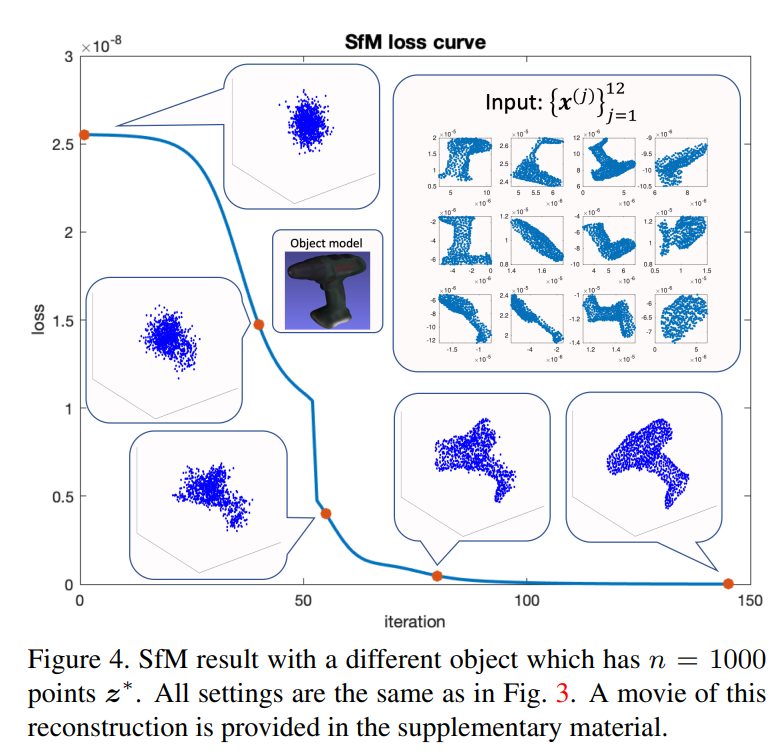
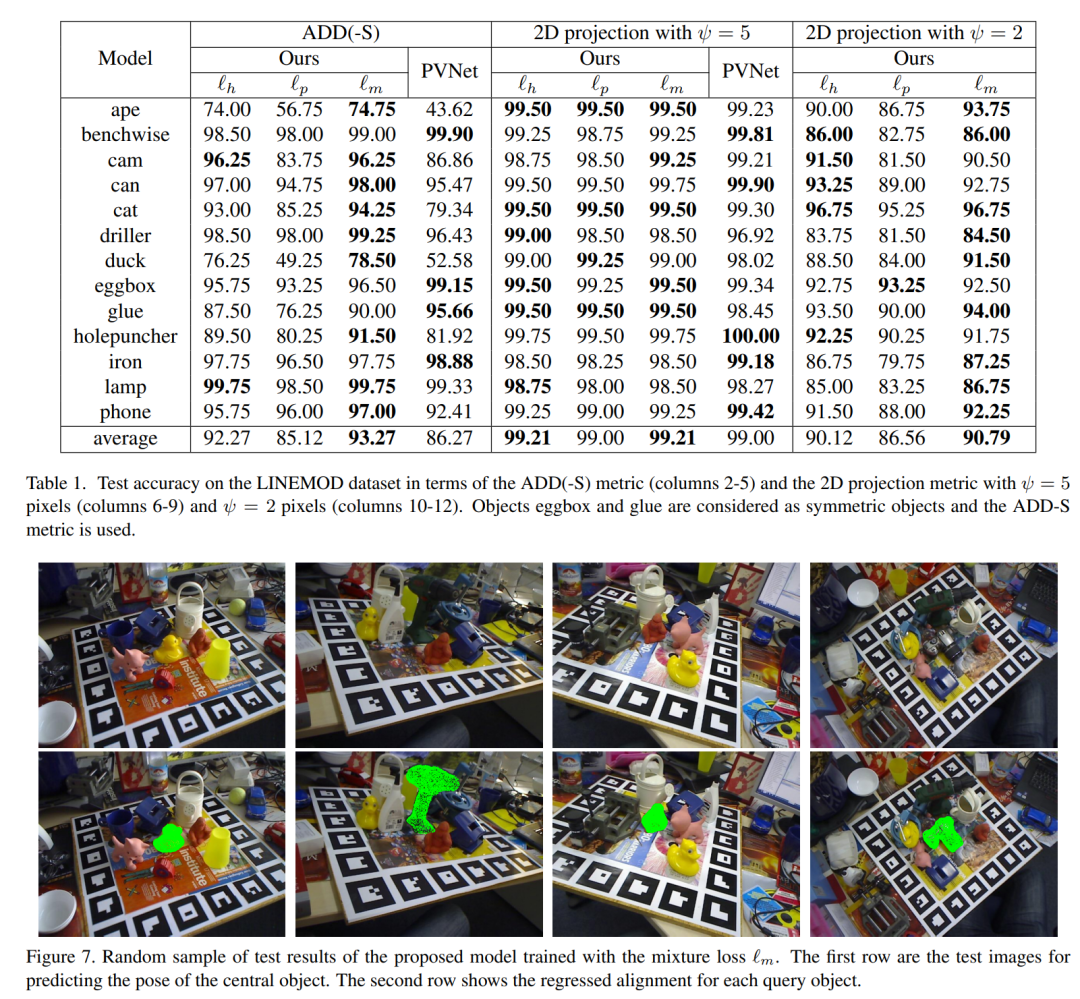
审核编辑:刘清
-
反向传播算法的工作原理2018-07-02 10670
-
深读解析反向传播算法在解决模型优化问题的方面应用2018-11-01 6419
-
端到端的自动驾驶研发系统介绍2019-07-13 6083
-
结合深度学习的自编码器端到端物理层优化方案2021-05-24 893
-
BP(BackPropagation)反向传播神经网络介绍及公式推导2021-07-26 1021
-
一种对红细胞和白细胞图像分类任务的主动学习端到端工作流程2022-08-13 1992
-
神经网络反向传播算法的优缺点有哪些2024-07-03 2665
-
连接视觉语言大模型与端到端自动驾驶2024-11-07 1181
-
什么是BP神经网络的反向传播算法2025-02-12 1395
全部0条评论

快来发表一下你的评论吧 !

