相控阵天线方向图：旁瓣和锥形

作者：Peter Delos, Bob Broughton, and Jon Kraft

介绍

在第1部分中，我们介绍了相控阵概念、声束控制和阵列增益。在第 2 部分中，我们介绍了光栅瓣和光束斜视的概念。在本节中，我们首先讨论天线旁瓣以及阵列逐渐变细的影响。锥形只是操纵单个元件对整体天线响应的幅度贡献。

在第1部分中，没有应用锥形，如图所示，第一个旁瓣为–13 dBc。锥形提供了一种以牺牲天线增益和主瓣波束宽度为代价来减小天线旁瓣的方法。在介绍锥形之后，我们将详细说明与天线增益相关的几点。

傅里叶变换：矩形↔正弦

在一个域中的矩形函数到另一个域中的sinc函数的转换在电气工程中以不同的形式出现。最常见的形式是矩形脉冲，在时间上，发出sinc函数的频谱内容。它也用于反向，其中宽带应用在时间上将宽带波形转换为窄脉冲。相控阵天线具有类似的特性：沿阵列平面轴的矩形加权辐射出遵循sinc函数的图案。

对于受此属性约束的应用，sinc函数的旁瓣存在问题，第一个旁瓣仅为–13 dBc。图 1 说明了这一原理。

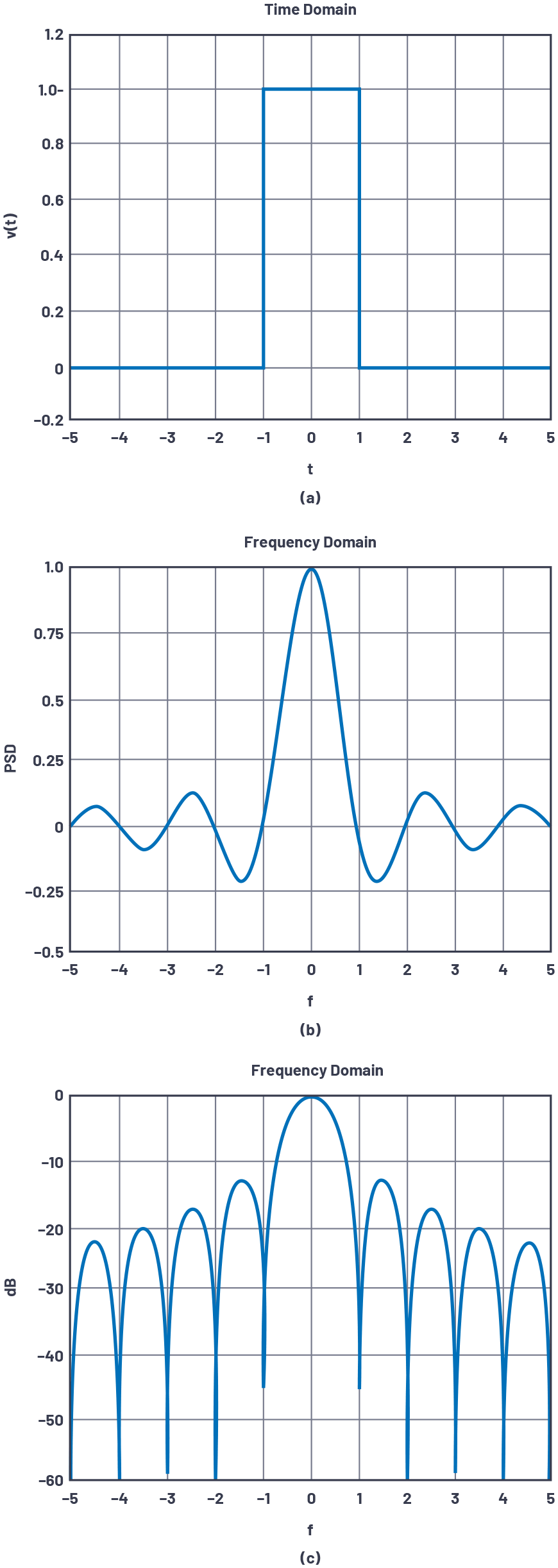
图1.时间上的矩形脉冲在频域中产生一个sinc函数，第一个旁瓣仅为–13 dBc。

逐渐变细（或加权）

旁瓣问题的解决方案是在矩形脉冲上施加加权。这在FFT中很常见，相控阵中的锥形选项直接类似于FFT中的加权。加权的不幸缺点是减少旁瓣的代价是扩大主瓣。一些示例加权函数如图 2 所示。

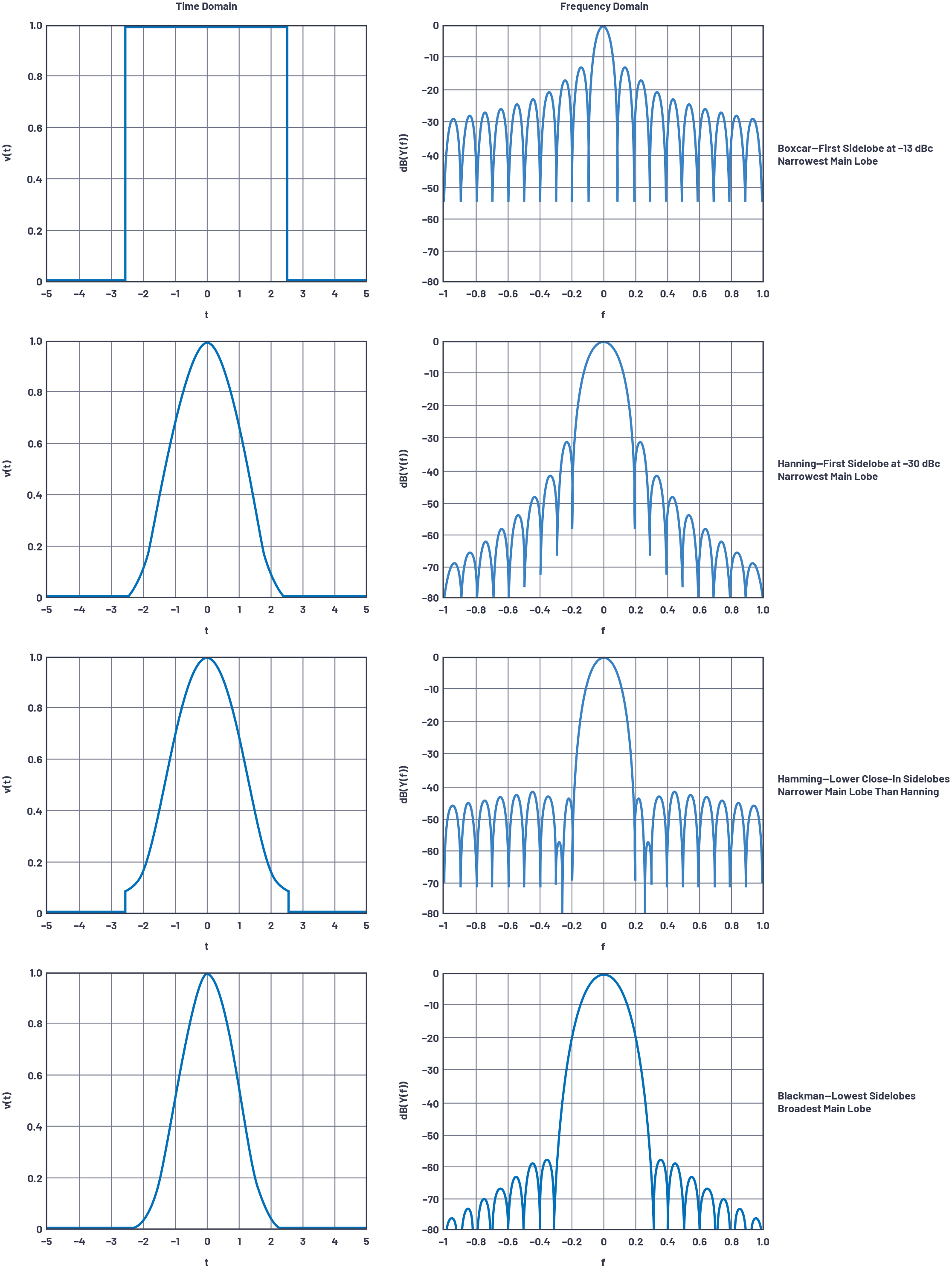
图2.加权函数示例。

波形与天线类比

从时间到频率的转换是常规的，以至于大多数电气工程师自然而然地可视化。然而，对于刚接触相控阵的工程师来说，如何使用天线模式的类比最初可能并不明显。为此，我们将时域信号替换为场域激励，并将频域输出替换为空间域。

时域→字段域

v（t） - 电压随时间变化

E（x） - 场强与孔径中位置的关系

频域→空间域

Y（f） - 功率谱密度与频率的关系

G（q） - 天线增益与角度的关系

图 3 说明了原理。在这里，我们比较了整个阵列中施加的两种不同权重的辐射能量。图3a和图3c说明了场域。每个点代表此 N = 16 数组中一个元素的振幅。在天线之外，没有辐射能量，辐射从天线边缘开始。在图3a中，场突然发生变化，而在图3c中，随着与天线边缘的距离逐渐增加。由此产生的对辐射能量的影响分别如图3b和图3d所示。

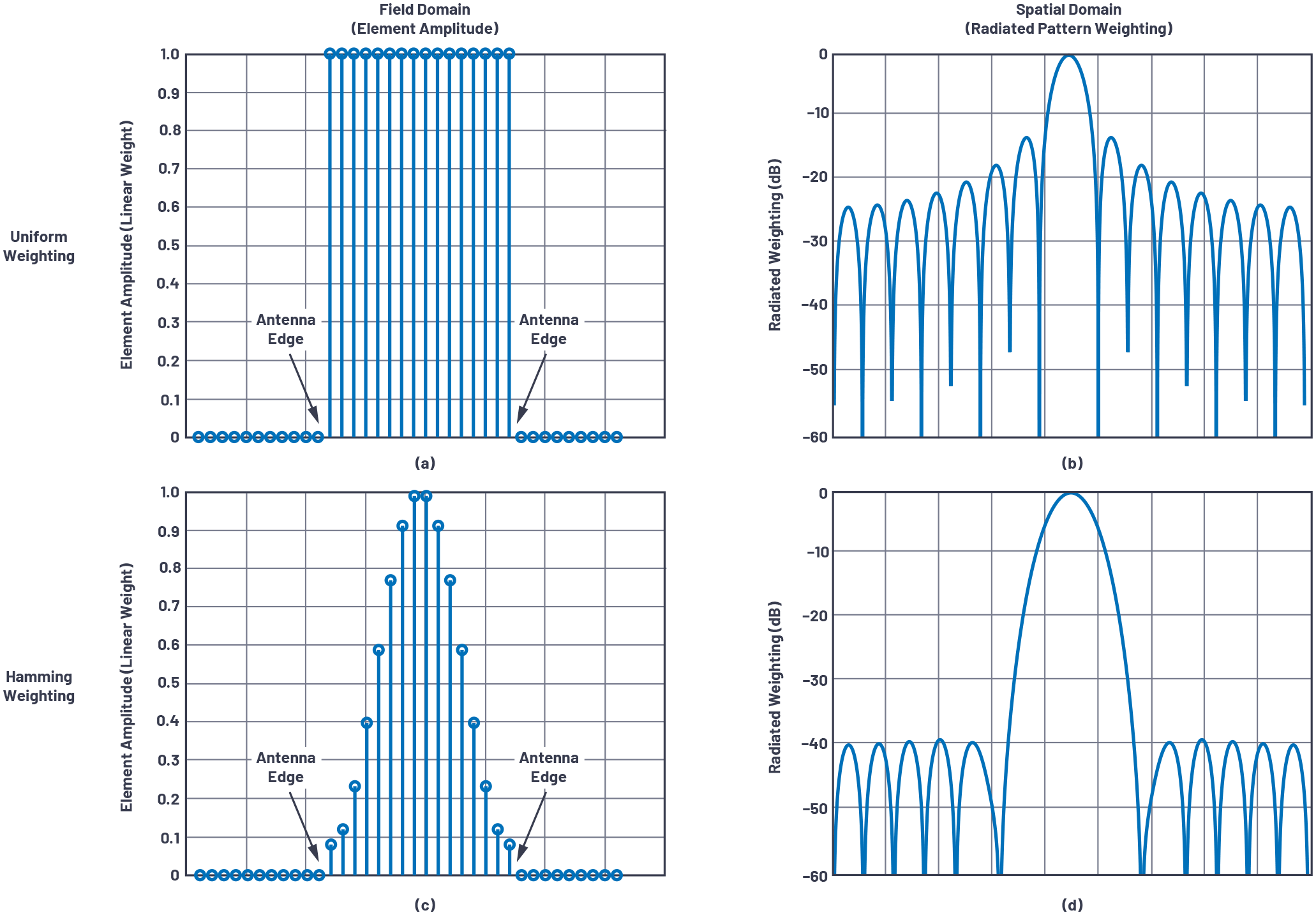
图3.显示元素逐渐变细转换为辐射能量加权的图表;（a） 对所有项目实行统一加权;（b） SINC 功能在空间上辐射;（c） 对各要素适用汉明加权;（d）辐射旁瓣降低到40 dBc，但代价是扩大了主光束。

在接下来的部分中，我们将介绍影响天线方向图性能的两个附加误差项。首先是相互耦合。就本文而言，我们仅承认用于量化影响的EM建模的问题和数量。第二个是量子化旁瓣，因为相移控制中的位数有限。对量化误差进行更深入的处理，并对量化旁瓣进行量化。

互耦误差

这里讨论的所有方程和阵列因子图都假设元素是相同的，并且每个元素具有相同的辐射方向图。实际上，情况并非如此。造成这种情况的原因之一是相互耦合，即相邻元素之间的耦合。当元素在阵列中广泛分离时，与间隔更近时，元素的辐射性能可能会发生显着变化。数组边缘的元素与数组中间的元素具有不同的周围环境。此外，随着光束的转向，元件之间的相互耦合会发生变化。所有这些效应都会产生一个额外的误差项，天线设计人员需要解释，在实践中，电磁模拟器花费了大量精力来表征这些条件下的辐射效应。

光束角分辨率和量化旁瓣

另一个实际的相控阵天线损伤是由于用于控制波束的时间延迟单元或移相器的分辨率有限。这通常是通过离散的时间（或相位）步长进行数字控制的。但是，如何确定实现光束质量目标所需的分辨率或位数呢？

与常见的误解相反，光束角分辨率并不等同于移相器的分辨率。在等式1（第2部分中的等式2）中，我们看到了这种关系：

我们可以用整个阵列的相移来表示这一点，方法是用数组宽度 D 代替元素间距 d。如果我们用移相器Φ LSB代替∆Φ，我们可以近似地获得光束角分辨率。对于N个晶片间隔为半波长的线性阵列，光束角的分辨率如公式2所示。

这是视线外的光束角分辨率，描述了当阵列的一半相移为零，另一半的相移器LSB相移时，光束角。如果阵列的一半不到一半编程到相位LSB，则可以获得更小的角度。图4使用30位移相器绘制了2晶片阵列的波束角，因为相位LSB在阵列中从左到右逐渐切换为晶片。请注意，光束角增加，直到一半的元件被LSB移动，然后当所有元件都在LSB处时返回零。这是有道理的，因为光束角通过阵列上的相位差异而变化。请注意，该特性的峰值为 θRES，如前所述。

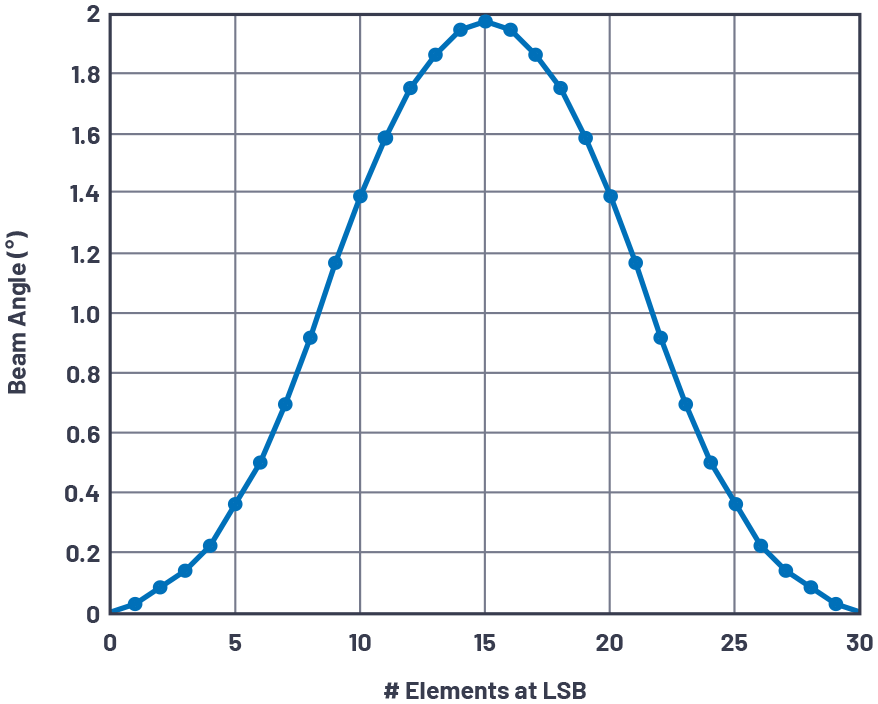
图4.30晶片线性阵列的LSB处的光束角与晶片数量的关系。

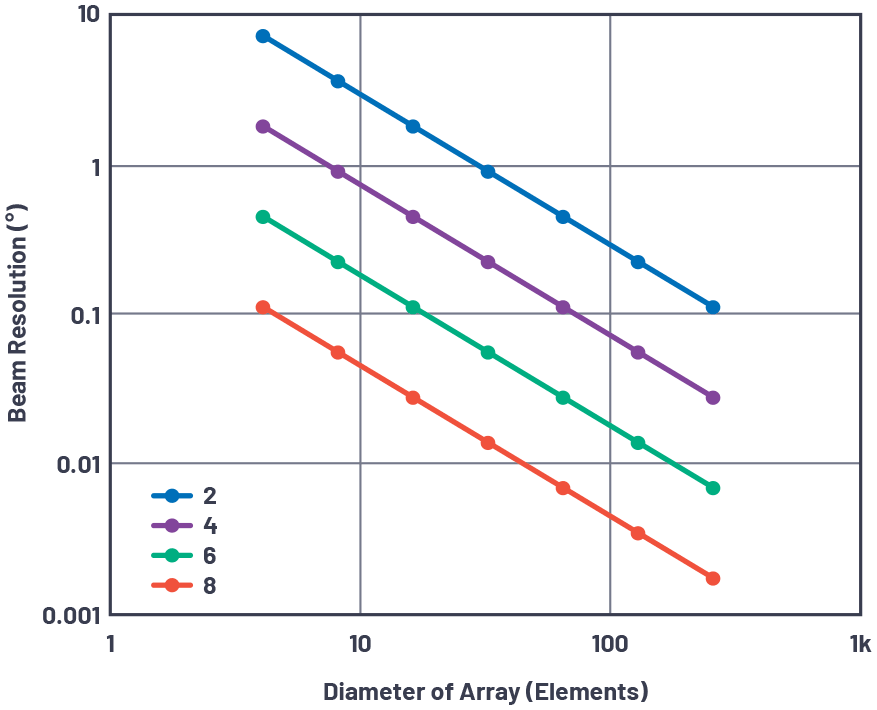
图5.2位至8位移相器分辨率的光束角分辨率与阵列尺寸的关系。

图 5 图 θRES作为不同移相器分辨率的阵列直径（λ/2晶片间距）的函数。这表明，即使是具有2° LSB的非常粗糙的90位移相器，对于1个晶片的阵列直径，也可以实现30°分辨率。求解第10部分中的方程1，对于间距为λ/30的2个晶片，主瓣波束宽度约为3.3°，这表明即使使用这种非常粗糙的移相器，我们也有足够的分辨率。那么，对于更高分辨率的移相器，我们能得到什么呢？根据时间采样系统（数据转换器）和空间采样系统（相控阵天线）之间的类比，更高分辨率的数据转换器产生的量化本底噪声更低。更高分辨率的相位/时移器导致更低的量化旁瓣电平（QSLL）。

图6显示了前面描述的2位30元件线性阵列的移相器设置和相位误差，编程为光束分辨率角θRES.阵列的一半设置为零相移，另一半设置为90°LSB。请注意，误差，理想和实际量化相移之间的差异是锯齿形的。

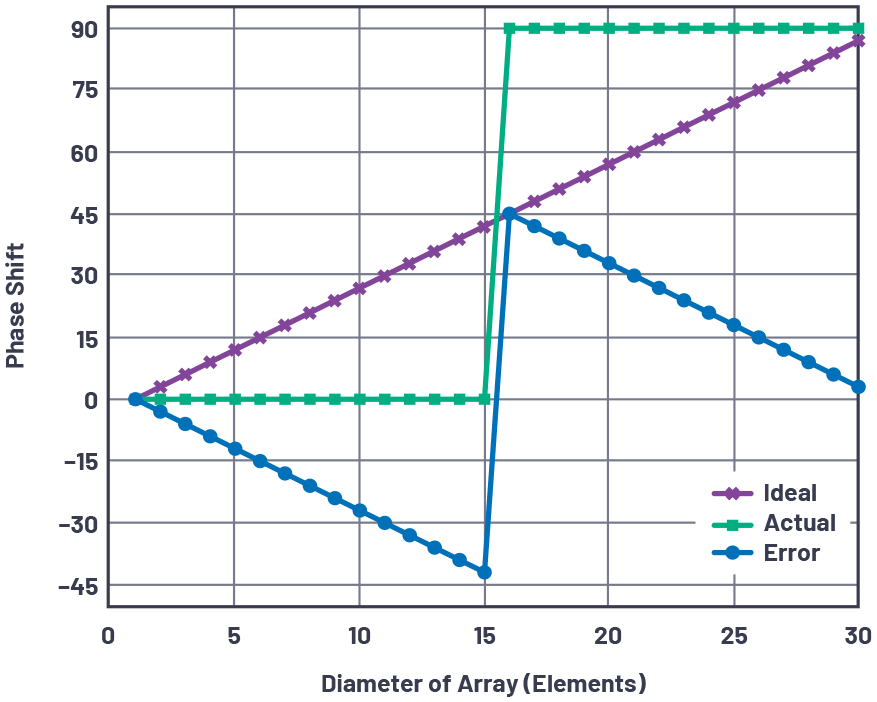
图6.阵列中的元素相移和误差。

同一天线转向至0°和波束分辨率角的天线方向图如图7所示。请注意，由于移相器的量化误差，图案会严重退化。

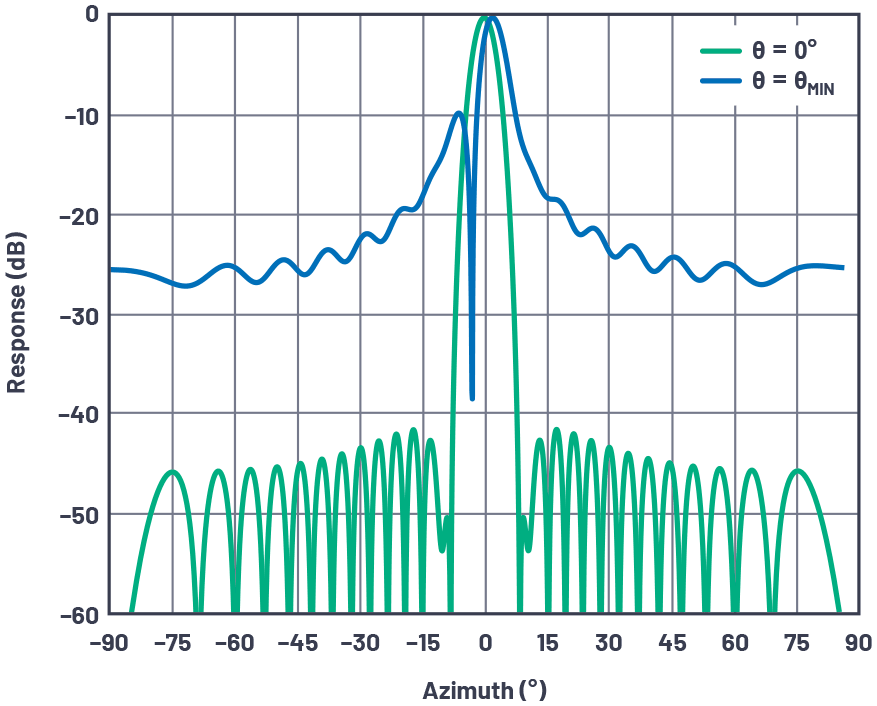
图7.具有最小波束角的量化旁瓣的天线方向图。

当最大量化误差发生在孔径上时，当其他元件的误差为零，而相邻晶片处于LSB/2时，就会出现最坏情况的量化旁瓣。这既表示最大可能的量化误差，也表示整个孔径上误差的最大周期性。图 2 中显示了 30 位、8 元件情况的这种情况。

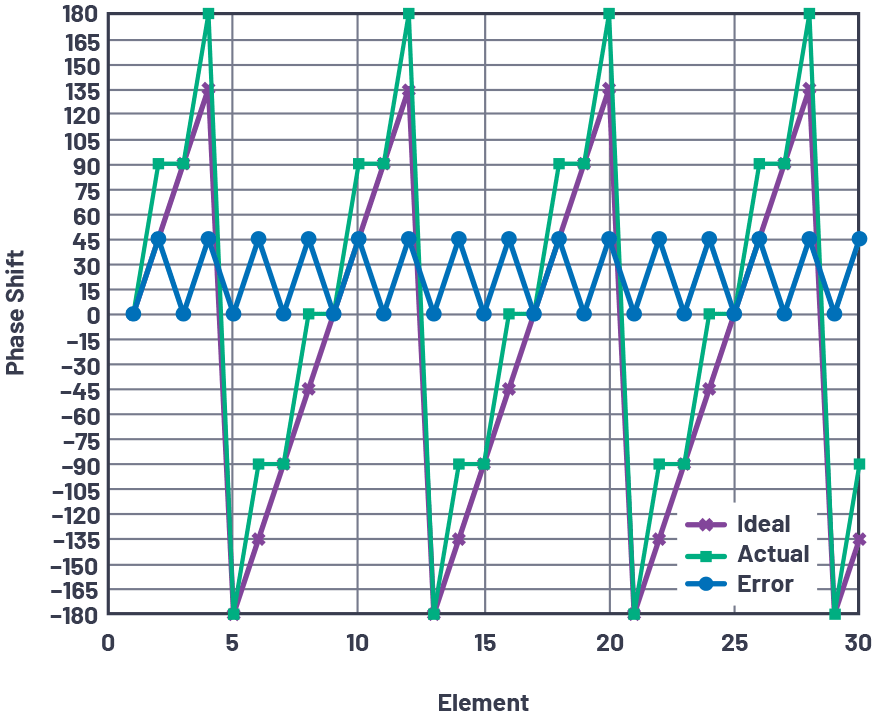
图8.最坏情况下天线量化旁瓣 - 2 位。

这种情况发生在可预测的光束角下，如公式3所示。

其中 n < 2位，n 是奇数。对于 2 位系统，此条件在视界之间满足四次，分别为 ±14.5° 和 ±48.6°。图9显示了该系统在n = 1，q = +14.5°时的天线方向图。请注意–7°处的大量–5.50 dB量化旁瓣。

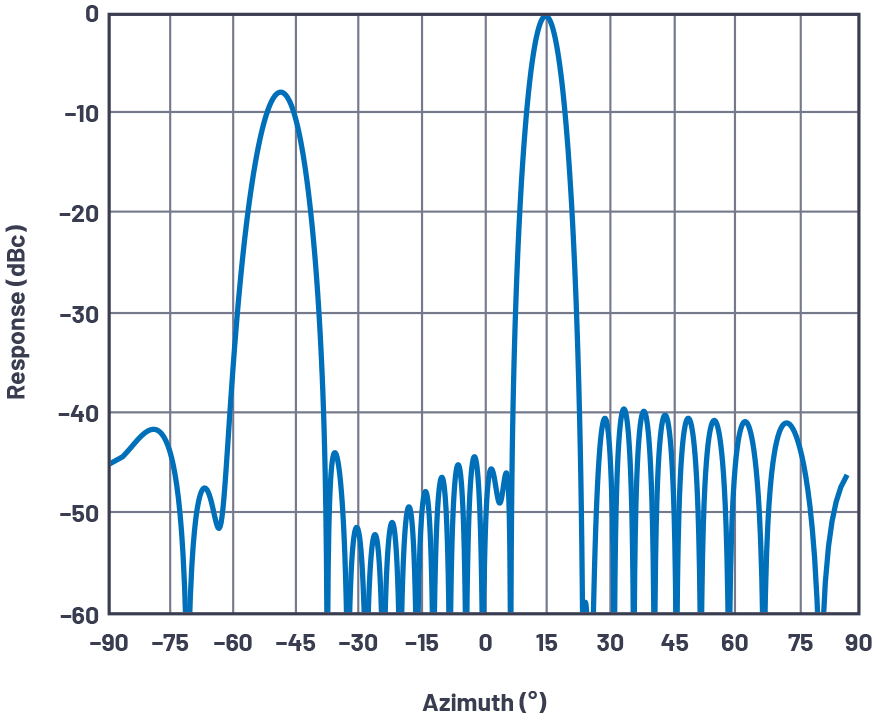
图9.最坏情况下的天线量化旁瓣：2位，n = 1，30个元件。

在光束角度除量化误差顺序为0和LSB/2的特殊情况外，均方根误差在孔径上分布时会减小。实际上，对于n偶数值的角度方程（公式3），量化误差为零。如果我们绘制各种移相器分辨率下最高量化旁瓣的相对电平，就会出现一些有趣的模式。图9显示了100元线性阵列的最坏情况QSLL，它采用汉明锥度，以便量化旁瓣与本节前面讨论的经典窗口旁瓣区分开来。

请注意，在 30° 时，所有量化误差都归零，这可以证明是 sin（30°） = 0.5 的结果。请注意，任何特定n位移相器的最坏情况电平的光束角在任何更高分辨率n下都表现出零量化误差。可以看到此处描述的最坏情况下旁瓣电平的波束角，以及每比特分辨率QSLL的6 dB改进。

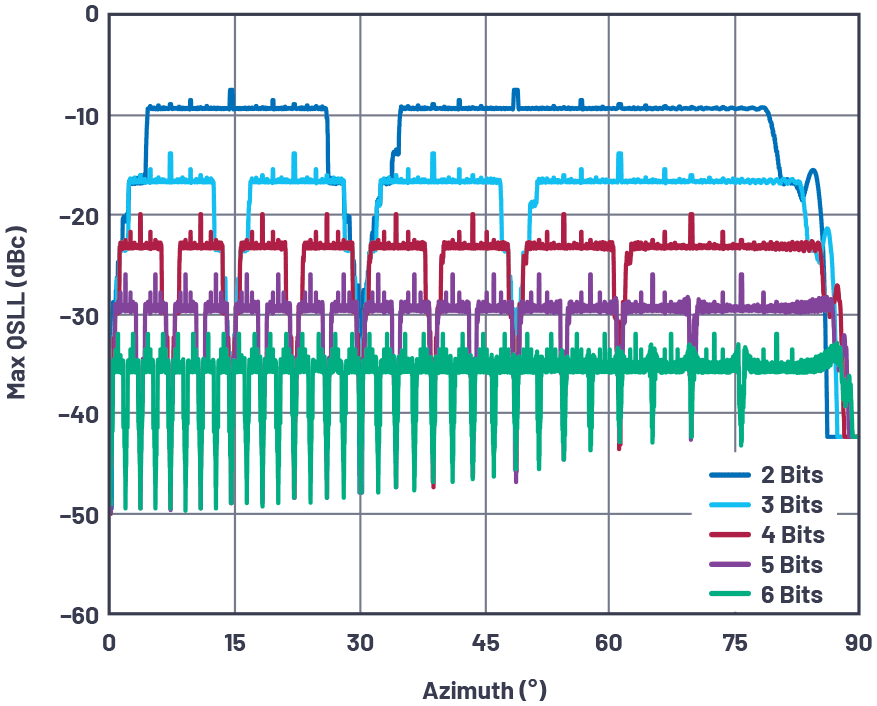
图 10.移相器分辨率为2位至6位的最差情况量化旁瓣与波束角的关系。

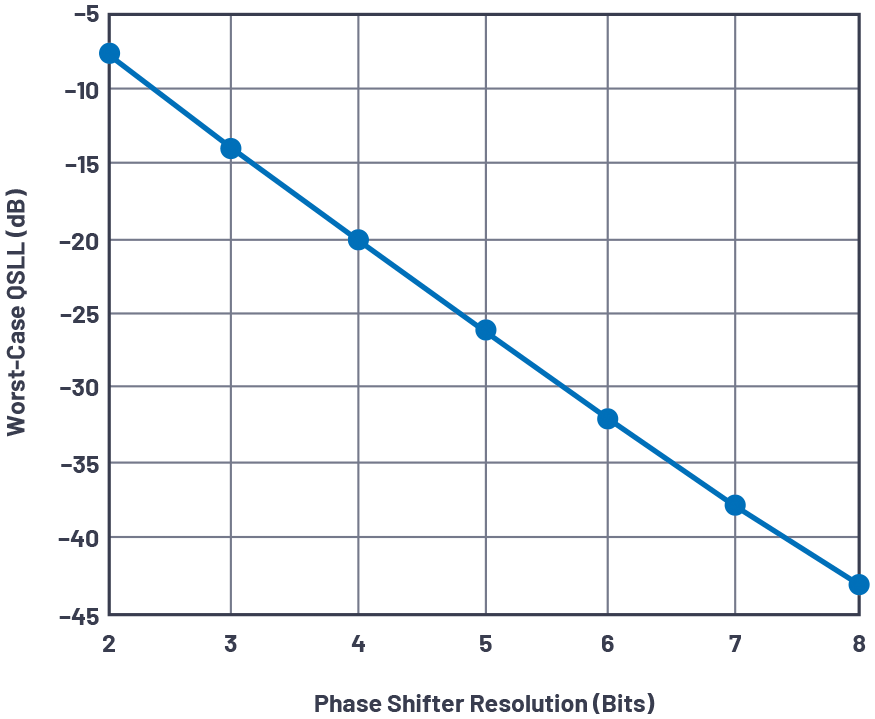
图 11.最差情况量化旁瓣电平与移相器分辨率的关系。

2位至8位移相器分辨率的最大量化旁瓣电平QSLL如图11所示，该电平遵循数据转换器熟悉的量化噪声定律。

或每比特分辨率约 6 dB。在2位时，QSLL电平约为–7.5 dB，高于对随机信号进行采样的数据转换器的经典+12 dB。这种差异可以看作是在整个孔径上对周期性发生的锯齿误差进行采样的结果，其中空间谐波在相位中增加。请注意，QSLL不是孔径大小的函数。

结语

现在，我们可以总结一下天线工程师相对于波束宽度和旁瓣面临的一些挑战：

角分辨率需要窄光束。窄光束需要大孔径，这需要许多元件。此外，当转向远离视线时，光束会变宽，因此随着扫描角度的增加，需要额外的元件来保持光束宽度。

似乎可以在不添加额外元件的情况下增加元件间距以增加整体天线面积。这会缩小光束，但不幸的是，如果元件间距均匀，则会引入光栅瓣。可以探索减小扫描角度以及实现有意随机化元件模式的非周期性阵列，以利用增加的天线面积，同时最大限度地减少光栅瓣问题。

旁瓣是另一个问题，我们了解到可以通过将阵列的增益逐渐减小到边缘来缓解。然而，锥形是以加宽光束为代价的，同样需要更多的元素。移相器分辨率可能会引入量化旁瓣，天线设计中也必须考虑到这一点。对于使用移相器实现的天线，波束斜视现象会导致角偏移与频率的关系，从而限制了高角分辨率的可用带宽。

关于相控阵天线方向图的三部分系列文章到此结束。在第 1 部分中，我们介绍了波束指向、阵列因数和天线增益。在第 2 部分中，我们介绍了光栅瓣和光束斜视的缺陷。在第 3 部分中，我们讨论了逐渐减小和量化误差。其目的不是针对精通电磁和辐射元件设计的天线设计工程师，而是针对从事相控阵工作的相邻学科的大量工程师，他们可能会从对影响整体天线方向图性能的各种影响的直观解释中受益。

审核编辑：郭婷