

OpenCV入门之OpenCV的基本操作4
电子说
描述
8、算子操作: sobel 算子、 scharr****算子、拉普拉斯算子、Canny边缘检测
Sobel算子是一种离散的微分算子 ,结合高斯平滑和微分求导运算。该算子利用局部差分寻找边缘(近似等于微分),计算所得的是一个梯度的近似值,用来边缘检测的。
Sobel算子对图像求一阶导数,一阶导数越大,说明像素在该反向变换越大,边缘信号越强。Sobel算子采用离散差分算子计算图像像素点亮度值的近似梯度。

综合考虑两个方向的变化:

scharr算子与sobel算子类似
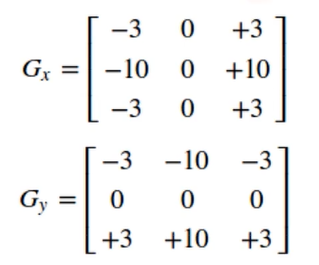
Laplacian算子则是求二阶导
注:

一般情况下:
(1)一阶导数通常会产生较粗的边缘;
(2)二阶导数对精细细节,如细线、孤立点和噪声有较强的响应;
(3)二阶导数在灰度斜坡和灰度台阶过渡处会产生双边沿响应;
(4)二阶导数的符号可以确定边缘的过渡是从亮到暗还是从暗到亮;
(5)二阶导数对细节更敏感。
def EdgeDetection():
# ---识别图像的边缘---#
# 边缘是像素值发生跃迁的位置,
# sobel算子,[[-1,0,1],[-2,0,2],[-1,0,1]]
# 对图像求一阶导,一阶导数越大,说明像素在该方向变化越大,边缘信号越强
chess = cv2.imread('./images/qi.jpg')
dx = cv2.Sobel(chess,-1,1,0,ksize=3)
dy = cv2.Sobel(chess,-1,0,1,3)
img_sobel = cv2.add(dx,dy)
img_sobel1 = cv2.addWeighted(dx,0.5,dy,0.5,0)
# scharr算子[[-3,0,3],[10,0,10],[-3,0,3]]
dx = cv2.Scharr(chess,-1,1,0)
dy = cv2.Scharr(chess,-1,0,1)
img_scharr = cv2.add(dx,dy)
# 拉普拉斯算子,二阶求导
img_Lap = cv2.Laplacian(chess,-1,ksize=3)
# 卷积实现
kernel = np.array([[0,1,0],[1,-4,1],[0,1,0]])
img_L = cv2.filter2D(chess,-1,kernel)
# canny边缘检测
# 一般步骤:
# 1、先进行去噪,高斯滤波
# 2、求梯度,对平滑后的图像用sobel算子求梯度和方向,
# 方向用arctan(Gy/Gx),方向被归为4类,垂直水平和两个对角线
# 3、非极大抑制:去除不是边界的点,遍历图像,判断当前点是否是周围像素点中具有相同方向上的梯度最大值
# 4、滞后阈值,设定边界,最小和最大,保留之间的,且是连续的
img_canny = cv2.Canny(img,30,50)
cv2.imshow("imshow", np.hstack((img_Lap,img_L)))
cv2.waitKey(0)
cv2.destroyAllWindows()
Canny边缘检测算法
1、高斯模糊——gaussian
2、灰度转换——cvtColor
3、计算梯度——Sobel/Scharr
4、非最大信号抑制
5、高低阈值输出二值图像
第一步:使用高斯滤波器进行滤波,去除噪音点
第二步:使用sobel算子,计算出每个点的梯度大小和梯度方向
Sobel核在水平和垂直方向上对平滑的图像进行滤波,以在水平方向(Gx)和垂直方向(Gy)上获得一阶导数
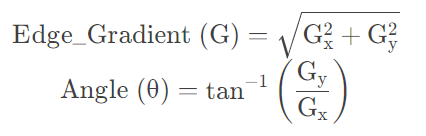
第三步:使用非极大值抑制(只有最大的保留),消除边缘检测带来的杂散效应
在获得梯度大小和方向后,将对图像进行全面扫描,以去除可能不构成边缘的所有不需要的像素。为此,在每个像素处,检查像素是否是其在梯度方向上附近的局部最大值。
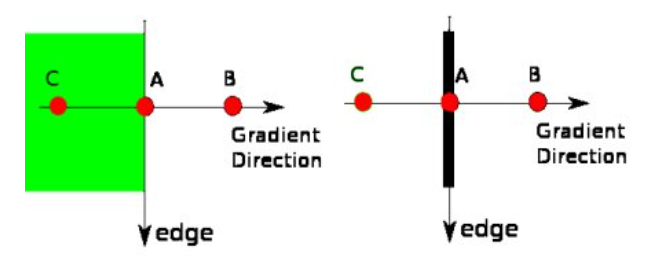
点A在边缘(垂直方向)上。渐变方向垂直于边缘。点B和C在梯度方向上。因此,将A点与B点和C点进行检查,看是否形成局部最大值。如果是这样,则考虑将其用于下一阶段,否则将其抑制(置为零)。简而言之,得到的结果是带有“细边”的二进制图像。
第四步:应用双阈值(磁滞阈值),来确定真实和潜在的边缘
需要两个阈值minVal和maxVal。强度梯度大于maxVal的任何边缘必定是边缘,而小于minVal的那些边缘必定是非边缘,因此将其丢弃。介于这两个阈值之间的对象根据其连通性被分类为边缘或非边缘。如果将它们连接到“边缘”像素,则将它们视为边缘的一部分。否则,它们也将被丢弃。
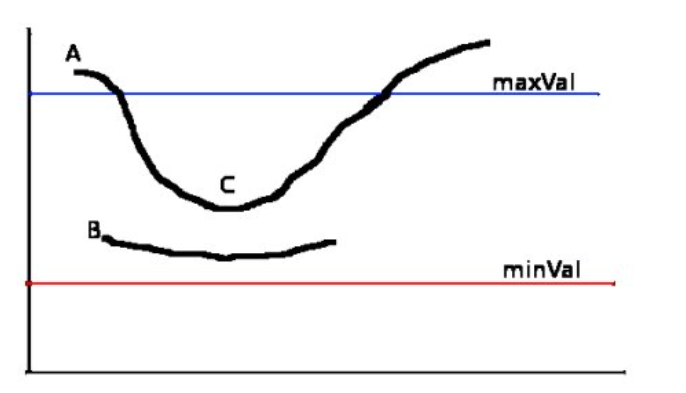
边缘A在maxVal之上,因此被视为“确定边缘”。尽管边C低于maxVal,但它连接到边A,因此也被视为有效边,我们得到了完整的曲线。但是边缘B尽管在minVal之上并且与边缘C处于同一区域,但是它没有连接到任何“确保边缘”,因此被丢弃。因此,非常重要的一点是我们必须相应地选择minVal和maxVal以获得正确的结果。
-
OpenCV入门之OpenCV的基本操作12023-02-07 1249
-
用OpenCV进行基本绘图_《OpenCV3编程入门》书本配套源2022-05-11 476
-
OpenCV3编程入门-源码例程全集-OpenCV开发环境的配置2016-09-18 586
-
基本鼠标操作_《OpenCV3编程入门》书本配套源代码2016-06-06 522
-
OpenCV_编程简介(入门必读)2016-03-21 746
全部0条评论

快来发表一下你的评论吧 !

