曲面加工优化方法有哪些？

改编自：《新一代智能化数控系统》（作者：陈吉红，杨建中，周会成）

在数控加工中，有很多提高曲面加工质量的手段，如高速高精运动控制、误差补偿和振动抑制。本文主要介绍轨迹平滑和速度优化对曲面加工质量的提升和优化。

**「 **1．曲面加工轨迹平滑方法 」

---

CAM系统生成的刀具路径通常是G0连续（仅位置连续）的分段线性路径。程序段之间G1不连续（切向不连续），会导致数控系频繁降速，影响加工效率。插补轨迹G2不连续意味着曲率不连续，此时如果降速不充分，会引起较大的加速度波动，造成机床的剧烈振动，影响加工质量。因此，为了保证加工效率和加工质量，Gk（k>=2）连续的刀具路径平滑是高性能数控系统的重要性能之一。

在数控加工中，刀具轨迹拟合方法主要分为插值和逼近两种。当刀具轨迹顺序通过给定的刀位点时，这种刀具轨迹称为插值轨迹；当拟合的轨迹不严格通过刀位点，只是在设定的误差范围内接近给定的刀位点，我们称这种刀具轨迹为逼近轨迹。目前，在轨迹拟合方面的研究主要分为以下几类。

1）局部样条构造轨迹

局部样条构造方法是通过在每两个刀位点之间构造一段样条，并保证样条的弓高误差来控制样条拟合的精度。这种拟合方法具有局部性好，计算简单，算法实时性好，适用于数控系统的实时数据处理流程。局部样条构造方法认为刀位点反应了原始模型的特征，构造的样条严格通过每一个刀位点，避免造成零件特性信息丢失影响零件加工精度，如图1所示。

图1 刀位点之间的局部样条构造

样条构造的一种方式是以相邻两个点的坐标及点的切向量为边界条件，在两个点之间构造一段样条。点的坐标值不变，切向量方向可以通过各个点前后点的坐标插值得到，切向量的模长可以利用相邻的小线段长度进行估算，如图2所示。通过该方法构造出来的样条能够严格控制其形状和对小线段的逼近精度，具有较好的局部特性，但样条间通常只达到了G1连续。

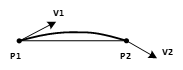
图2 两点之间构造样条

另外，这种样条构造的方式对点的切向量估算要求比较高，如果切向量估算不准，容易造成样条变形。为了提高边界条件的准确性，有文章中提出在CAM生成刀具轨迹时，利用模型信息将刀位点处的切向量和误差指向信息同时输出到文件中，指导数控系统完成更加精确的样条构造。其中弦误差指向信息是两点（P0、P6）之间弦高差最大的位置和方向CHORD_ERR[w,e,l]，如图3中的P3点处，w为小线段上弦高差最大位置的比例，e表示最大的弦高差，l表示弦高差的方向。

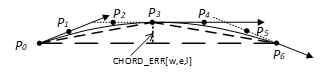
图3 包含切向和误差指向信息的样条构造

这种样条构造的方式可能得到更高的精度和更合适的轨迹形状，但是对CAM的信息要求较高，目前还不具有通用性。

构造样条的另一种方式是以小线段为单位，在两个小线段之间插入过渡样条，并保证过渡样条与两侧直线段的连续性。如下图中的B3(u)和B4(u)两段样条即为构造的过渡样条，这两段样条可以通过6个控制点（Q1～Q6）进行描述。

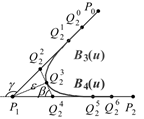
图4 小线段之间的过渡样条构造

然而，有文章认为，这类样条过渡的方式虽然保证了样条的G2连续，但过渡样条没有通过编程刀位点，可能造成零件特性信息的丢失并引起相邻轨迹的横向不均匀。为了解决不通过编程刀位点的问题，该文章提出先构造G2甚至G3连续的过渡样条，再通过迭代的方式对过渡样条进行变换，使其在很小的误差范围内通过编程刀位点，如图5所示。

图5 通过编程刀位点的局部过渡样条

以上局部构造的方法虽然最大程度地通过编程刀位点，但是没有考虑小线段轨迹中的噪点（缺陷点），对G代码要求较高，实际工程应用中难以普及。另外，这类方法由于是在两个刀位点或两段小线段之间插入局部样条的方式构造整个刀具轨迹，缺乏全局轨迹拟合的光顺特性。

2）插值样条拟合轨迹

另一些研究人员是通过离散编程点计算每个程序段转角处所对应的“离散曲率”，并判断连续小线段轨迹的偏转情况，将偏转超过阈值的转折点作为可光顺区域的边界特征点。然后利用B样条曲线对边界特征点之间的点进行插值拟合，以达到整体光顺的目的，如图6所示。

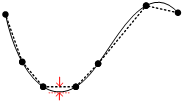
图6 刀位点的全局插值拟合

该方法避免了两个特征点之间点的切向不连续问题，轨迹压缩率较高，可有效提高编程点之间轨迹运行时的进给速度。但是该类方法对光顺后的轨迹与原始轨迹之间的误差并没有做严格的限制，很难保证插值后的加工精度。

为了提高这类插值轨迹的拟合精度，有文章提出选择性的插值拟合，先将能够拟合为样条的小线段轨迹进行分组，例如每5个点一组，采用三次Bezier曲线对一组刀位点的第一个刀位点P1、第三个刀位点P3和最后一个刀位点P5进行插值，然后判断P2、P4点相对于样条的误差是否满足逼近精度，如果满足则直接输出样条；如果不满足则对P3处的参数进行调整或插入更多的点，直到满足中间点的逼近精度，如图7、图8所示。

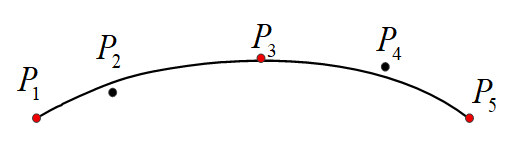
图7 三次Bezier曲线插值P1、P3、P5示意图

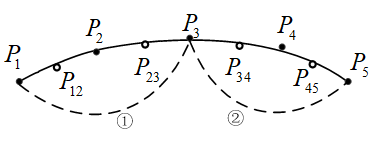
图8 增加刀位点重新分组示意图

在得到一系列Bezier曲线后，利用B样条的性质，将多条三次Bezier曲线转换为一整条三次B样条，形成最终的插值轨迹，这种选择性地刀位点插值轨迹能够降低多点拟合的计算复杂度，并能有效提高插值精度。

3）逼近样条拟合轨迹

还有一些研究和实际应用是利用样条曲线对离散编程点进行逼近拟合（图9）。为保证拟合曲线的逼近精度，需要对拟合后的曲线与原始刀位点之间的误差进行检查，并通过迭代与分段拟合的方法进一步提高对原有刀位点的逼近程度。这类方法保证了对刀位点的拟合精度，在提高轨迹的全局光顺性的同时实现了数据的压缩，但是其误差校验过程中需要计算点到曲线的距离，并可能需要多次迭代，算法耗时较高且具有一定的不确定性，因此这类算法对系统的硬件处理速度和软件流程具有很高的要求。

图9 刀位点的全局逼近拟合

在逼近样条拟合轨迹方面多个知名的数控系统厂商也具有较多的研究和应用。

德国SIMENS的高档数控系统840D、840D sl及最新的SINUMERIK ONE中均集成了小线段程序压缩器和可编程角度倒圆功能（图10）。程序压缩器能够根据所设的公差带将行程指令按顺序压缩成一条平滑的、曲率稳定的样条轮廓，有利于提高系统速度和加速度，从而提高生产率。可编程角度倒圆是通过预读，对已知尖锐转角进行圆弧倒角，即不严格通过编程角点。

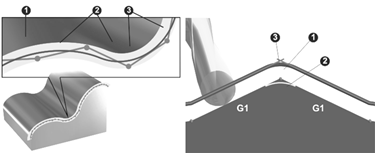
图10 SIMENS的程序段压缩和可编程转角过渡功能

日本FANUC的30i、31i、32i等高档数控系统推出了智能平滑公差控制功能（图11）。与SIMENS类似，智能平滑公差控制功能一方面可以根据指定允差平滑连续微小线段指令的加工路径，提高精加工的质量；另一方面通过指定公差，可实现不同指令间的转角过渡，包括直线与直线、直线与圆弧、圆弧与圆弧插补的平滑过渡。

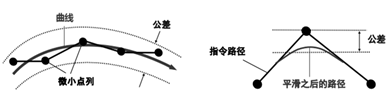
a平滑连续小线段 b允差内转角过渡

图11 FANUC的智能平滑公差控制功能

同样，海德汉（HEIDENHAIN）高档数控系统TNC620、TNC640等也具有类似的功能，如自动控制平滑处理。这些产品化的高端轨迹平滑技术使得以上企业的产品在高性能数控系统领域中占据了绝对的优势，但其技术实现目前处于保密状态，一般的专业人员难以深入了解其技术细节。

从以上轨迹平滑的理论研究和实际应用中可以看出。局部构造样条轨迹和插值拟合轨迹虽然能够保证严格通过特征刀位点，最大程度忠实于CAM软件生成的编程轨迹，但是对于存在缺陷点的编程轨迹适用性较差，容易发生轨迹变形和异常降速。全局逼近轨迹能够过滤编程轨迹中的异常波动，甚至对噪点也能够起到平滑的作用，曲线光顺性较好，对于加工速度的提升具有较大意义，但是全局逼近拟合方法需要计算刀位点与逼近曲线的距离，并需要进行多次迭代才能够提高轨迹的拟合精度，算法耗时较高，对系统软件硬件性能要求较高，工程应用中的技巧性较强。

然而，从SIMENS、FANUC和HEIDENHAIN所公布的轨迹平滑功能原理简介中可以看出，其所用的方法均是全局逼近拟合配合局部转角过渡的方式进行刀具轨迹的平滑处理，因此可以看出该方法对曲面加工优化具有较高的适用性。

**「 **2．曲面加工速度优化方法 」

---

在曲面加工中，通常速度越高，加工误差越大。通过降低加工速度来提升精度会影响零件的加工效率。另外，速度的不平稳、加速度突变可能会导致加工表面出现振纹。速度的横向不连续会引起加工表面刀纹不均匀。因此，在数控系统插补前需要对加工速度进行合理地优化。速度优化需要考虑两个方面：一方面是确定单条轨迹上各程序段的合理速度，另一方面是保证相邻轨迹的速度连续性。其中，如何保证相邻轨迹的速度连续性是速度优化的难点。

目前，在相邻轨迹连续性速度优化方面的研究主要分为两类：一类是在数控系统前瞻阶段，通过跨相邻轨迹的大范围程序段预读，在确定单条轨迹速度的同时考虑相邻轨迹的速度连续性；另一类是在离线环境下，通过对全局轨迹的遍历和迭代，实现相邻轨迹间的速度连续。

1）系统前瞻速度优化

前瞻是数控系统相对于当前加工的程序段，超前预读和处理还未加工到的程序段，并将处理后的待加工程序段放入系统缓存中，等待系统的加工。前瞻是保证系统正常运行、提高加工效率和加工精度的关键。在前瞻的过程中需要识别降速区域和拐角尖点，并确定降速区域和拐角尖点处的最大加工速度，保证刀具平稳地通过所有刀位点。根据前瞻范围的不同又可以划分为两类：一类是短距离的预读，仅识别轨迹行进方向的降速区间和拐角尖点，并计算降速速度；另一类是在大范围程序段预读的基础上，不仅对轨迹行进方向的降速区间和拐角尖点进行识别，还能够建立多条相邻轨迹的空间邻近关系，实现加工速度的横向连续，避免个别轨迹缺陷点导致的异常降速。

有研究认为，降速区间的分界点通常是刀具轨迹中曲率不连续和切向不连续的特征点，如图12所示。在前瞻中识别出降速区间和拐角尖点后，再对其降速的速度值进行合理地限定，以保证曲面加工精度和效率。在一个降速区间内，加工速度在边界处快速变化到指定的速度并保证恒定，直到下一个降速区间或拐角尖点的出现。恒定的速度有助于提高加工过程的稳定性，因此这类速度优化方法在一定程度上能够改善加工表面质量的均匀性。

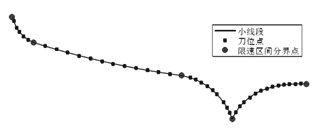
图12 降速区间分界点和拐角尖点

然而这类方法也只考虑了行进方向的降速区间和拐角尖点，没有考虑相邻轨迹的降速区间和降速尖点的一致性。为了解决这个问题，需要在大范围前瞻基础上，利用相邻轨迹匹配的算法对降速区间和降速尖点进行一致性规划。如图13所示，当刀具加工到当前点时，系统最远前瞻程序段已经跨越了多条轨迹，通过对前瞻轨迹中的刀位点邻近关系和轨迹形状进行匹配，使相邻轨迹的降速区间边界点和拐角尖点的位置协调一致，并且保证预规划速度大小的横向连续。图中前瞻范围内的相邻4条轨迹的速度标记点V1、V2、V3和V4的位置和大小基本保持一致。

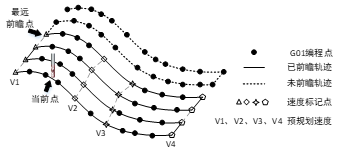
图13 考虑相邻轨迹的前瞻速度预规划

西门子、海德汉和FANUC等系统厂家在这方面具有较深入地研究和应用，在系统性能允许范围内，尽可能多地预读程序段，然后通过刀位点的邻近关系和轨迹的形状匹配，实现相邻几条轨迹的降速区间和拐角尖点的速度协调。

西门子840D及以上版本的高端数控系统推出了连续路径运行功能和优化后的前瞻预读功能。连续路径运行功能通过修改局部编程曲线，在轨迹达到平滑后，使得程序段过渡时轨迹速度不会降到很低，尽可能以稳定的速度运行连续的小线段程序。优化后的前瞻预读功能通过对相邻铣削轨迹中相似的轨迹特征进行预处理，使相邻铣削轨迹上的速度保持协调，对任意形状表面上的往复加工质量均有良好的效果。

海德汉TNC640高档数控系统的高级动态预测（ADP）功能同样对预读能力进行了扩充。在双向往复铣削路径中，使进给速度在往复平行路径中达到“对称”，并对速度曲线进行特定的平滑。即使对相邻路径刀位点分布不均匀的NC程序，也能缩短加工时间，提高表面光洁度。

FANUC 31i及以上版本高端数控系统的AI轮廓控制功能通过预读程序指令来提前判断轨迹形状，自动区分拐角及曲线的特征，并根据机床的机械性能对速度及加速度进行优化，以提高加工效率。该功能强调了系统预读能力，在预读时完成轨迹平滑和速度优化任务，其部分系统型号最大预读程序段达到1000段。

2）离线全局速度优化

在系统前瞻时进行速度优化，能够在加工的同时进行优化处理，效率较高。然而，受系统实时性的限制，前瞻范围虽有所增加但仍然有限，只能考虑相邻几条轨迹速度的一致性，无法保证全局轨迹速度的横向连续。

离线全局速度优化是在系统外部的优化软件中，在不受实时性和内存的限制下，利用复杂度更高的全局遍历和迭代优化算法，实现加工轨迹的全局速度优化。离线全局速度优化的结果可以通过文件输入到数控系统，数控系统按照文件中的速度优化结果进行加工，能够有效避免由于数控程序缺陷和系统实时性限制导致的加工表面缺陷，提高加工质量和加工效率。如图14所示，离线全局速度优化标记出的降速区间边界（白色点），在轨迹横向上形成连续的“特征线”，特征线上所有标记点的速度大小保证一致性或连续性。

图14 离线全局速度区间优化

研究发现，数控系统的实时数据在插补点曲面上分布的不连续程度与曲面精加工表面质量缺陷之间存在对应关系。

在以上研究的基础上，通过采集数控系统加工过程中的实时插补数据，利用插补点压缩算法和曲面重构算法对各信号（如速度、加速度等）在曲面上分布情况进行可视化，利用实时数据的不连续度量化算法对信号的不连续度进行评价，作为曲面加工全局速度优化的参考依据。

在实时插补数据分析的基础上，有文章提出通过定位每个刀位点在相邻轨迹上的投影位置，重构刀位轨迹的横向信息，利用横向信息查找特征点的候选点，然后筛选候选点以形成特征线，计算特征线划分的速度区间的边界速度，并利用平滑算法对横向速度区间的目标速度进行一致性优化。

离线优化的方式虽然能够完全地实现全局速度优化，但是由于需要在系统外部进行额外的预处理，操作流程相对复杂，优化结果在不同系统中无法直接复用，因此主要用于对全局表面质量要求较高、单件零件价值较高的复杂零件。