

16位定点数字信号处理编程是怎么思考的
描述
前言:如果说要在16bit定点环境上使用DSP算法,如IIR构成的2P2Z,会受到定点编程和量化精度的问题。如果说在float32环境上可以很容易进行编程,那切换到定点环境上就不得不得考虑这些问题。通常情况下单精度浮点在小数点后的精度为1/(2^23),理论上使用32位定点IQ24就可以覆盖单精度浮点的精度问题,但是在16bit上,使用i1.q15的方法来算,仅有1/(2^15)的精度,如果直接使用则会遇到量化精度引起的误差问题。那么该如何把浮点切换到16bit的定点来呢,下面将一步一步的来进行讨论。
S1 传递函数离散
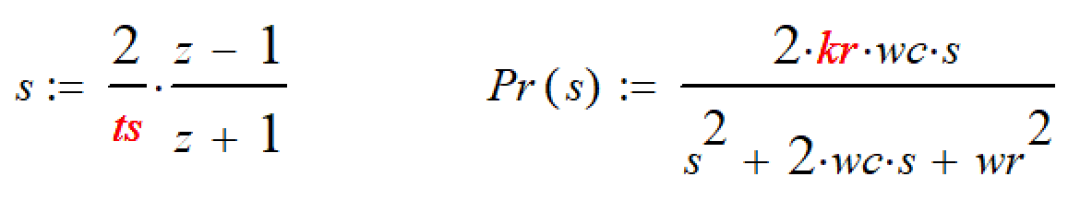
离散化:
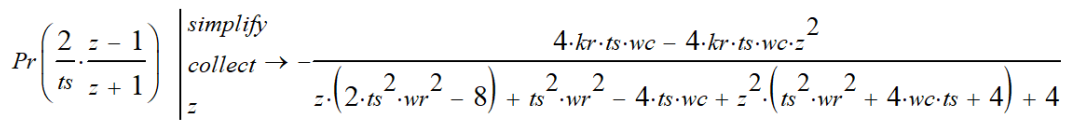
带入参数,并出归一化的z域传递函数,这里把分母的z^2提出来,然后全部除以其它的数字,即可得到:
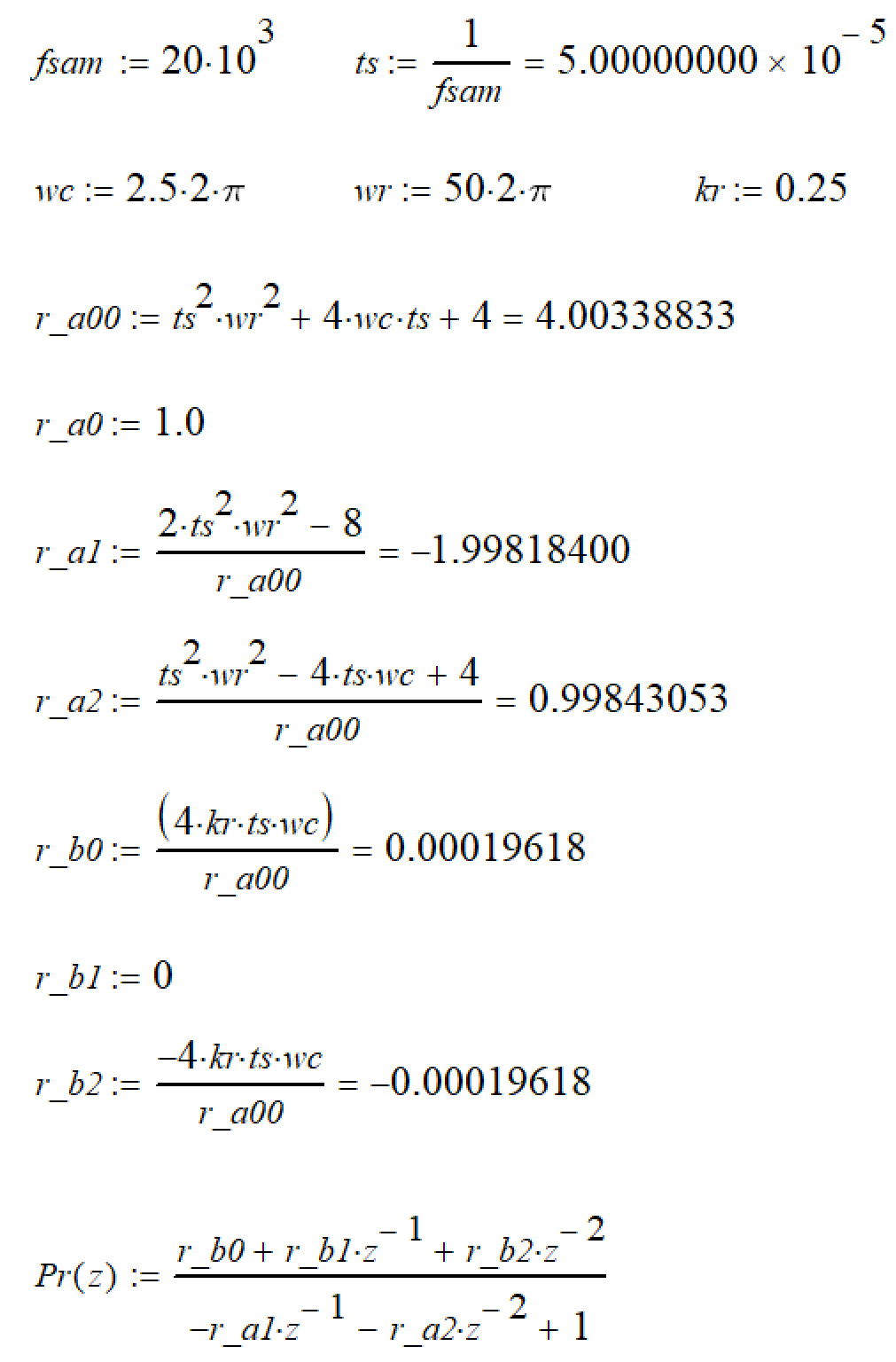
S2 使用IQ15的方法量化:
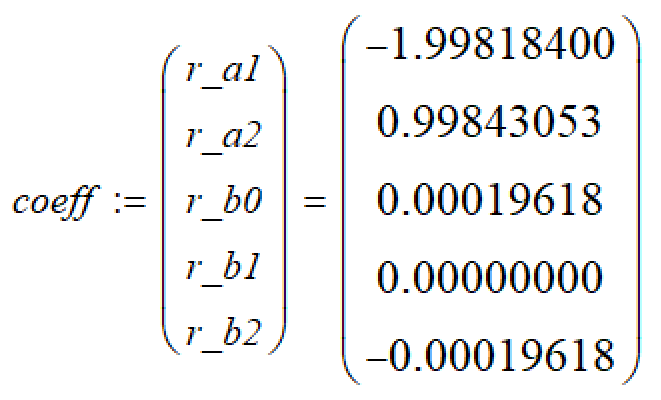
可见,a1项为最大,即可把全部数字除以a1项,让它用满15bit的字长,可得:

然后乘以2^15,得到:
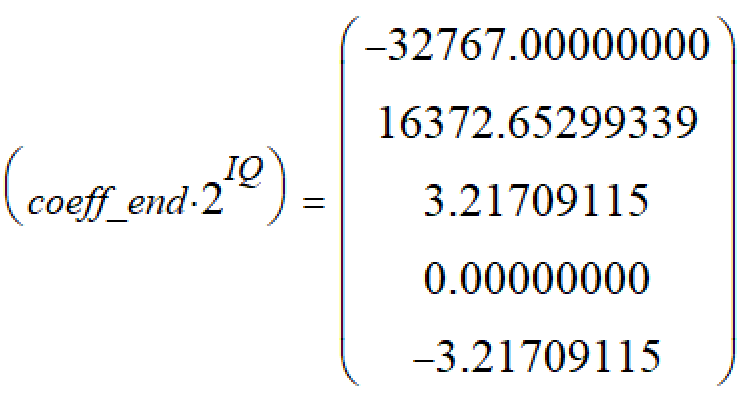
S3 提升B系数:这里可以看到分子项上B0/B2的数字太小,所以为了提高量化精度,可以在B系数上继续扩大到2^12,这样可以更多的利用字长,最后在输出上除去引入增益即可。
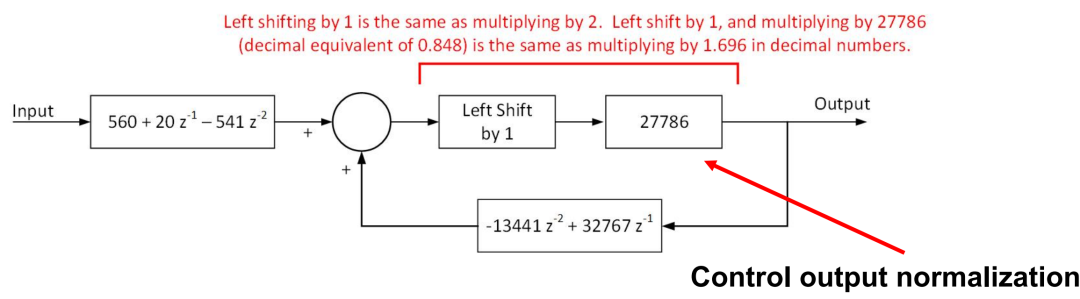
可得B系数更新为。
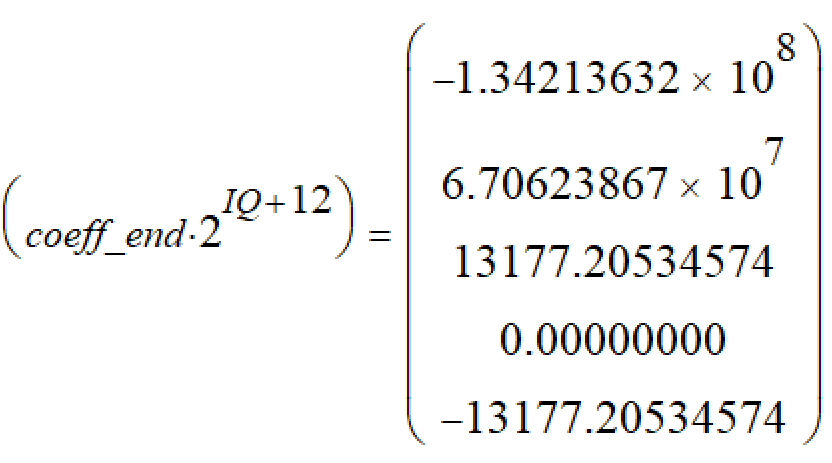
然后考虑一下分母量化为32786时引入的增益:1.99998,在编程上考虑先左移1位然后再考虑小数点(32709/32678)即可引入增益。然后开始测试定点化后的PR控制器:

S4 测试:输入测试信号为50hz正弦波:
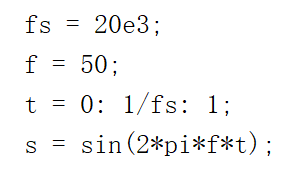
run,这里使用floor函数,进行向下取整来进行定点化:

S5 输出:可见定点和浮点的输出波形几乎接近,存在很小的误差,属于可以接受的量化精度。
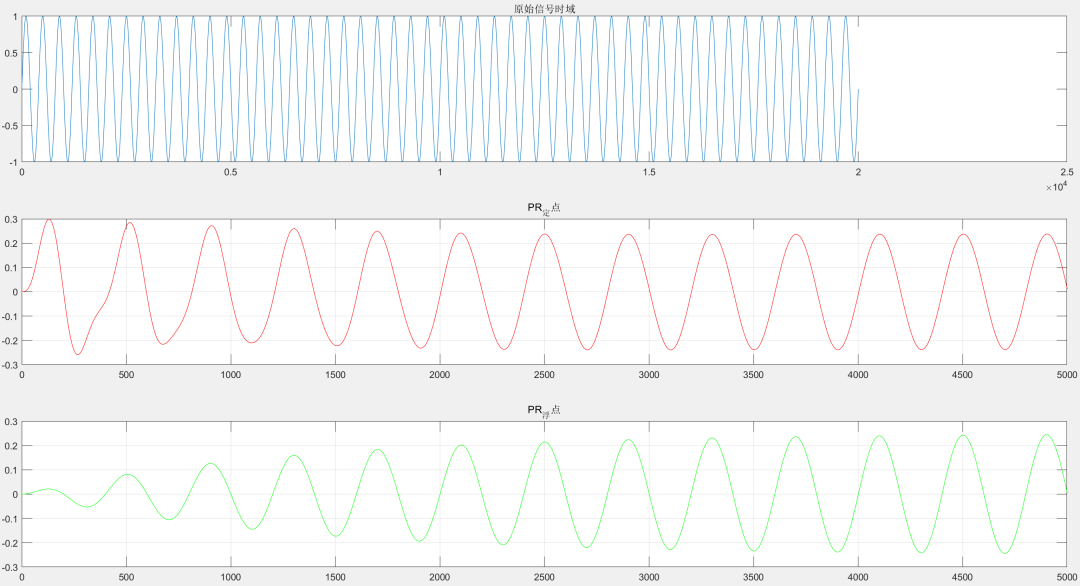
小结:可见在充分利用上32768的精度后,PR控制器很好的运行在16bit环境上,如果是32bit的定点环境,则无需这么麻烦,直接使用I6Q24即可达到单精度浮点的精度。本人能力有限,如果错误恳请帮忙指正,谢谢观看。
-
SM320C6424-EP定点数字信号处理器数据表2024-08-08 322
-
TMS320C5517定点数字信号处理器数据表2024-08-07 449
-
TMS320VC5416定点数字信号处理器数据表2024-08-05 411
-
TMS320C6421定点数字信号处理器数据表2024-08-03 365
-
SMJ320C6203定点数字信号处理器数据表2024-08-02 325
-
TMS320VC5505定点数字信号处理器资料的英文详细概述2018-04-26 924
-
定点数字信号处理器(DSP)技术与应用2010-04-07 687
全部0条评论

快来发表一下你的评论吧 !

