离散化与代码实现

前言：
 

  一直有在用比例谐振控制器，是在matlab里面用C2D函数离散好了后直接使用参数，对于不同的电网频率还需要修改一下参数。而且在运行过程中发现网侧频率改变也不能实时修改PR的控制参数来达到最佳的控制效果，因此我需要能在MCU里面实时进行PR多个系数的计算，提取，更新的操作。

 

 

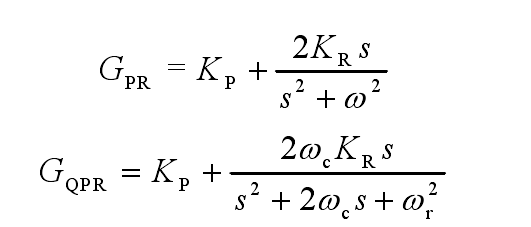
  QPR因为缓解PR在谐振点的增益以及有更好的适应性，而被广泛使用。传递函数中的wc用来调节QPR控制器在谐振点的增益带宽，wc越小则QPR在谐振的增益峰值越接近PR。kr是QPR控制器在谐振点的增益值，wr则是QPR控制器的设定谐振频率。参考文献1中展示了一张不同的kr和wc的QPR的bode图，可见：
 

 

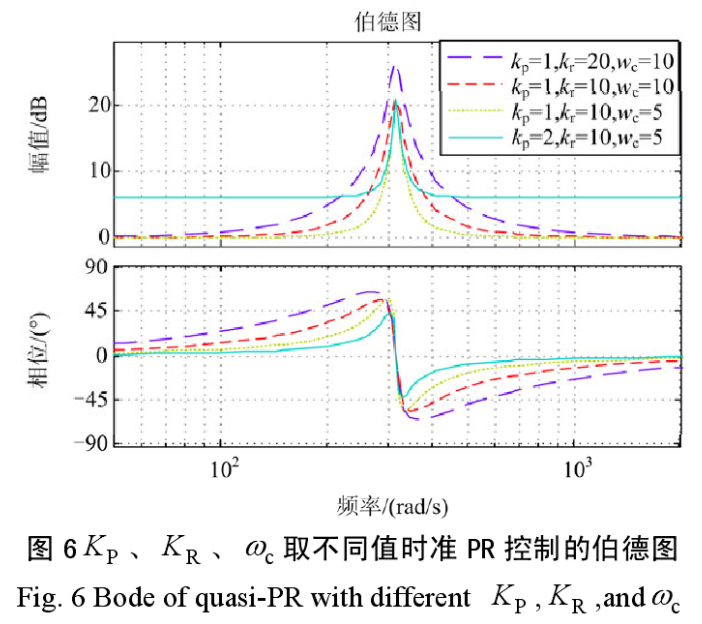
   所以我们要在MCU中运行这个传递函数，第一步是需要将其进行Z变换离散化后得到Z域传递函数的系数，第二步是运行这个传递函数。

 

我们先来看第一步：使用双线性变换来得到Z域传递函数。根据双线性变换的公式，可以计算到这个QPR的s域传递函数到Z域的传递函数。

 

 

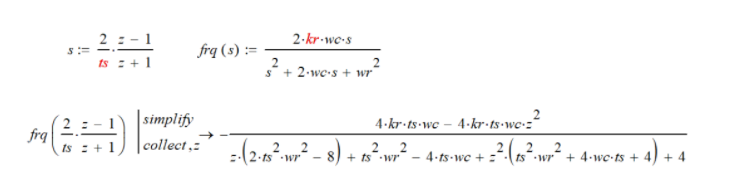
  从上图来看，是一个典型的二阶Z域传递函数，但是有点麻烦的地方是分母的Z^2的系数不是1，因此还需要对其进行改写一下，我把分子和分母都同时除以分母Z^2项的系数，从而使得这个传递函数可以提取标准化系数：B0,B1,B2,A1,A2，可见：
 

 

ts_x_ts = ts * ts;

wr_x_wr = wr * wr;

div_x = ts * ts * wr * wr + 4.0 * wc * ts + 4.0;

 

coeff_B0 = (4.0 * kr * wc * ts)/div_x;

coeff_B1 = 0;

coeff_B2 = -1*coeff_B0;

 

coeff_A1 = (2.0 * ts_x_ts * wr_x_wr - 8.0)/div_x;

coeff_A2 = (ts_x_ts * wr_x_wr - 4.0 * ts * wc + 4)/div_x;

 

  经过上面的处理后，即可得到标准的2阶Z域传递函数的系数，可见Matlab的输出：
 

pr_1st_z = c2d(pr_1st, ts, 'tustin')  %Matlab自带函数

pr_1st_Z = tf([coeff_B0 coeff_B1 coeff_B2], [1 coeff_A1 coeff_A2], ts)  %自己手动

 

两者输出一致，验证了正确性。
 

pr_1st_z =

 

  0.03912 z^2 - 0.03912

  ----------------------

  z^2 - 1.992 z + 0.9922

Sample time: 2.5e-05 seconds

Discrete-time transfer function.

 

pr_1st_Z =

 

  0.03912 z^2 - 0.03912

  ----------------------

  z^2 - 1.992 z + 0.9922 

Sample time: 2.5e-05 seconds

Discrete-time transfer function.

 

  第二步就是使用IIR滤波器来根据上面提取的系数来得到所需的输出了，其代码为：
 

        w(1) = inputl(i)  - w(2) * a_coff(2) -  w(3) * a_coff(3);

     yout(i) = (w(1) * b_coff(1) + w(2) * b_coff(2) +w(3) * b_coff(3)); 

        w(3) = w(2);

        w(2) = w(1);   

 

  第三步打包封装
 

   我们的目的是使用QPR对1，3，5，7，9，11次谐波进行抑制，如果各个传递函数的kr和wc一致，则只需要调整wr到各个频率即可。可以编写一个IIR二阶系统提取函数，根据所需的频率进行计算即可。  最后在把KP和低通滤波器引入，LPF能提供一个在高频的增益衰减功能，用于提升多个PR组合后的传递函数的稳定性。

 

可见闭环控制器的传递函数最终为：

lpf = (flpf*2*pi/(s + flpf*2*pi));

sys_pr = kp + lpf * (pr_1st + pr_3st + pr_5st + pr_7st + pr_9st + pr_11st);

 

运行测试：
 

 

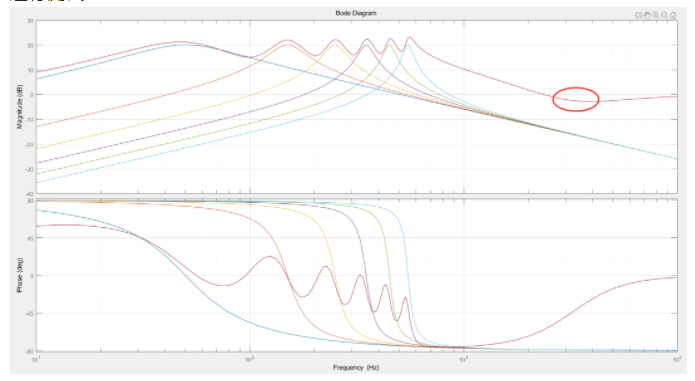
（3KHZ后 LPF开始起到作用）

 

编写QPR代码并运行测试，发现对3~5次谐波有抑制效果。
 

 

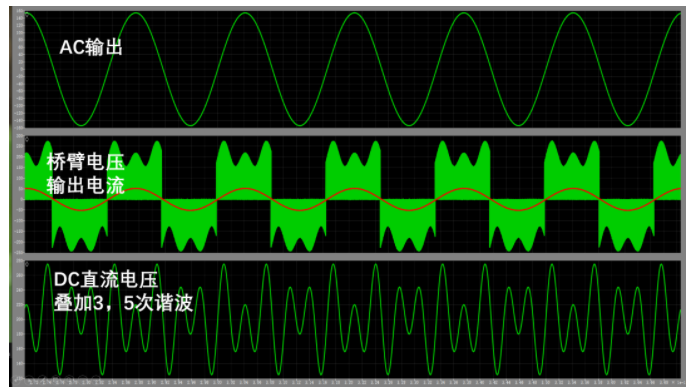
小结：根据s域传递函数计算出z域传递函数公式，并测试验证了准确性。
 

 

关于本人：

  我是杨帅，目前从事逆变器储能行业，专注在双向AC/DC变换器领域，对双向DC/DC的研究较多。数年来一直从事电力电子仿真技术研究与应用推广，致力于实现让天下没有难搞的电源而努力。