一文解析滤波器设计中的椭圆函数

引子

自打牛顿-莱布尼茨(Newton-Leibniz)发明微积分后, 整个数学和物理世界就不太平了, 早在1655年Wallis就开始研究了椭圆(ellipse)的弧长, 并且牛顿和Wallis都发表了关于椭圆弧长的级数表达式, 其次单摆周期的求解, 这些问题困扰了一代又一代人。

1679年雅各布·伯努利(Jacob Bernoulli)对弹性杆的研究中也遇到了椭圆积分, 并且得到了一个简单的椭圆积分的例子：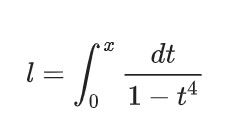

早期这个积分也叫双扭线积分(lemniscate integral), 并且伯努利也意识到了这个积分不简单, 并不能用初等函数表达。

1750年左右, 欧拉(Euler)发展了椭圆积分, 如椭圆积分的加法定理(Elliptic Integral Addition Theorems)和兰登变换, 以加法定理为例说明：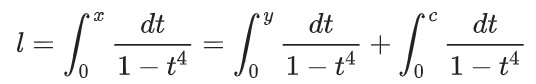

其中积分上限满足：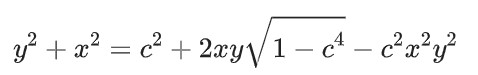

并且欧拉给出了其几何意义。

1785年拉格朗日(Lagrange)就发表了一篇关于椭圆积分的文章, 其中用到了AGM(Arithmetic-Geometric Mean, 算术几何平均数), 接着高斯独立的发现了AGM, AGM让椭圆积分的数值计算变得容易。

接着到了1826年勒让德(Legendre)开始全面论述了椭圆积分并著作《椭圆函数论》, 将椭圆积分归为三大类, 现称为椭圆积分的勒让德形式(elliptic integral in Legendre's form)：

本章节主要讨论和椭圆函数滤波器相关的第一类椭圆积分：

第一类不完全椭圆积分(incomplete elliptic integral of the first kind)：三角形式:

到了(1829年)雅可比(Carl.Gustav.Jacob.Jacobi)和阿贝尔(N.H. Abel)时代, 椭圆函数理论发生了质的变化, 这里最主要的贡献是椭圆积分反演, 也就是说我们不去直接研究椭圆积分, 而是研究椭圆积分的逆, 即原椭圆积分的积分上限为函数值, 积分值为自变量, 同时也发现了其逆的双周期性质。

对于第一类椭圆积分, 我们和定义正弦函数一样定义雅可比椭圆正弦函数满足如下等式：

为了解决函数的多值性所带来困扰, 黎曼把思考维度又提升一个层次, 将复平面拓展为许多叶的曲平面上, 思考维度从二维上升到了三维, 这时出现了黎曼曲面的概念了, 这里开辟了数学新战场--拓扑学。

当然, 以上是对椭圆积分的知识的一个简单渐进式的梳理。对于滤波器设计而言, 实际上我们关心第一类椭圆积分的一些性质和计算方法, 这里主要介绍双周期性和其数值计算方面。

若对椭圆积分和椭圆函数感兴趣的同学可以阅读扶教授的讲座笔记《椭圆积分和椭圆函数讲座回顾》。

理解雅可比函数的双周期性

数域的拓展

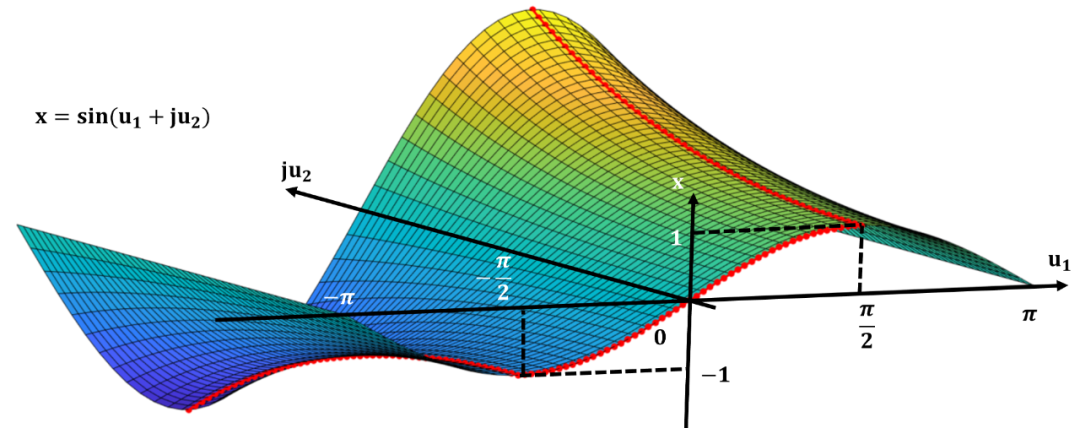
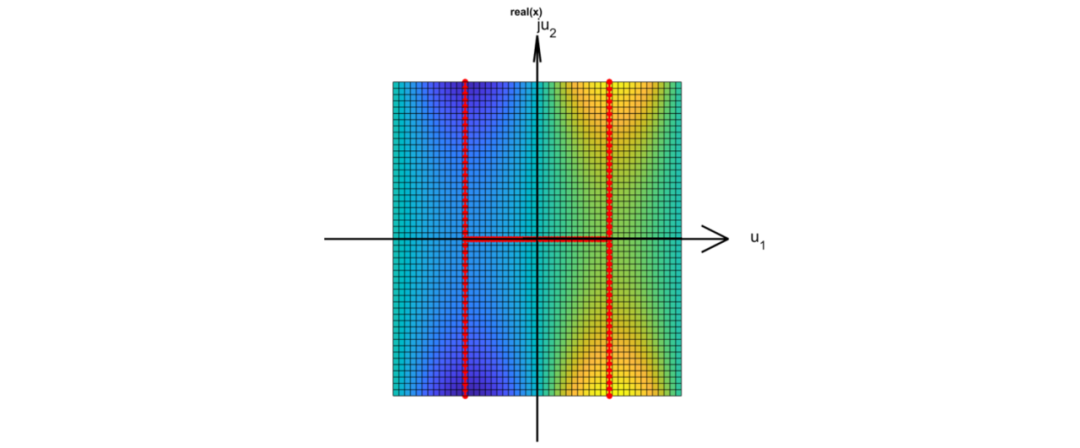
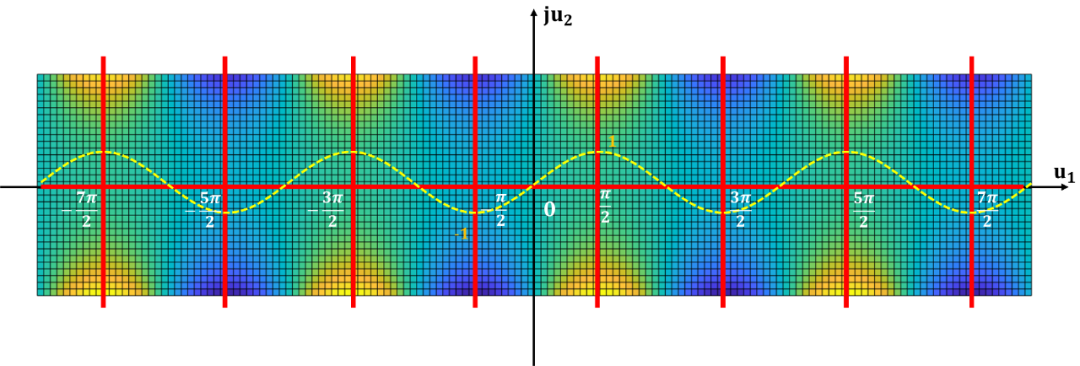
试想一下一个蚂蚁在这个复平面上爬, 那么如何爬, 其高度可以连续的从低到高?下图就展示了这一过程:

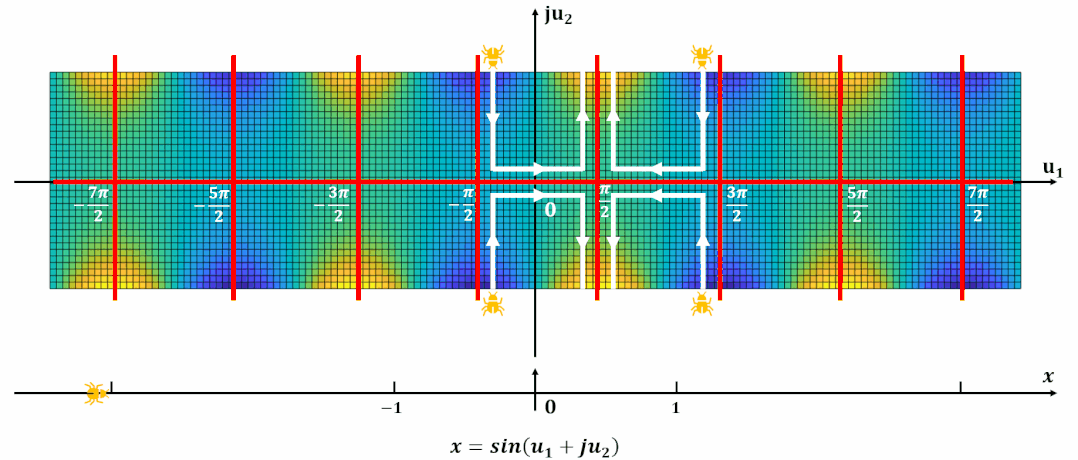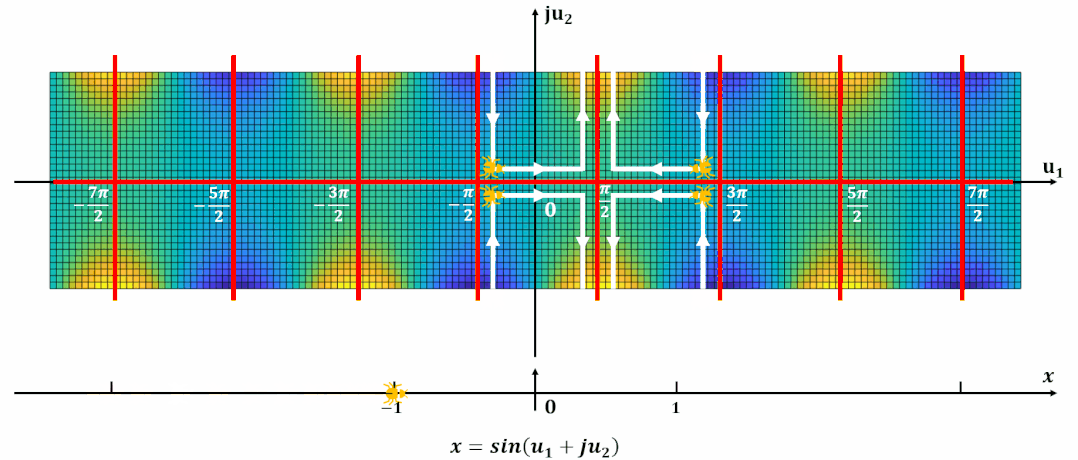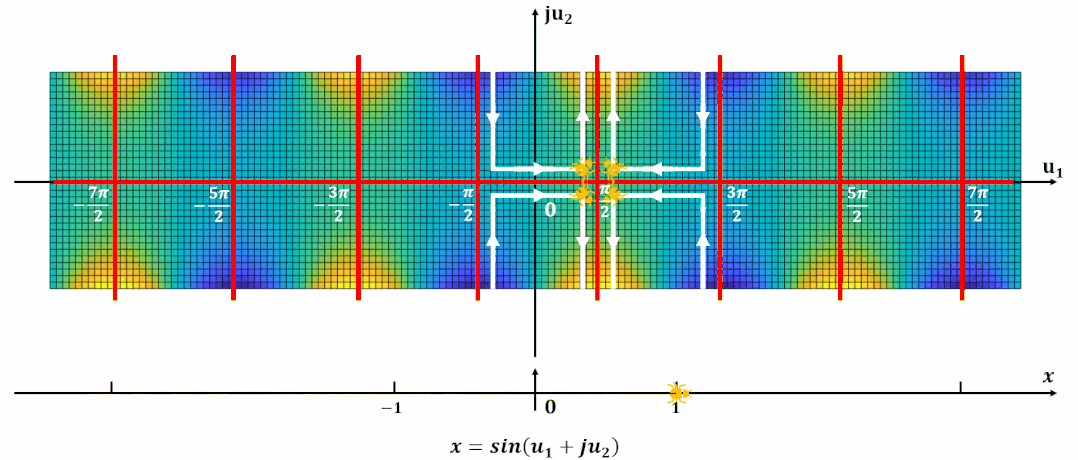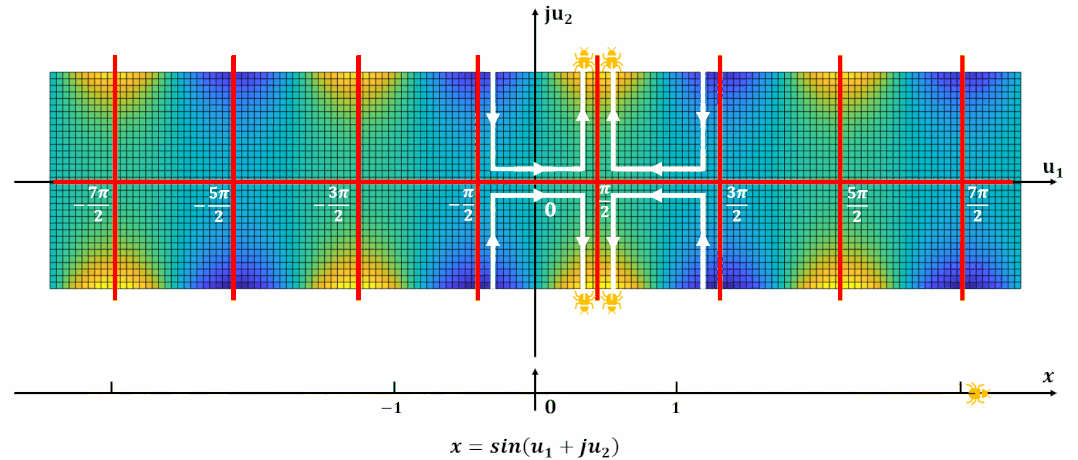
单周期

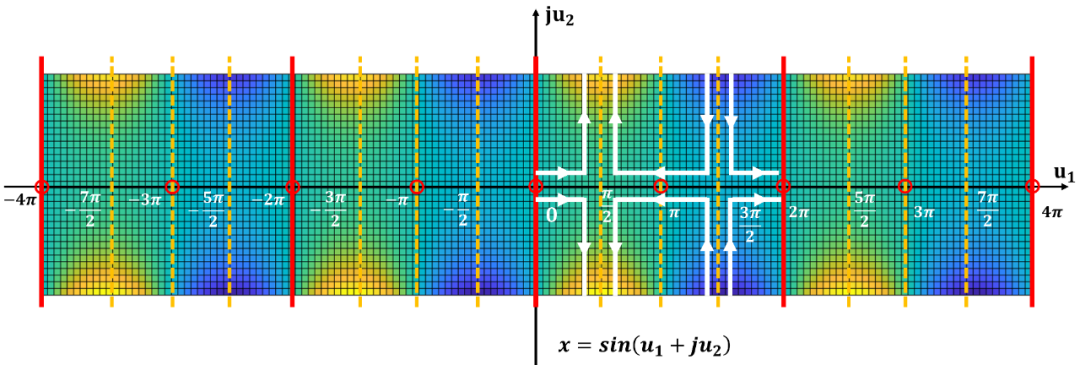
再简化一下, 得到：

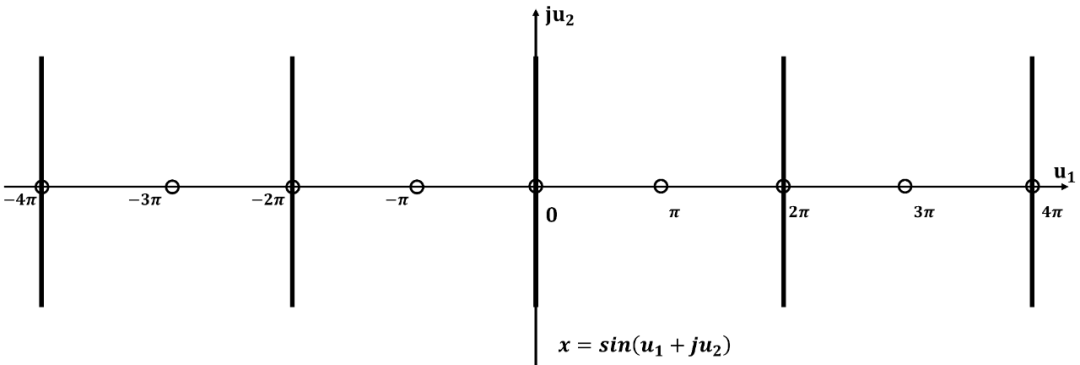
其周期带如下：

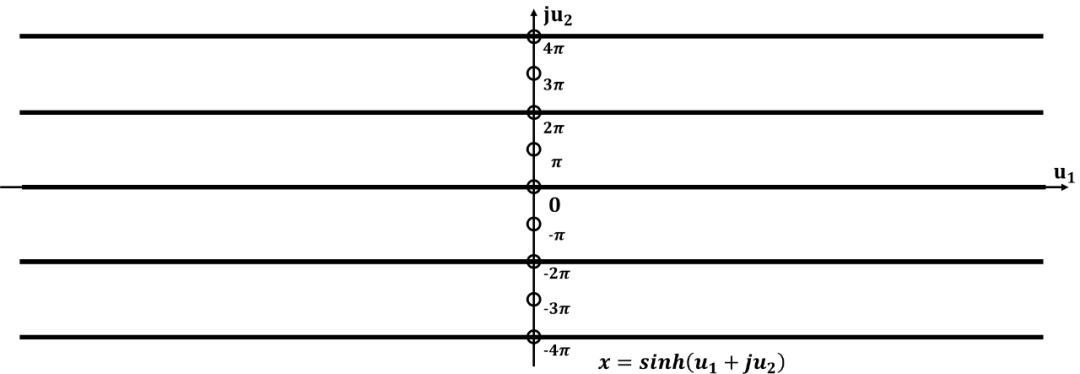
双周期

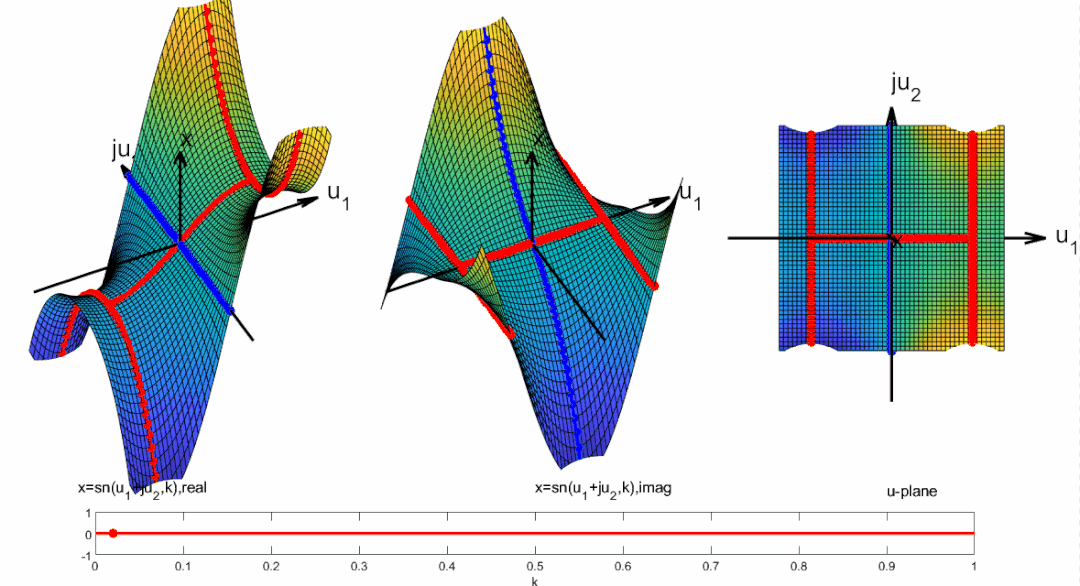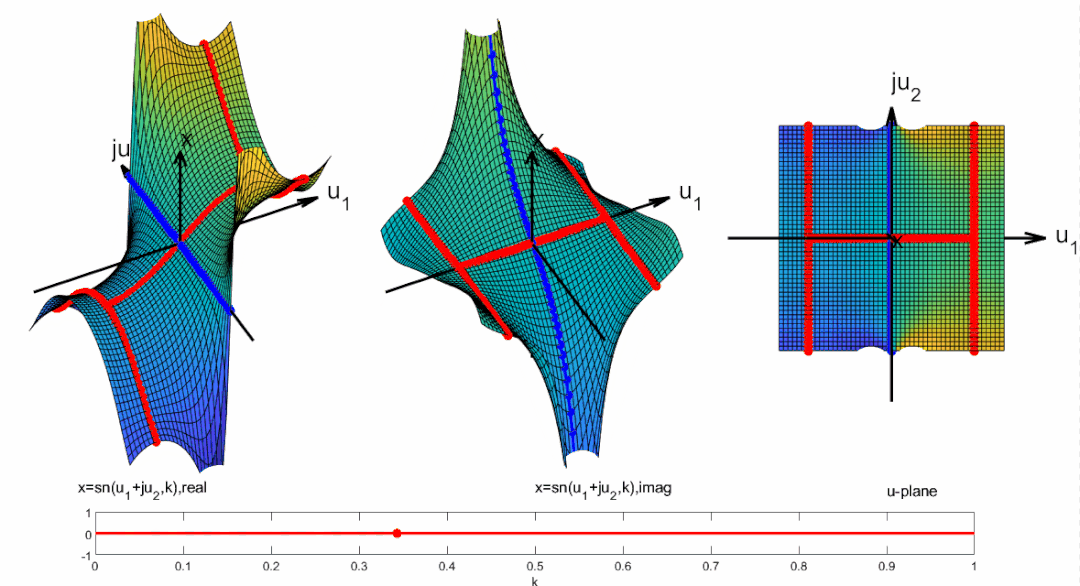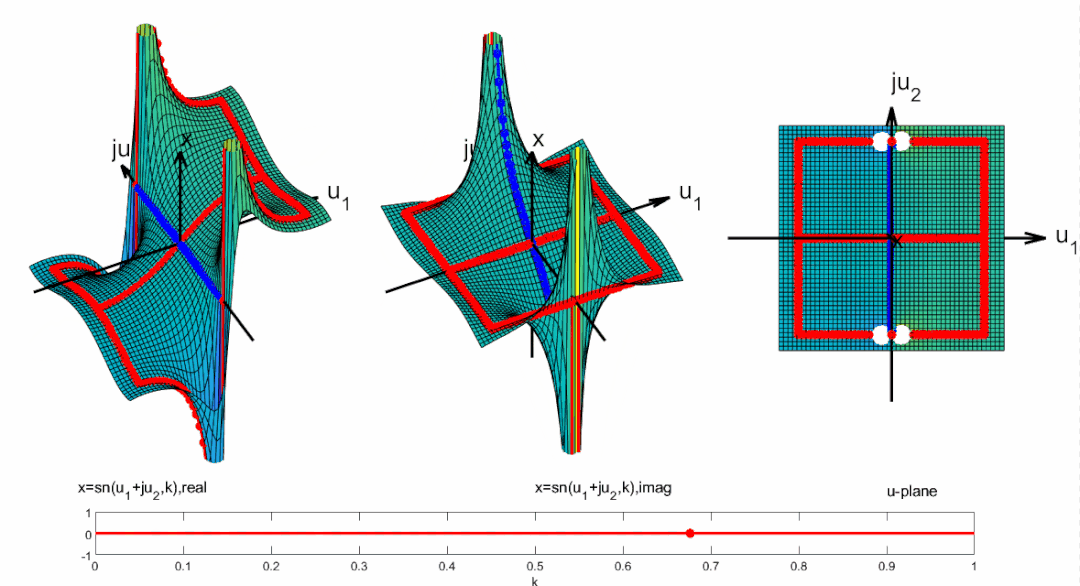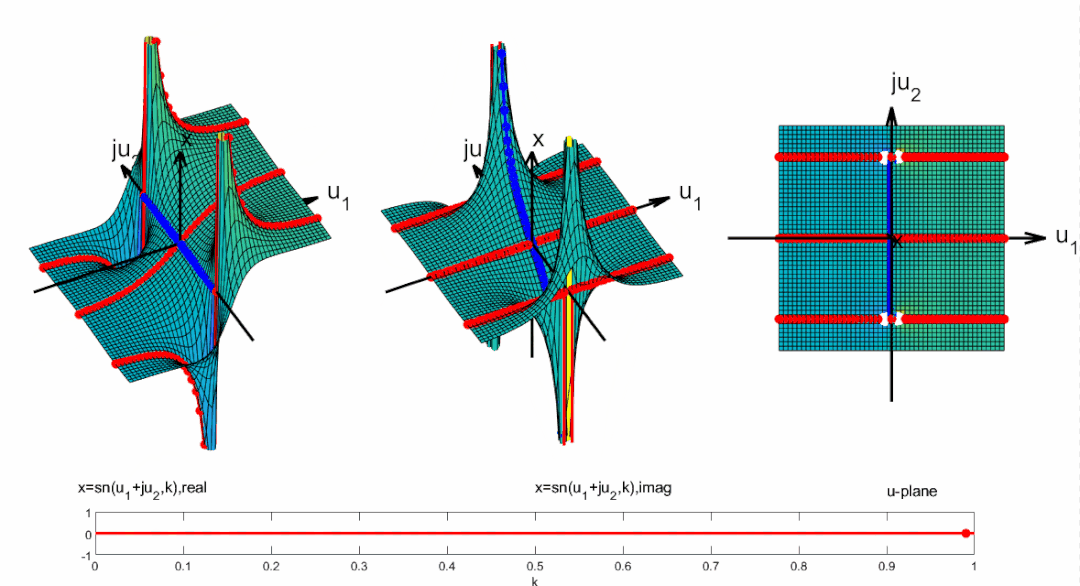
将周期向整个复平面拓展, 并且标出零极点位置:

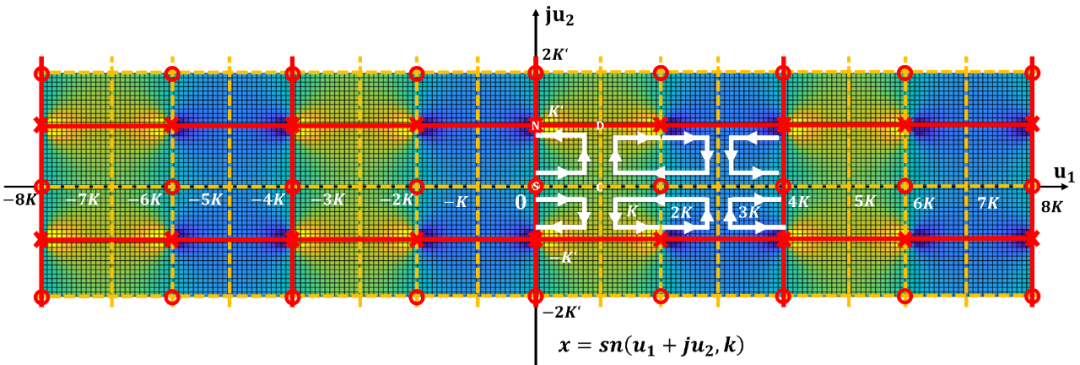
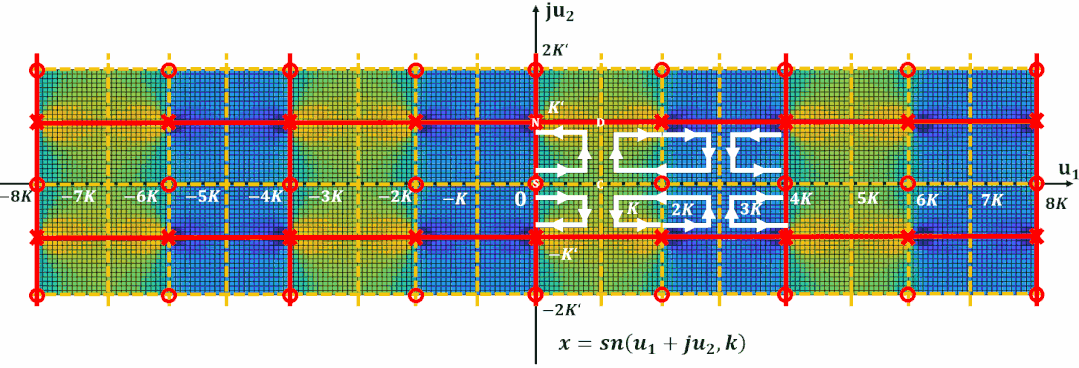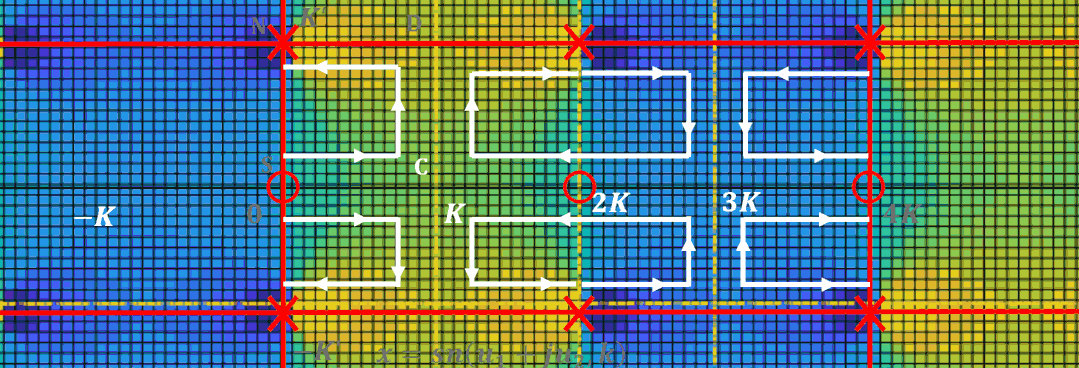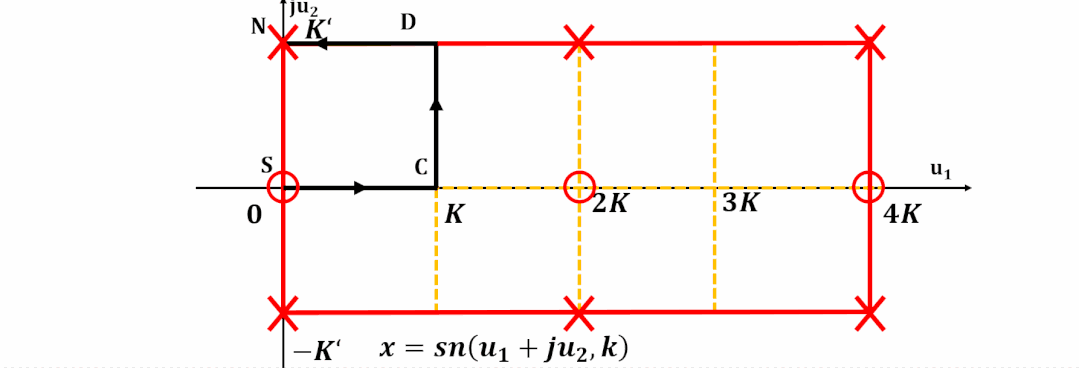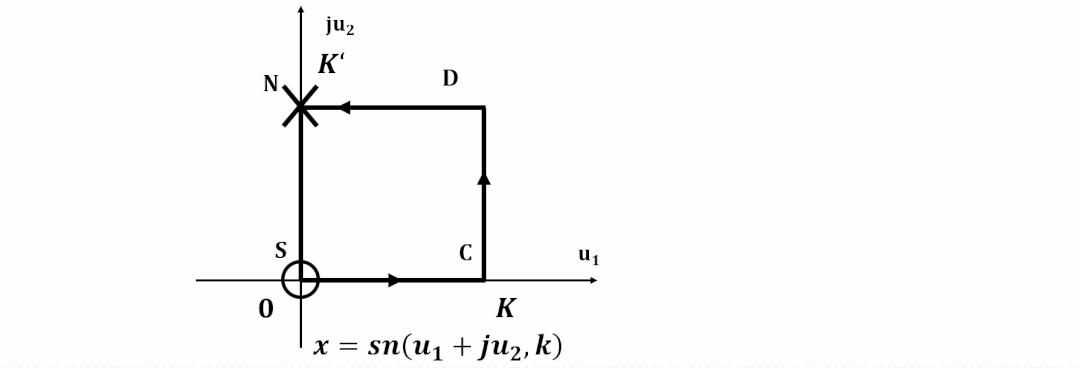
为了更容易对滤波器设计进行计算, 计算机程序都对雅可比椭圆函数进行了归一化。

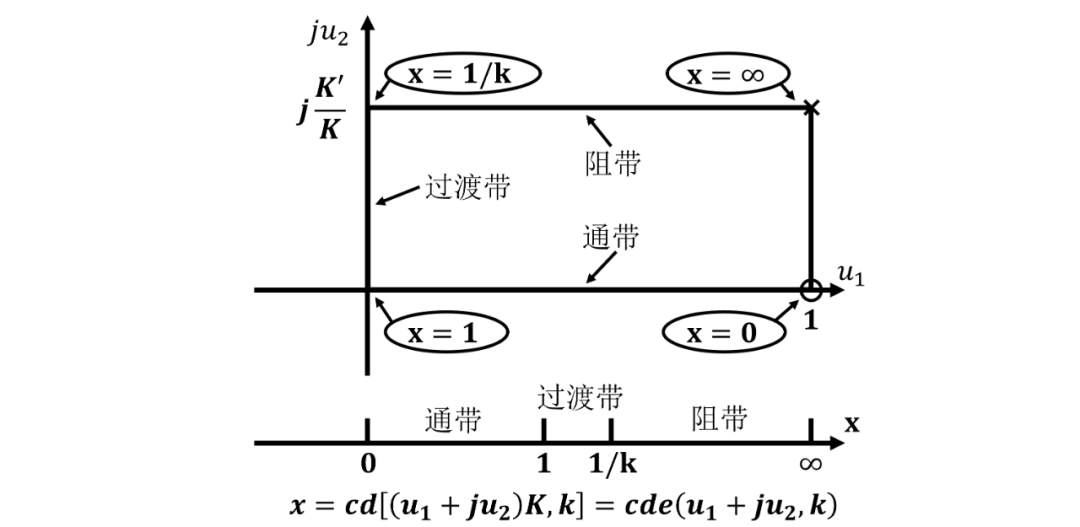
这样雅可比椭圆函数在-平面实轴上的周期为实数4, 更加方便分析和计算。

椭圆积分和雅可比椭圆函数的数值求解

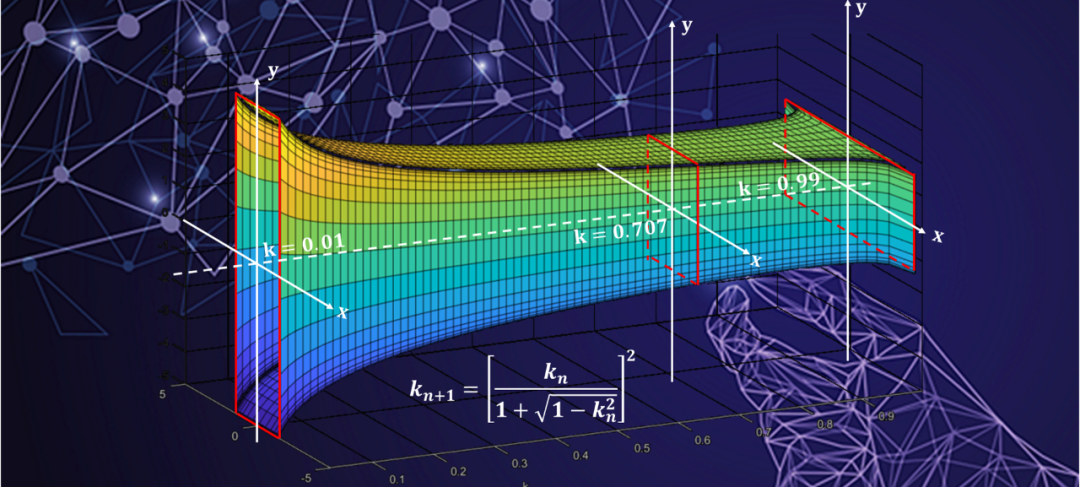
当然椭圆积分的数值计算方法有很多种, 除了兰登变换外, 还有数值积分和级数展开方法。

椭圆积分的数值计算

兰登变换(Landen Transformation)的几何解释如下:

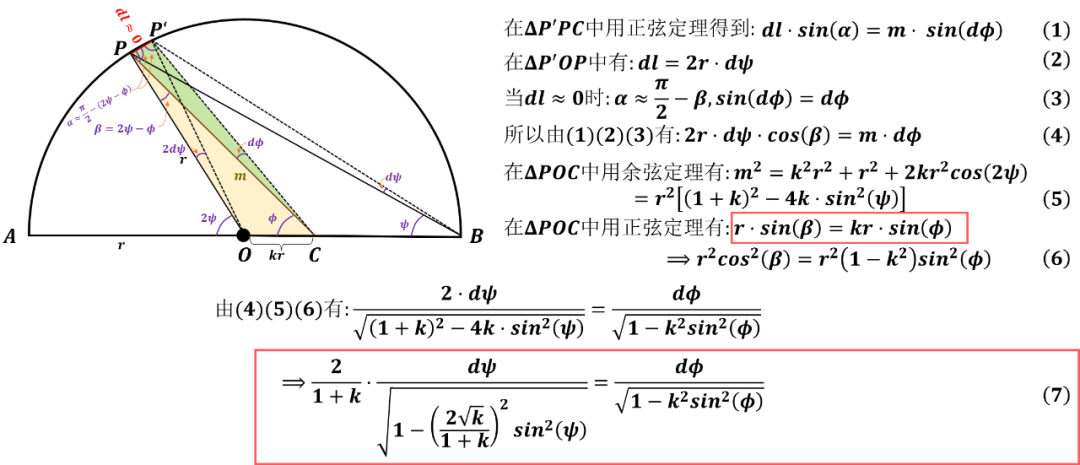
这样建立了椭圆积分的一般递推表达式。更多关于兰登变换的内容见《高斯，兰登，拉马努金，算术几何平均数，椭圆，  ，和女士日志》。

文献中提供了3种椭圆积分的数值求解方法:

方法1(模数递增)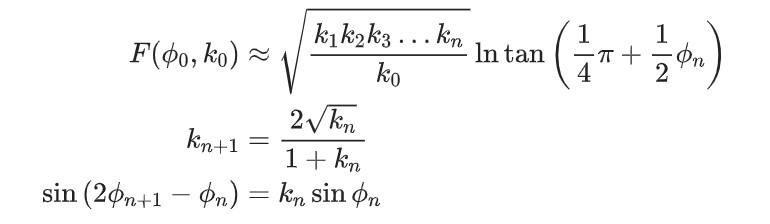

Matlab验证结果如下:

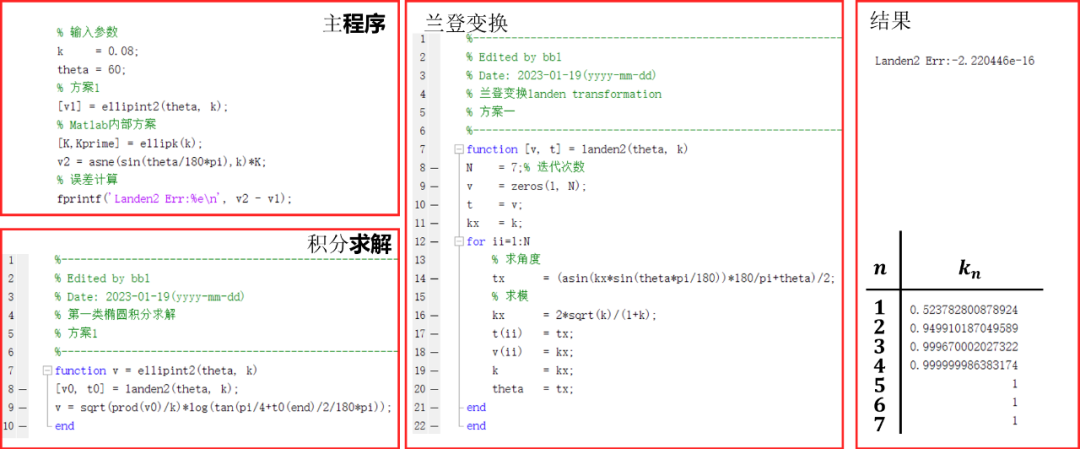
和Matlab原生态函数计算结果相差级别误差。

方法2(模数递减)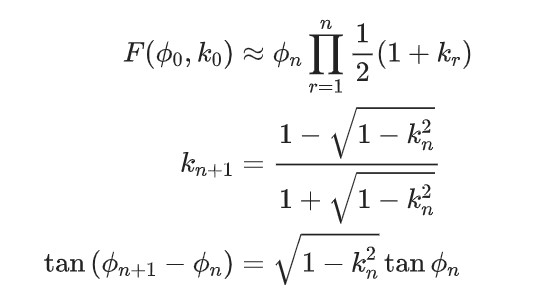

Matlab验证结果如下:

Matlab验证结果如下:

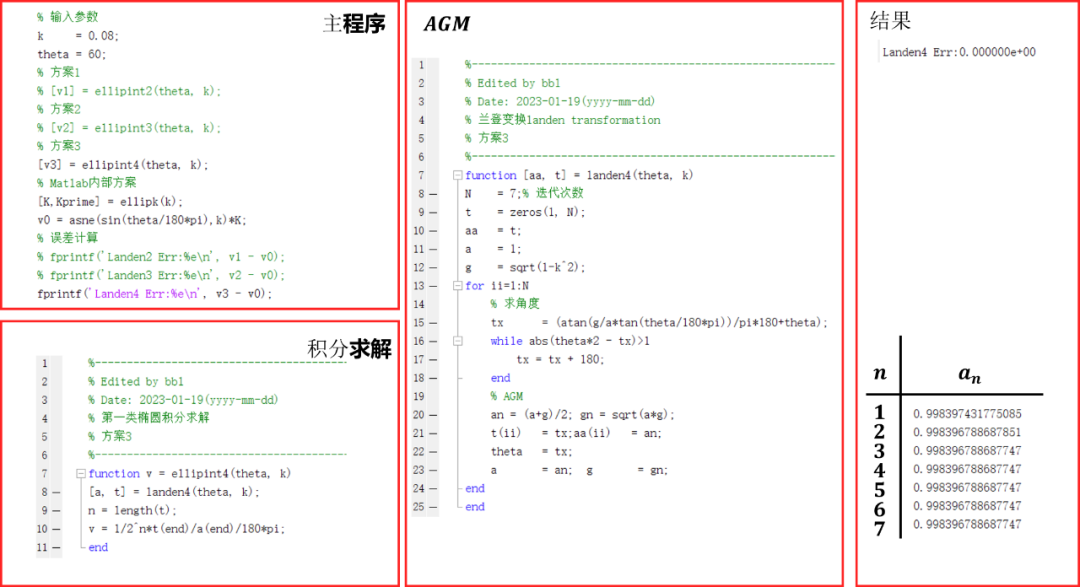
和Matlab原生态函数计算结果完全一样, 误差为0。

雅可比椭圆函数数值计算

方案1(AGM)

使用AGM可以对雅可比椭圆函数的数值计算, 也就是前述椭圆积分方案3的逆运算: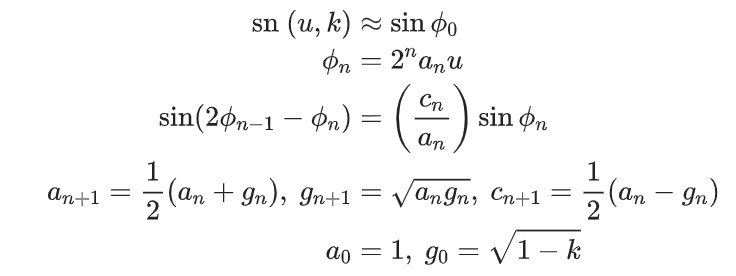

Matlab验证结果如下:

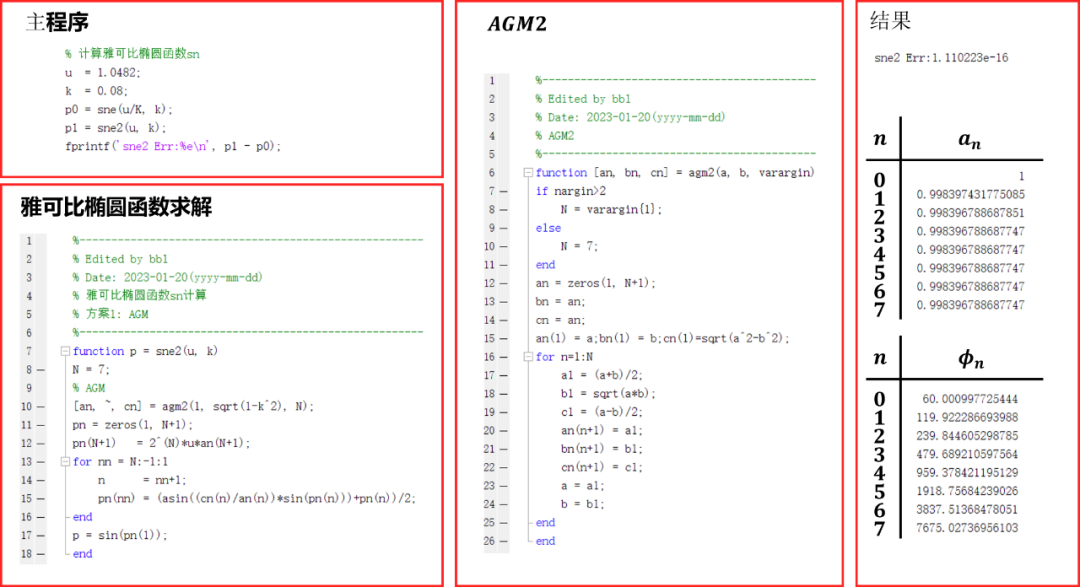
Matlab验证结果如下:

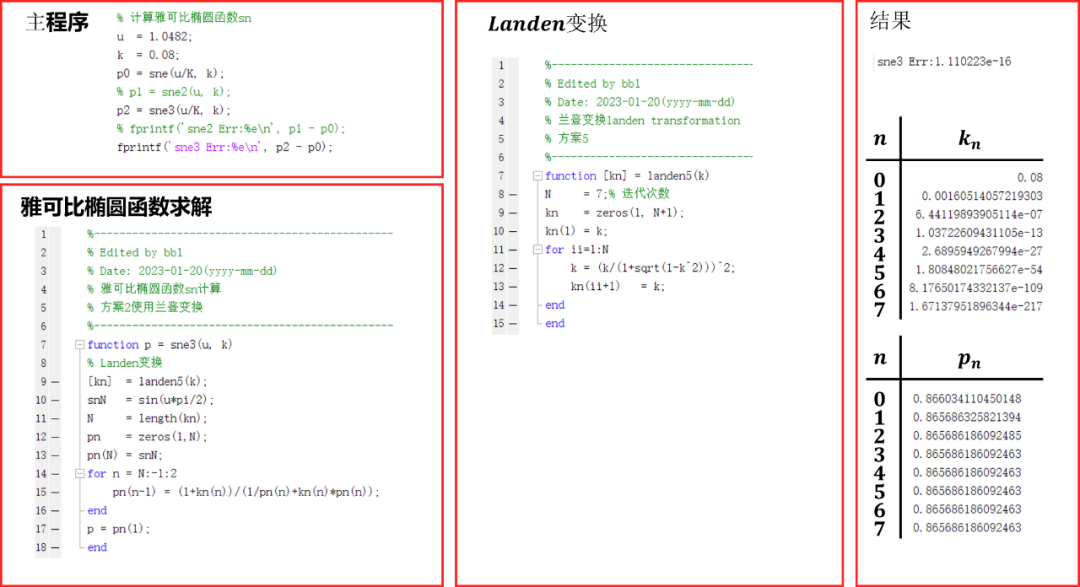
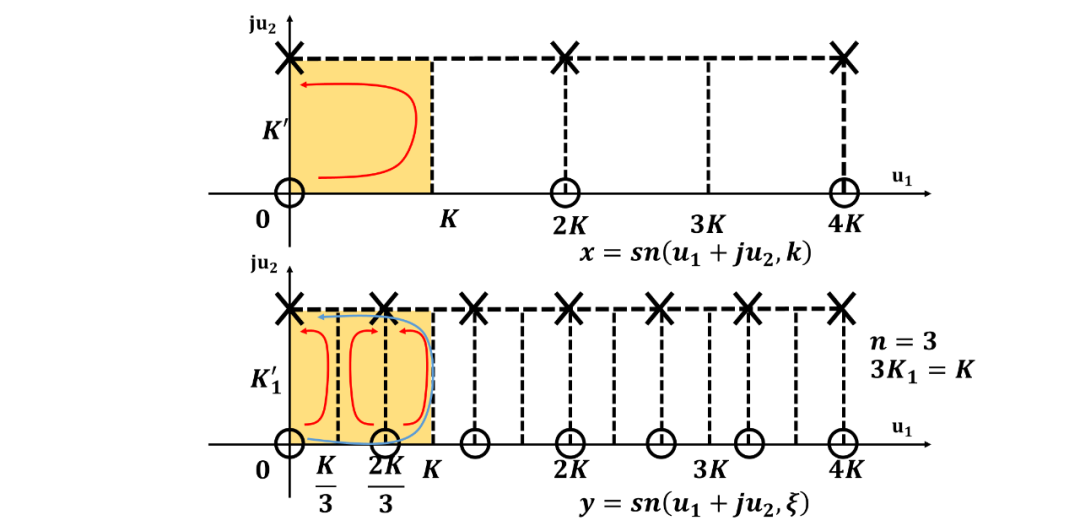
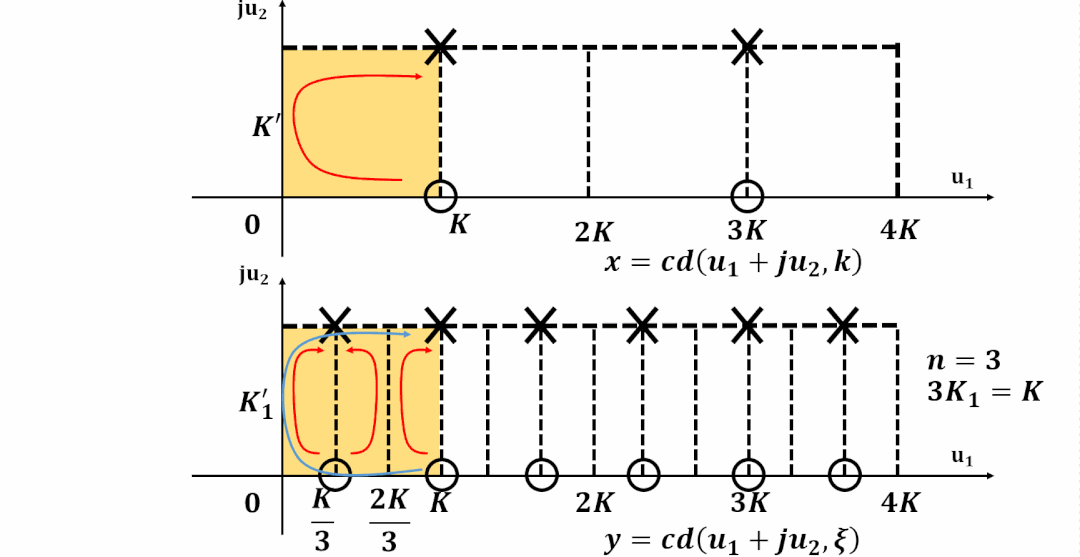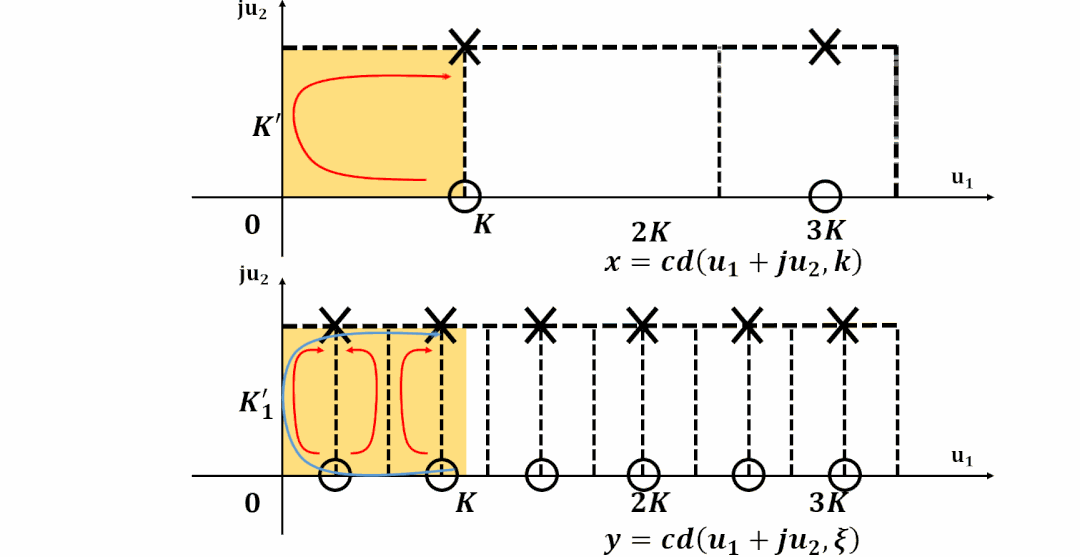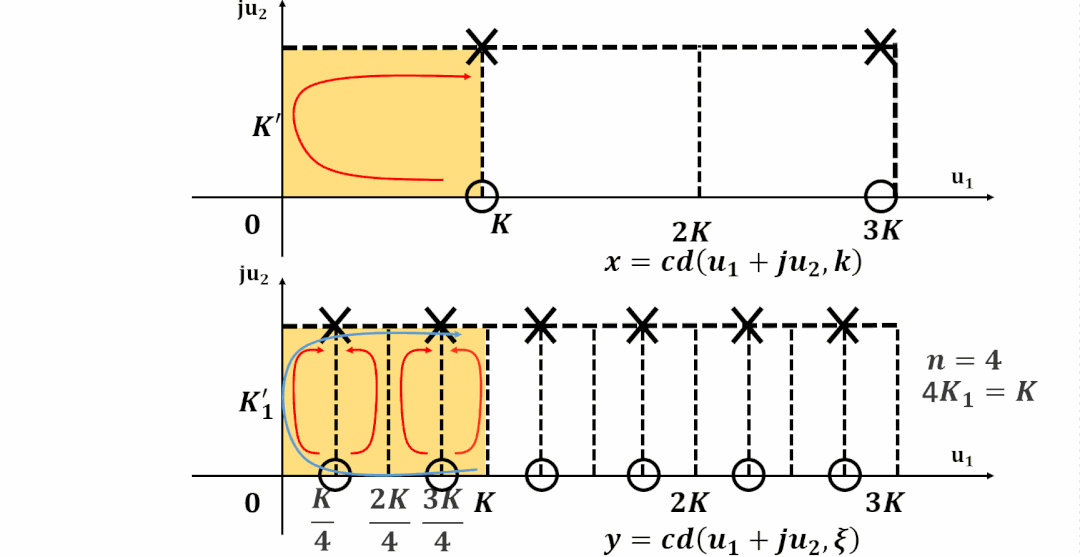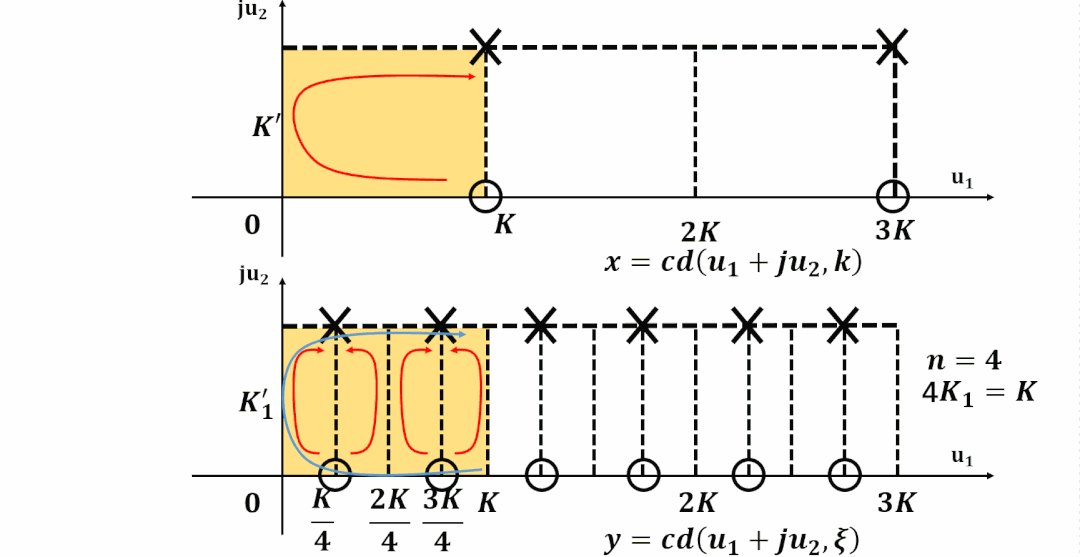
阶方程(Degree Equation)

特征方程(The Characteristic Function)

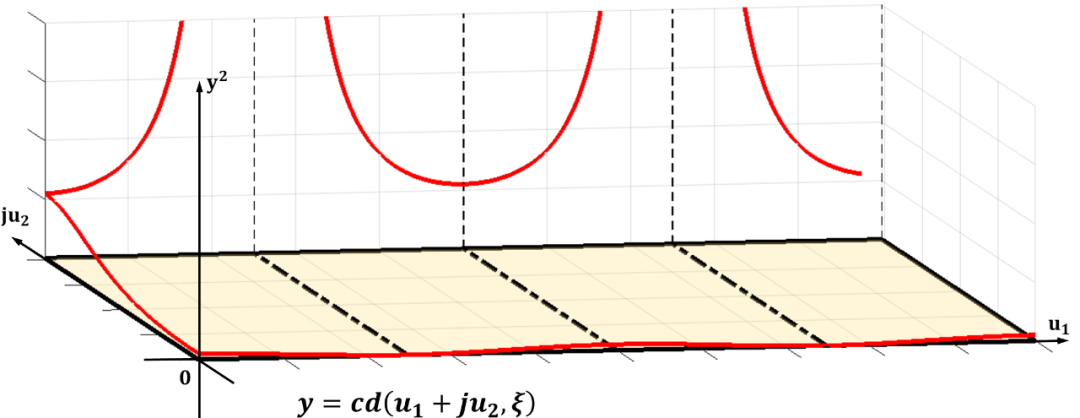
总结

本文主要对《滤波器设计中的椭圆函数》进行进一步分析和讲解, 并且建立了微分方程和椭圆滤波器特征方程之间的关系, 为后续讲解函数逼近(Approxmation)中的等纹波到微分方程之间建立联系。

审核编辑：刘清