基于OpenCL的FPGA开发设计方案

对于一个软件开发人员，可能听说过FPGA，甚至在大学课程设计中，可能拿FPGA做过计算机体系架构相关的验证，但是对于它的第一印象可能觉得这是硬件工程师干的事儿。   目前，随着人工智能的兴起，GPU 借助深度学习，走上了历史的舞台，并且正如火如荼的跑者各种各样的业务，从 training 到 inference 都有它的身影。FPGA 也借着这股浪潮，慢慢地走向数据中心，发挥着它的优势。所以接下来就讲讲 FPGA 如何能让程序员们更好友好的开发，而不需要写那些烦人的 RTL 代码，不需要使用 VCS，Modelsim 这样的仿真软件，就能轻轻松松实现 unit test。   实现这一编程思想的转变，是因为 FPGA 借助 OpenCL 实现了编程，程序员只需要通过 C/C++ 添加适当的 pragma 就能实现 FPGA 编程。为了让您用 OpenCL 实现的 FPGA 应用能够有更高的性能，您需要熟悉如下介绍的硬件。另外，将会介绍编译优化选项，有助于将您的 OpenCL 应用更好的实现 RTL 的转换和映射，并部署到 FPGA 上执行。  

FPGA 概览

FPGA 是高规格的集成电路，可以实现通过不断的配置和拼接，达到无限精度的函数功能，因为它不像 CPU 或者 GPU 那样，基本数据类型的位宽都是固定的，相反 FPGA 能够做的非常灵活。在使用 FPGA 的过程中，特别适合一些 low-level 的操作，比如像 bit masking、shifting、addition 这样的操作都可以非常容易的实现。  

为了达到并行化计算，FPGA 内部包含了查找表（LUTs），寄存器（register），片上存储（on-chip memory）以及算术运算硬核（比如数字信号处理器 (DSP) 块）。这些 FPGA 内部的模块通过网络连接在一起，通过编程的手段，可以对连接进行配置，从而实现特定的逻辑功能。这种网络连接可重配的特性为 FPGA 提供了高层次可编程的能力。（FPGA的可编程性就体现在改变各个模块和逻辑资源之间的连接方式）   举个例子，查找表（LUTs）体现的 FPGA 可编程能力，对于程序猿来说，可以等价理解为一个存储器（RAM）。

对于 3-bits 输入的 LUT 可以等价理解为一个拥有 3位地址线并且 8 个 1-bit 存储单元的存储器（一个8长度的数组，数组内每个元素是 1bit）。那么当需要实现 3-bits 数字按位与操作的时候，8长度数组存的是 3-bits 输入数字的按位与结果，一共是 8 种可能性。当需要实现 3-bits 按位异或的时候，8长度数组存的是 3-bits 输入数字的按位异或结果，一共也是 8 种可能性。这样，在一个时钟周期内，3-bits 的按位运算就能够获取到，并且实现不同功能的按位运算，完全是可编程的（等价于修改 RAM 内的数值）。   3-bits 输入 LUT 实现按位与（bit-wise AND）示例：

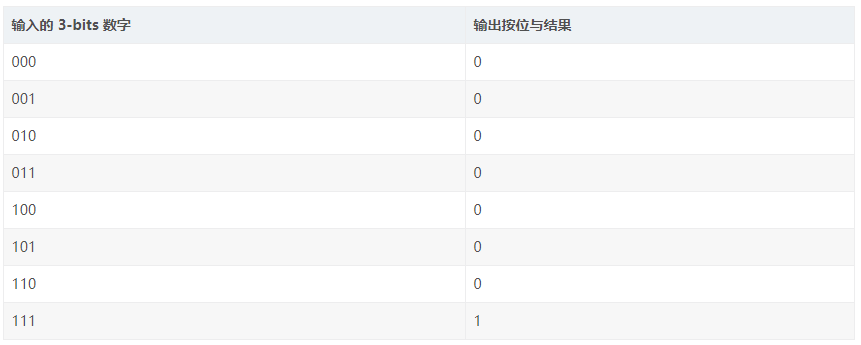
注：3-bits 输入 LUT 查找表   我们看到的三输入的按位与操作，如下所示，在 FPGA 内部，可通过 LUT 实现。  

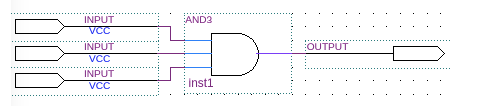
  如上展示了 3输入，1输出的 LUT 实现。当将 LUT 并联，串联等方式结合起来后就可以实现更加复杂的逻辑运算了。   传统 FPGA 开发   ▍传统 FPGA 与软件开发对比   对于传统的 FPGA 开发与软件开发，工具链可以通过下表简单对比：  

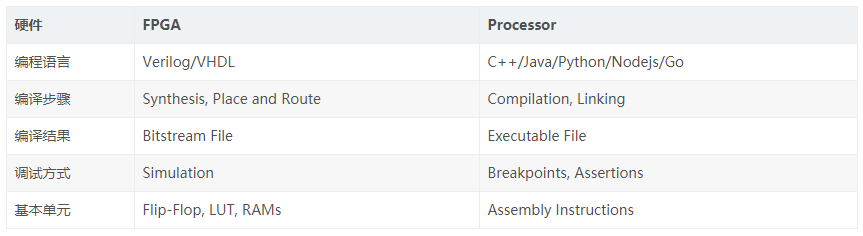
注：传统 FPGA 与软件开发对比表   重点介绍一下，编译阶段的 Synthesis (综合)，这部分与软件开发的编译有较大的不同。一般的处理器 CPU、GPU等，都是已经生产出来的 ASIC，有各自的指令集可以使用。但是对于 FPGA，一切都是空白，有的只是零部件，什么都没有，但是可以自己创造任何结构形式的电路，自由度非常的高。这种自由度是 FPGA 的优势，也是开发过程中的劣势。   写到这里，让我想起了最近 《神秘的程序员们》中的一个梗：

 

 

 

注：漫画来源《神秘的程序员们56》by 西乔
传统的FPGA开发就像10岁时候的 Linux，想吃一个蛋糕，需要自己从原材料开始加工。FPGA 正是这种状态，想要实现一个算法，需要写 RTL，需要设计状态机，需要仿真正确性。   ▍传统 FPGA 开发方式   复杂系统，需要使用有限状态机（FSM），一般就需要设计下图包含的三部分逻辑：组合电路，时序电路，输出逻辑。通过组合逻辑获取下一个状态是什么，时序逻辑用于存储当前状态，输出逻辑混合组合、时序电路，得到最终输出结果。  

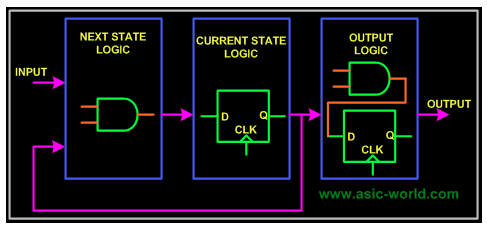
  然后，针对具体算法，设计逻辑在状态机中的流转过程：  

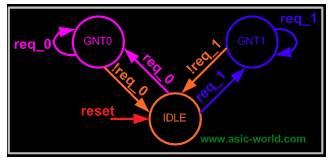
  实现的 RTL 是这样的：
 

 

module fsm_using_single_always (
clock      , // clockreset      , // Active high, syn resetreq_0      , // Request 0req_1      , // Request 1gnt_0      , // Grant 0gnt_1      
);//=============Input Ports=============================input   clock,reset,req_0,req_1; //=============Output Ports===========================output  gnt_0,gnt_1;//=============Input ports Data Type===================wire    clock,reset,req_0,req_1;//=============Output Ports Data Type==================reg     gnt_0,gnt_1;//=============Internal Constants======================parameter SIZE = 3           ;
parameter IDLE  = 3'b001,GNT0 = 3'b010,GNT1 = 3'b100 ;//=============Internal Variables======================reg   [SIZE-1:0]          state        ;// Seq part of the FSMreg   [SIZE-1:0]          next_state   ;// combo part of FSM//==========Code startes Here==========================always @ (posedge clock)begin : FSMif (reset == 1'b1) begin
 state <= #1 IDLE;
 gnt_0 <= 0;
 gnt_1 <= 0;end else
case(state)
  IDLE : if (req_0 == 1'b1) begin
               state <= #1 GNT0;
               gnt_0 <= 1;              end else if (req_1 == 1'b1) begin
               gnt_1 <= 1;
               state <= #1 GNT1;              end else begin
               state <= #1 IDLE;              end
  GNT0 : if (req_0 == 1'b1) begin
               state <= #1 GNT0;              end else begin
               gnt_0 <= 0;
               state <= #1 IDLE;              end
  GNT1 : if (req_1 == 1'b1) begin
               state <= #1 GNT1;              end else begin
               gnt_1 <= 0;
               state <= #1 IDLE;              end
  default : state <= #1 IDLE;
endcaseendendmodule // End of Module arbiter

  传统的 RTL 设计，对于程序员简直就是噩梦啊，梦啊，啊～～～工具链完全不同，开发思路完全不同，还要分析时序，一个 Clock 节拍不对，就要推翻重来，重新验证，一切都显得太底层，不是很方便。那么，这些就交给专业的 FPGAer 吧，下面介绍的 OpenCL 开发 FPGA，有点像 25 岁的 Linux 了。有了高层次的抽象。用起来自然也会更加方便。  
▍基于 OpenCL 的 FPGA 开发
  OpenCL 对于 FPGA 开发，注入了新鲜的血液，一种面向异构系统的编程语言，将 FPGA 最为异构实现的一种可选设备。由 CPU Host 端控制整个程序的执行流程，FPGA Device 端则作为异构加速的一种方式。异构架构，有助于解放 CPU，将 CPU 不擅长的处理方式，下发到 Device 端处理。目前典型的异构 Device 有：GPU、Intel Phi、FPGA。   OpenCL 是个 what？   注：引用自 wiki
Open Computing Language (OpenCL) is a framework for writing programs that execute across heterogeneousplatforms consisting of central processing units (CPUs), graphics processing units (GPUs), digital signal processors(DSPs), field-programmable gate arrays (FPGAs) and other processors or hardware accelerators. OpenCL specifies aprogramming language (based on C99) for programming these devices and application programming interfaces (APIs) to control the platform and execute programs on the compute devices. OpenCL provides a standard interface for parallel computing using task-based and data-based parallelism.   大意是说：OpenCL 是一个用于异构平台编程的框架，主要的异构设备有 CPU、GPU、DSP、FPGA以及一些其它的硬件加速器。OpenCL 基于 C99 来开发设备端代码，并且提供了相应的 API 可以调用。OpenCL 提供了标准的并行计算的接口，以支持任务并行和数据并行的计算方式。  
OpenCL 案例分析  
这里采用 Altera 官网的矩阵乘法案例进行分析。可以通过如下链接下载案例：Altera OpenCL Matrix Multiplication   代码结构如下：
 

.|-- common|   |-- inc|   |   `-- AOCLUtils|   |       |-- aocl_utils.h|   |       |-- opencl.h|   |       |-- options.h|   |       `-- scoped_ptrs.h|   |-- readme.css|   `-- src|       `-- AOCLUtils|           |-- opencl.cpp|           `-- options.cpp`-- matrix_mult
   |-- Makefile
   |-- README.html
   |-- device
   |   `-- matrix_mult.cl
   `-- host
       |-- inc
       |   `-- matrixMult.h
       `-- src
           `-- main.cpp

    其中，和 FPGA 相关的代码是 matrix_mult.cl ，该部分代码描述了 kernel 函数，这部分函数会通过编译器生成 RTL 代码，然后 map 到 FPGA 电路中。   kernel 函数的定义如下：
 

__kernel
__attribute((reqd_work_group_size(BLOCK_SIZE,BLOCK_SIZE,1)))
__attribute((num_simd_work_items(SIMD_WORK_ITEMS)))void matrixMult( __global float *restrict C, 
                __global float *A, 
                __global float *B, 
                int A_width, 
                int B_width)

    模式比较固定，需要注意的是 __global 指明从 CPU 传过来的数据，存放到全局内存中，可以是 FPGA 片上存储资源，DDR，QDR 等，这个视 FPGA 的 OpenCL BSP 驱动，会有所区别。num_simd_work_items 用于指明 SIMD 的宽度。reqd_work_group_size 指明了工作组的大小。这些概念，可以参考 OpenCL 的使用手册。

  函数实现如下：

 

// 声明本地存储，暂存数组的某一个 BLOCK__local float A_local[BLOCK_SIZE][BLOCK_SIZE];
__local float B_local[BLOCK_SIZE][BLOCK_SIZE];// Block indexint block_x = get_group_id(0);int block_y = get_group_id(1);// Local ID index (offset within a block)int local_x = get_local_id(0);int local_y = get_local_id(1);// Compute loop boundsint a_start = A_width * BLOCK_SIZE * block_y;int a_end   = a_start + A_width - 1;int b_start = BLOCK_SIZE * block_x;float running_sum = 0.0f;for (int a = a_start, b = b_start; a <= a_end; a += BLOCK_SIZE, b += (BLOCK_SIZE * B_width))
{  // 从 global memory 读取相应 BLOCK 数据到 local memory
 A_local[local_y][local_x] = A[a + A_width * local_y + local_x];
 B_local[local_x][local_y] = B[b + B_width * local_y + local_x];  // Wait for the entire block to be loaded.
 barrier(CLK_LOCAL_MEM_FENCE);  // 计算部分，将计算单元并行展开，形成乘法加法树
 #pragma unroll
 for (int k = 0; k < BLOCK_SIZE; ++k)
 {
   running_sum += A_local[local_y][k] * B_local[local_x][k];
 }  // Wait for the block to be fully consumed before loading the next block.
 barrier(CLK_LOCAL_MEM_FENCE);
}// Store result in matrix CC[get_global_id(1) * get_global_size(0) + get_global_id(0)] = running_sum;

  采用 CPU 模拟仿真 FPGA  
对其进行仿真，不需要 programer 关心具体的时序是怎么走的，只需要验证逻辑功能就可以，Altera OpenCL SDK 提供了 CPU 仿真 Device 设备的功能，采用如下方式进行：
 

# To generate a .aocx file for debugging that targets a specific accelerator board$ aoc -march=emulator device/matrix_mult.cl -o bin/matrix_mult.aocx --fp-relaxed --fpc --no-interleaving default --board # Generate Host exe.$ make# To run the application$ env CL_CONTEXT_EMULATOR_DEVICE_ALTERA=8 ./bin/host -ah=512 -aw=512 -bw=512

  上述脚本中，通过 -march=emulator 设置创建一个可用于 CPU debug 的设备可执行文件。-g 添加调试 flag。—board 用于创建适配该设备的 debugging 文件。CL_CONTEXT_EMULATOR_DEVICE_ALTERA 为用于 CPU 仿真的设备数量。   当执行上述脚本后，输出如下：

  $ env CL_CONTEXT_EMULATOR_DEVICE_ALTERA=8 ./bin/host -ah=512 -aw=512 -bw=512Matrix sizes:
 A: 512 x 512
 B: 512 x 512
 C: 512 x 512Initializing OpenCL
Platform: Altera SDK for OpenCL
Using 8 device(s)
 EmulatorDevice : Emulated Device
 ...
 EmulatorDevice : Emulated Device
Using AOCX: matrix_mult.aocx
Generating input matrices
Launching for device 0 (global size: 512, 64)
...
Launching for device 7 (global size: 512, 64)

Time: 5596.620 ms
Kernel time (device 0): 5500.896 ms
...
Kernel time (device 7): 5137.931 ms

Throughput: 0.05 GFLOPS

Computing reference output
Verifying
Verification: PASS
通过仿真时候设置 Device ＝ 8，模拟 8 个设备运行 (512, 512) * (512, 512) 规模的矩阵，最终验证正确。接下来就可以将其真正编译到 FPGA 设备上后运行。   FPGA 设备上运行矩阵乘   这个时候，真正要将代码下载到 FPGA 上执行了，这时候，只需要做一件事，那就是用 OpenCL SDK 提供的编译器，将 *.cl 代码适配到 FPGA 上，执行编译命令如下：
$ aoc device/matrix_mult.cl -o bin/matrix_mult.aocx --fp-relaxed --fpc --no-interleaving default  --board   这个过程比较慢，一般需要几个小时到10几个小时，视 FPGA 上资源大小而定。（目前这部分时间太长暂时无法解决，因为这里的编译，其实是在行程一个能够正常工作的电路，软件会进行布局布线等工作）   等待编译完成后，将生成的 matrix_mult.aocx文件烧写到 FPGA 上就 ok 啦。   烧写的命令如下：
 

$ aocl program  matrix_mult.aocx

  这时候，大功告成，可以运行 host 端程序了：
 

$ ./host -ah=512 -aw=512 -bw=512Matrix sizes:
 A: 512 x 512
 B: 512 x 512
 C: 512 x 512Initializing OpenCL
Platform: Altera SDK for OpenCL
Using 1 device(s)
  : Altera OpenCL QPI FPGA
Using AOCX: matrix_mult.aocx
Generating input matrices
Launching for device 0 (global size: 512, 512)


Time: 2.253 ms
Kernel time (device 0): 2.191 ms


Throughput: 119.13 GFLOPS


Computing reference output
Verifying
Verification: PASS

  可以看到，矩阵乘法能够在 FPGA 上正常运行，吞吐大概在 119GFlops 左右。  

小结

从上述的开发流程，OpenCL 大大的解放了 FPGAer 的开发周期，并且对于软件开发者，也比较容易上手。这是他的优势，但是目前开发过程中，还是存在一些问题，如：编译器优化不足，相比 RTL 写的性能存在差距；编译到 Device 端时间太长。不过这些随着行业的发展，一定会慢慢的进步。    编辑：黄飞