

卡尔曼滤波器介绍与理论分析(上)
模拟技术
描述
最近业余在研究物体追踪,看到传统的方法用到了卡尔曼滤波(Kalman Filter)+匈牙利算法做轨迹匹配,因而开始研究这两种算法是如何实现的。这里简单总结一下卡尔曼滤波算法探索的过程。
▊ 卡尔曼滤波的背景
卡尔曼滤波常用于动态多变化系统中的状态估计,是一种通用性强的自回归滤波器。它的由来和NASA登月有关。其发明者鲁道夫.E.卡尔曼在一次访问NASA的时候,发现阿波罗计划中一个难点是轨道预测问题,因而提出了一种滤波器,可以帮助高效预测轨迹,辅助导航。NASA最终使用了这个滤波器,然后成功实现人类第一次登月计划。卡尔曼滤波器由此得名。
卡尔曼滤波器可以用来估计不确定信息,并给出状态量下一时刻的情况。即便在有噪声干扰的情况下,也可以较好的预测下一状态的情况,并找出多变量间不易察觉的相关性。因而卡尔曼滤波器可以很好适应不断变化的系统,并且 内存占用量低,推理速度快,比较适合资源受限制的场景 。
▊ 卡尔曼滤波介绍
先来看一个简单的问题。考虑一辆车在道路上行驶,他的状态和运行速度,位置信息相关,用向量表示为:
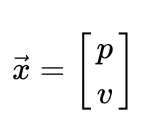
其中 p 变量对应位置 v 变量对应速度,都为随机变量且符合正态分布,每个分布都有一个均值(正太分布的中心)和对应的方差 .(衡量变量的不确定性)。
那么卡尔曼滤波是怎么工作的呢?我们还是回到刚才的例子。上面例子中的这两个变量看起来没有明显的对应关系,也就是说,给定速度,没法准确定出位置。
但是如果我们知道位置和速度的初始信息,其实是有办法将两个变量联系起来的。假设车辆一直保持匀速行驶,通过下面的公式其实就可以(要注意的是,换成其他问题,我们不一定能意识到这个公式的存在)
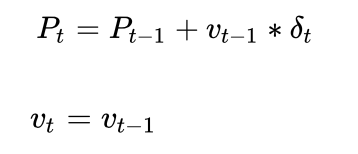
基于上面的公式,我们可以直观的定义当前时刻和上一时刻之间的对应关系;假定系统中所有状态量为
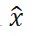
,对应的有

这里我们称
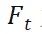
为预测矩阵,也会用
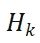
表示,预测矩阵的目的是刻画从上一状态到当前状态对应的关系。
这也就是卡尔曼滤波的目标。我们希望从不确定的系统中,尽可能的发掘出确定的信息。那么另一个问题是,如何知道有多少确定(不确定)的信息可以发掘呢?我们需要一个指标来衡量系统的不确定性。
回到上个例子中,位置和速度的关系其实是不确定的,但是却是有相关性的,只是不能直观的看出来。那么如何衡量这种相关性呢?其中一个办法就是使用协方差矩阵,来衡量两个变量的相关程度。给定
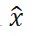
,对应的协方差矩阵p为
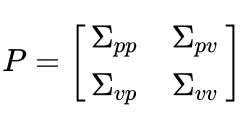
考虑到预测矩阵的影响,给定上一时刻的
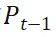
,对应可以更新为
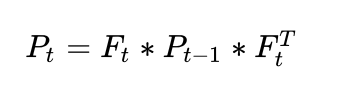
由此便解决了理想情况下卡尔曼滤波如何做预测的问题。但是实际情况下,系统中可能还是存在干扰或者噪声因素。比如车辆行驶过程中,遇到雨天路滑则需要减速慢行,这种情况下道路状况会作为外部因素,干扰系统行为和决策。因为针对变化量
,会额外追加一个控制变量来建模外部因素。
假设行车遇到雨天需要减速,我们考虑了运动时刻的车辆加速度a为外部影响,那么有,
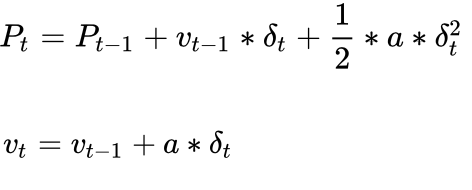
对比之前计算状态的关系式,可以发现新引入的状态对系统产生了影响,因而记为
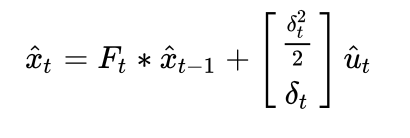
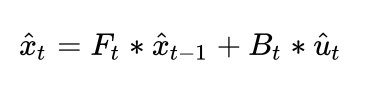
同时我们使用
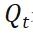
表示,引入的外部因素对于协方差的影响,因而有
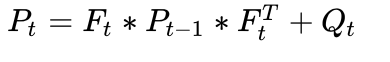
这里总结一下,新引入的外部变量使得
1)当前的最佳估计不再为系统自身的最佳估计,还考虑了外部因素影响
2)当前的不确定性不再为系统自身的不确定性,引入了外部的不确定性做参考
-
卡尔曼滤波器原理分析2023-05-09 1850
-
卡尔曼滤波器介绍与理论分析(下)2023-02-10 809
-
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程2022-12-15 4429
-
扩展卡尔曼滤波的原理2022-08-12 7045
-
卡尔曼滤波器是什么2021-11-16 1510
-
MATLAB在卡尔曼滤波器中应用的理论与实践Kalma(英文版)2021-10-18 917
-
卡尔曼滤波器的使用原理2021-08-17 1429
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1142
-
卡尔曼滤波器及其应用基础PDF电子书免费下载2020-03-13 1645
-
图解卡尔曼滤波器2018-02-07 5047
-
卡尔曼滤波器参数分析与应用方法研究2016-06-21 863
-
卡尔曼滤波器在入侵检测中的应用2009-08-06 500
-
卡尔曼滤波器原理2008-07-14 1293
全部0条评论

快来发表一下你的评论吧 !

