卡尔曼滤波器介绍与理论分析（下）

▊ 卡尔曼滤波公式推导

通过预测状态量和不确定性，我们可以有较大把握预测对某一时刻下的状态。到目前为止，我们很好地完成了对系统的建模，但是有一个问题没有考虑到，那就是系统的初始值怎么得到。

对于系统中数据的收集，我们一般基于传感器来实现。但是同一传感器在同一时刻，可能因为外部原因导致收集得到的信号不完全一样。因而系统输入初始值对应结果大概率有很多噪音。这里我们把收集数据的均值记为, 方差记为

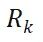
现在就有了新的问题。对于当前时刻，我们有了两组参考值，一组是预测值，一组是测量值。也许两组都对，也许其中只有一组对，也可能都不准（比如传感器测得不直接，偏差太大；预测值也偏差太大）。这种情况下，应该如何得到最终结果呢？

其中一个方案是，考虑直接融合两组结果。我们假设这两组数据都是正态分布，因而直接取pdf相乘就可以得到一个新的分布，也就是做一个联合概率分布的计算。这个联合概率分布本质上计算了前后状态转化对应分布和输入输出状态分布联合作用下的结果。

因而我们有下式

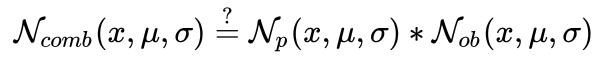
这里要注意的是，两个高斯pdf的乘积不是一个pdf（概率加和明显不是1），但是正比于一个未知高斯分布，因而我们可以求得这个新分布的均值和方差，根据如下关系，

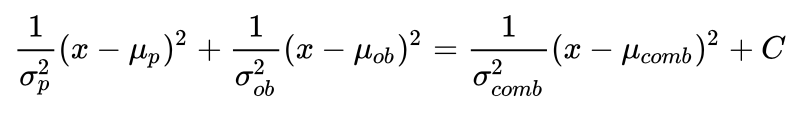
为了使其成立，我们需要保证：

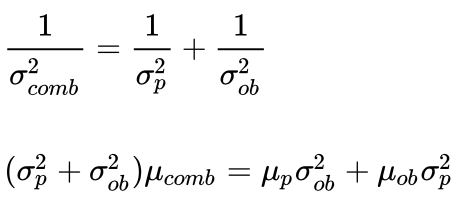
联立二式并稍作变化，我们得到：

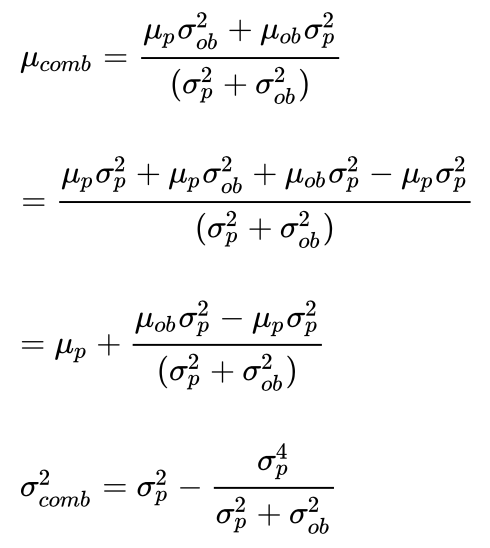
令

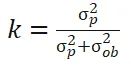
为卡尔曼增益， 我们有

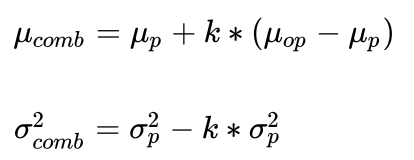
对应的矩阵形式为：

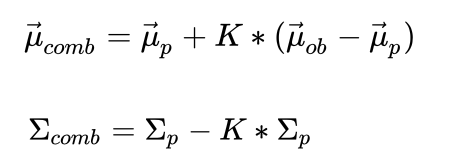
这里为了防止混淆，先停下来总结一下，

1)我们介绍了预测变量，下标为p，分布均值，方差

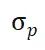
分别对应于

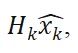
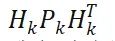
2)我们介绍了观测变量，下标为ob，分布均值记为

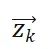
, 方差记为

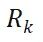
3)基于1，2，我们代入即可推导出完整的卡尔曼滤波公式

所以根据刚才列出的计算式分别代入，我们可以得到，

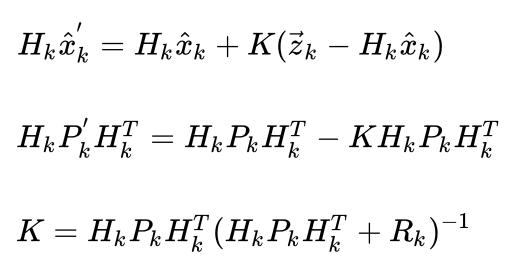
进而可以求解得状态更新方程和卡尔曼增益求解公式:

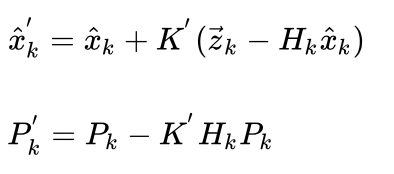
注意这里的卡尔曼增益更新为

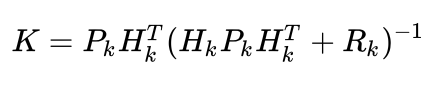
至此，便可以套公式更新卡尔曼滤波的参数了。

▊ 总结

卡尔曼滤波是处理线性系统非常好用的工具，对于不确定性的建模取自于物理、机械模型，所以对于现实生活中的状态还是能很好把握的。对于非线性系统，拓展卡尔曼滤波(extended Kalman filter)也可以做到很好地处理。

本文通过现实场景建模引入问题，简单介绍了卡尔曼滤波算法，对于更加清楚的公式推导请见参考列出的几篇相关文章。

欢迎大家在下方留言或者将建议发到我的邮箱([e-mail])，以便更好地交流心得。另外感谢参考文献所列诸作者。

参考文献:

. 论智：图说卡尔曼滤波，一份通俗易懂的教程

(https://zhuanlan.zhihu.com/p/39912633)

. 涅索斯衬衫：卡尔曼滤波（Kalman Filter）原理与公式推导

(https://zhuanlan.zhihu.com/p/48876718)