

卡曼滤波器实现多目标跟踪解析 2
电子说
1.4w人已加入
描述
通过测量来细化估计值
我们可能有好几个传感器,它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点,它可以读取位置,可以读取速度,重点是,它能告诉我们关于状态的间接信息——它是状态下产生的一组读数。
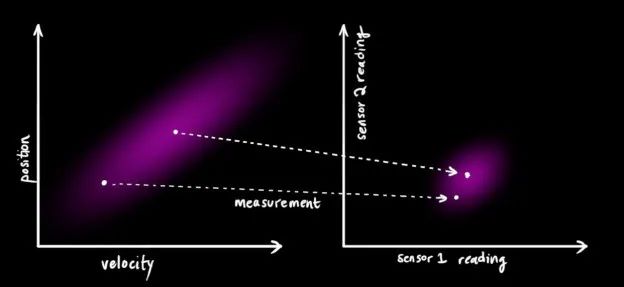
请注意,读数的规模和状态的规模不一定相同,所以我们把传感器读数矩阵设为
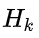
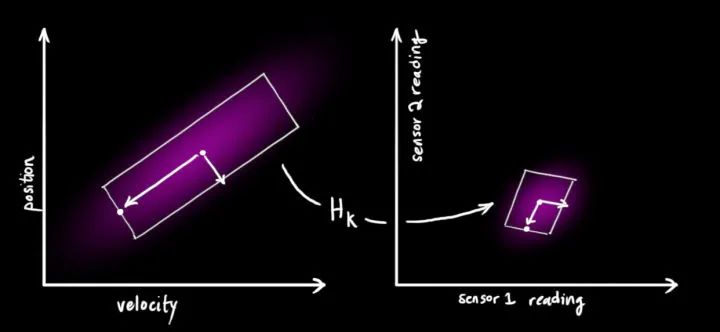
把这些分布转换为一般形式
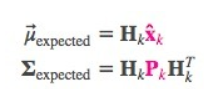
卡尔曼滤波的一大优点是擅长处理传感器噪声。换句话说,由于种种因素,传感器记录的信息其实是不准的,一个状态事实上可以产生多种读数。
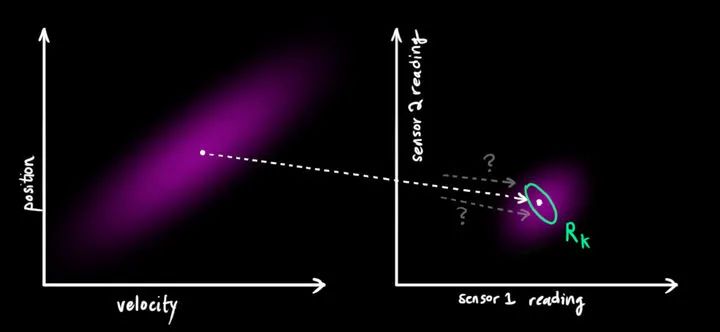
我们将这种不确定性(即传感器噪声)的协方差设为
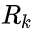
,读数的分布均值设为
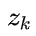
。现在我们得到了两块高斯分布,一块围绕预测的均值,另一块围绕传感器读数。
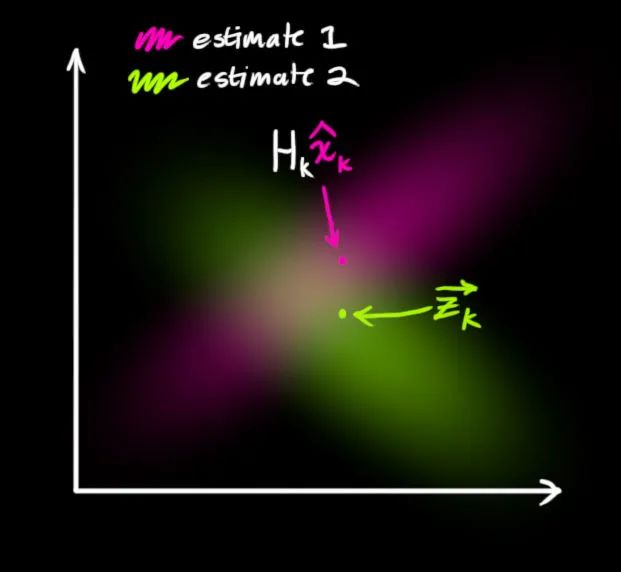
如果要生成靠谱预测,模型必须调和这两个信息。也就是说,对于任何可能的读数
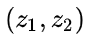
,这两种方法预测的状态都有可能是准的,也都有可能是不准的。重点是我们怎么找到这两个准确率。最简单的方法是两者相乘:
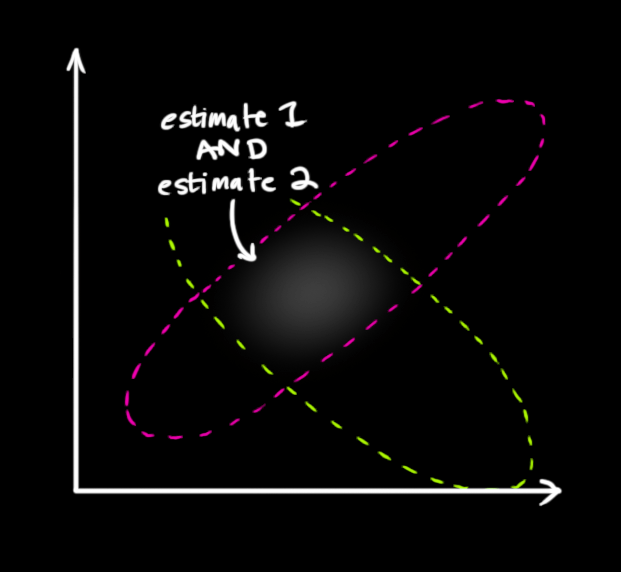
两块高斯分布相乘后,我们可以得到它们的重叠部分,这也是会出现最佳估计的区域。换个角度看,它看起来也符合高斯分布:
事实证明,当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时,你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了:我们必须有一个公式来从旧的参数中获取这些新参数!
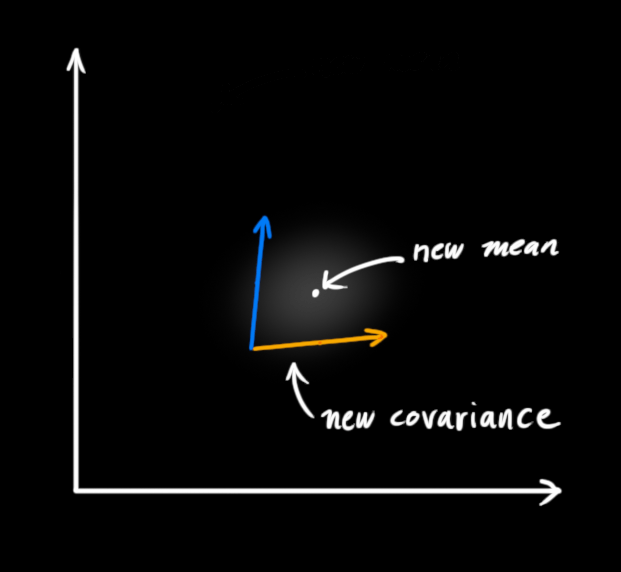
结合高斯
两条高斯曲线相乘
按照一维方程进行扩展,可得
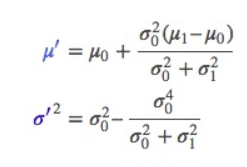
用k简化一下
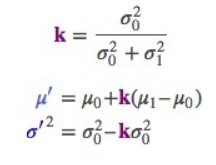
以上是一维的内容,如果是多维空间,把这个式子转成矩阵格式
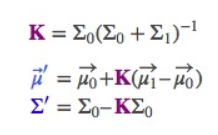
这个矩阵
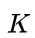
就是我们说的卡尔曼增益
结合在一起
截至目前,我们有用矩阵
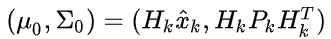
预测的分布,有用传感器读数
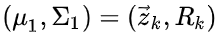
预测的分布。把它们代入上节的矩阵等式中:
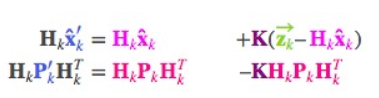
相应的,卡尔曼增益就是:
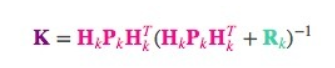
考虑到
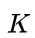
里还包含着一个
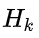
,我们再精简一下上式
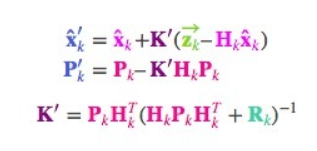
最后,
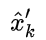
是我们的最佳估计值,我们可以把它继续放进去做另一轮预测
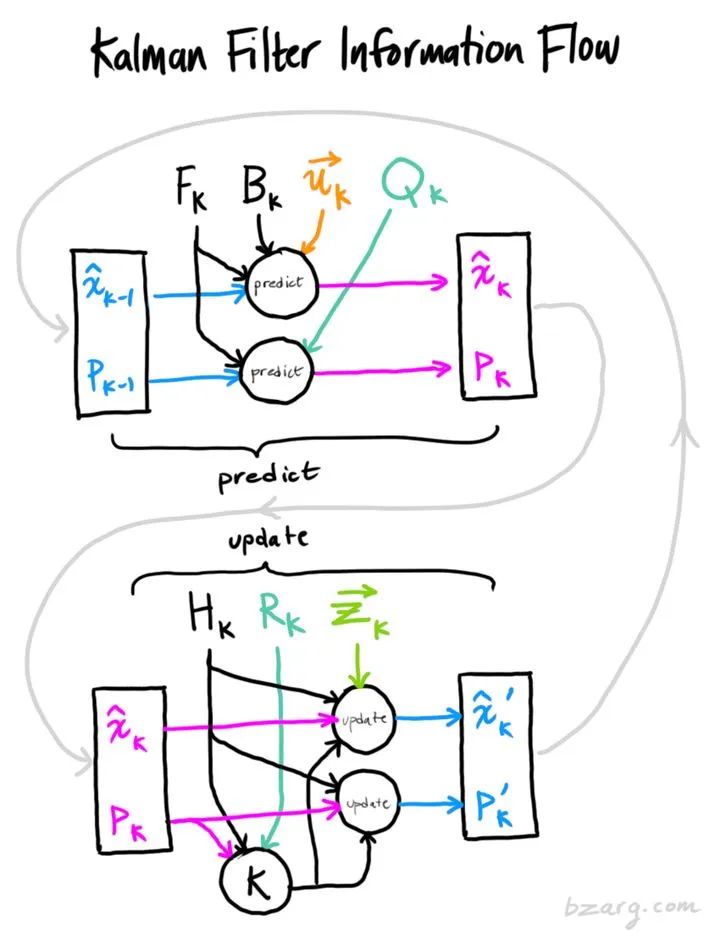
4 代码实现
In [9]
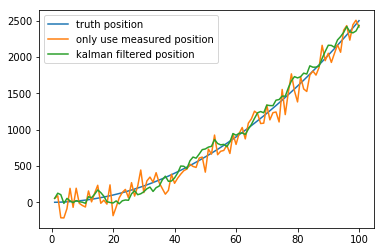
import matplotlib.pyplot as plt# 模拟数据t = np.linspace(1,100,100)# print(t)a = 0.5position = (a * t**2)/2# print(position)position_noise = position+np.random.normal(0,120,size=(t.shape[0])) plt.plot(t,position,label='truth position') # 原值plt.plot(t,position_noise,label='only use measured position') # 加入噪声的值# 初始的估计的位置就直接用GPS测量的位置predicts = [position_noise[0]]position_predict = predicts[0]predict_var = 0odo_var = 120**2 #这是我们自己设定的位置测量仪器的方差,越大则测量值占比越低v_std = 50 # 测量仪器的方差for i in range(1,t.shape[0]): dv = (position[i]-position[i-1]) + np.random.normal(0,50) # 模拟从惯性测量单元IMU读取出的速度 position_predict = position_predict + dv # 利用上个时刻的位置和速度预测当前位置 predict_var += v_std**2 # 更新预测数据的方差 # 下面是Kalman滤波 position_predict = position_predict*odo_var/(predict_var + odo_var)+position_noise[i]*predict_var/(predict_var + odo_var) predict_var = (predict_var * odo_var)/(predict_var + odo_var)**2 predicts.append(position_predict) plt.plot(t,predicts,label='kalman filtered position') # 滤波后的值plt.legend()plt.show()# 卡尔曼滤波将噪声值(橙色线),滤波后(绿色线),尽量去拟合原值(蓝色线)
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
卡尔曼滤波器的特性及仿真2024-11-04 1447
-
基于扩展卡尔曼滤波的机动目标航迹跟踪2023-02-15 574
-
卡曼滤波器实现多目标跟踪解析 12023-02-10 1680
-
如何使用FPGA实现纯方位目标跟踪的伪线性卡尔曼滤波器2021-03-10 887
-
GM-PHD滤波器的多目标跟踪2018-03-07 1958
-
基于霍夫-无迹卡尔曼滤波的目标检测与跟踪2013-08-19 916
-
卡尔曼滤波在被动目标跟踪系统中的应用2012-04-18 1426
全部0条评论

快来发表一下你的评论吧 !

