

卡曼滤波器入门教程概述
模拟技术
描述
关于本教程
卡尔曼滤波器是一个简单的话题,然而,许多书籍和教程却把它讲的很复杂,要读懂它们需要有深厚的数学背景,并且缺乏实际的例子,几乎每一本书籍或教程都把核心思想简单明了的卡曼滤波讲得比原本更加复杂。
所以,我决定写一个简单且直观的教程并附带一些实际应用例子。 一些例子来自雷达通信领域,在该领域卡尔曼滤波被广泛使用(主要用于目标跟踪)。然而,这里提出的原理可以应用于任何需要估计和预测的领域。本教程包括三个部分:
- 第1部分通过八个数值示例介绍卡尔曼滤波器,这部分不需要先验数学知识,本教程提供了所有必要的数学背景,包括均值、方差和标准差等,阅读第一部分后,您将能够理解卡尔曼滤波器的概念,并发展出“卡尔曼滤波器直觉”。您还将能够设计一维卡尔曼滤波器。
- 第2部分描述了多维(或多元)卡尔曼滤波器-矩阵表示的卡尔曼滤波器。这部分有点高级。需要线性代数的基本知识(仅矩阵运算)。本教程也供了这部分必要的数学背景。还包括卡尔曼滤波器的数学推导和动态系统建模。阅读第二部分后,您将能够理解卡尔曼滤波器背后的数学。您还将能够设计多维卡尔曼滤波器。
- 第3部分描述了非线性卡尔曼滤波器。这一部分对于掌握卡尔曼滤波器至关重要,因为大多数现实系统都是非线性的。目前,该部分正在编写过程中。第3部分将包括扩展卡尔曼滤波器、无中心卡尔曼滤波器和粒子滤波器。
关于卡尔曼滤波器
大多数现代系统都有许多传感器,它们根据一系列测量结果来估计隐藏(未知)状态。例如,GPS接收机提供位置和速度估计,其中位置和速度是隐藏状态,卫星信号到达的差分时间是测量值。跟踪和控制系统的最大挑战之一是在存在不确定性的情况下提供对隐藏状态的准确和精确估计。在GPS接收机中,测量不确定性取决于许多外部因素,如热噪声、大气影响、卫星位置的微小变化、接收机时钟精度等。
卡尔曼滤波器是最重要和最常见的估计算法之一。卡尔曼滤波器基于不准确和不确定的测量结果产生隐藏变量的估计。此外,卡尔曼滤波器还可以根据过去的估计预测未来的系统状态。
过滤器以Rudolf E.Kálman(1930年5月19日至2016年7月2日)的名字命名。1960年,卡尔曼发表了他的著名论文,描述了离散数据线性滤波问题的递归解。
如今,卡尔曼滤波器被用于目标跟踪(雷达)、定位和导航系统、控制系统、计算机图形学等等。
预测前置要求
在深入了解卡尔曼滤波器的解释之前,让我们首先了解预测算法的必要性。例如,让我们考虑一种雷达跟踪算法。
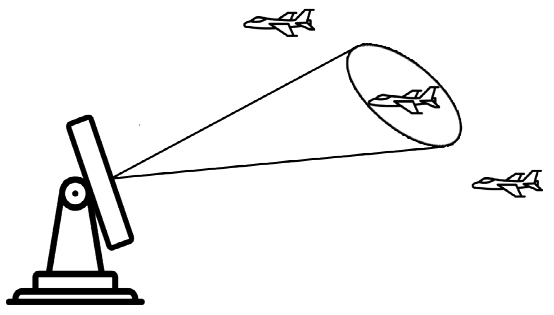
跟踪雷达向目标方向发送一束笔射束,假设追踪周期为5秒,换言之,每隔5秒,雷达通过向目标方向发送一个专用跟踪波束来重新追踪目标。发送波束后,雷达估计当前目标的位置和速度,雷达还估计(或预测)下一个追踪周期目标所处的位置。使用牛顿运动方程可以容易地计算未来目标位置:
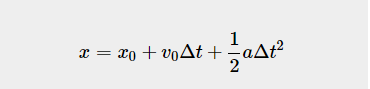
x是目标的位置x0是目标的初始位置v0是目标的初始速度a是目标的加速度Δt是时间间隔(在我们的示例中为5秒)
在三维中,牛顿的运动方程可以写成方程组:
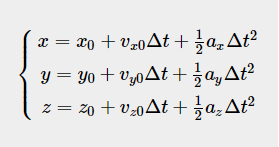
目标参数[x,y,z,vx,vy,vz,ax,ay,az]称为系统状态,当前状态是预测算法的输入,下一状态(下一时间间隔的目标参数)是算法的输出。上述方程组称为动态模型(或状态空间模型)。动态模型描述了输入和输出之间的关系。让我们回到我们的例子,如我们所见,如果当前状态和动态模型已知,则可以轻松预测下一个目标状态。然而,事实却不是这样的,首先,雷达测量值不是绝对准确的,它包括随机误差(或不确定性),误差大小取决于许多参数,例如雷达校准、波束宽度和返回回波的信噪比,测量中包含的误差称为测量噪声。此外,由于风、空气湍流和飞行员机动等外部因素,目标运动与运动方程并不严格一致,动态模型误差(或不确定性)称为过程噪声。
由于测量噪声和过程噪声,估计的目标位置可能远离实际目标位置,在这种情况下,雷达可能会将跟踪波束发送到错误的方向,从而错过目标。我们需要一种考虑过程和测量不确定性的预测算法来提高雷达跟踪性能。最广泛使用的预测算法就是
卡尔曼滤波器
。
-
卡曼滤波器入门教程数学基础12023-02-10 735
-
卡尔曼滤波器是什么2021-11-16 1516
-
卡尔曼滤波器的使用原理2021-08-17 1444
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1154
-
图解卡尔曼滤波器2018-02-07 5050
-
卡尔曼滤波器参数分析与应用方法研究2016-06-21 865
-
卡尔曼滤波器原理2008-07-14 1296
全部0条评论

快来发表一下你的评论吧 !

