

卡曼滤波器入门教程数学基础1
模拟技术
描述
揭开其背后的背景知识
在正式开始之前,我想解释几个基本术语,如方差、标准差、正态分布、估计、准确度、精度、均值、期望值和随机变量。
我希望本教程的读者都熟悉基础性的统计学知识,然而,在本教程开始时,我承诺提供必要的背景知识,以了解卡尔曼滤波器的工作原理,如果您熟悉本主题,请跳过本章并跳到下一节。
平均值和期望值
均值和期望值是密切相关的术语,然而,它们是有区别的,例如,给定五种不同的硬币——两种5美分硬币和三种10美分硬币,我们可以很容易地通过平均硬币的面值来计算平均值。
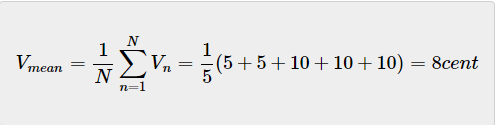
上述结果不能定义为期望值,因为系统状态(硬币值)不是隐性的,我们能够获取所有样本(所有5枚硬币)进行平均值计算。
现在假设从同一个人得到五种不同的体重测量结果:79.8kg、80kg、80.1kg、79.8kg和80.2kg,那么,人是系统,人的体重是系统状态。
由于随机测量误差的存在,导致测量结果不同,我们不知道重量的真实值,因为它是一种隐藏状态,然而,我们可以通过平均天平秤的测量值来估计其重量。

估计的结果就是体重的期望值,期望值是您期望隐藏变量在长时间或多次试验中趋向的值,平均值通常用希腊字母μ表示,字母E通常表示期望值。
方差和标准差
方差是数据集与平均值分散程度的度量,标准偏差是方差的平方根, 标准偏差用希腊字母σ(sigma)表示。因此,方差用σ2表示。
假设我们想比较两支高中篮球队球员的身高,下表提供了球员的身高和每个队的平均身高:

正如我们所看到的,两支球队的平均身高是相同的,让我们检查一下身高的方差:
由于方差度量的是数据集的分散程度,我们希望知道数据集与其平均值的方差,我们可以通过从每个变量中减去平均值来计算每个变量与平均值的距离,高度用x表示,高度的平均值用希腊字母μ表示,每个变量与平均值的距离为:
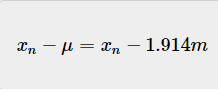
下表列出了每个变量与平均值的距离:

有些值为负值,为了去掉负值,让我们将计算距离的平方:
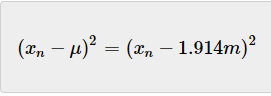
下表给出了每个变量与平均值的平方距离:

为了计算数据集的方差,我们需要计算所有平方距离的平均值:
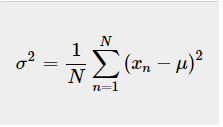
对于团队A,方差为:

对于团队B,方差为:

我们可以看到,虽然两支球队的平均值相同,但A队的身高分散程度高于B队的身高分散程度,A队球员与B对相比,类型更加丰富多样,有不同位置的球员,如控球手、中锋和后卫。
方差单位为平方米;查看标准偏差更方便,它是方差的平方根:
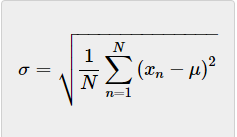
A队球员身高的标准偏差为0.12米。B队球员身高的标准偏差为0.036米。
现在,假设我们想计算所有高中篮球运动员的均值和方差,这将是一项艰巨的任务——我们需要收集每一所高中的每一位球员的数据。
然而,我们可以通过抽取一个比较大的样本并对该数据集进行计算来估计球员的均值和方差。
包含100个随机选择的球员数据的数据集应该足以进行准确的估计。
然而,当我们估计方差时,方差计算公式略有不同。我们将用因子N-1来归一化,而不是用因子N进行归一化:
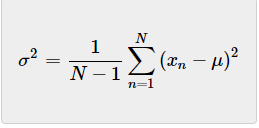
N−1称为贝塞尔修正。
你可以在visiondummy或维基百科上看到上述方程的数学证明。
- 相关推荐
- 热点推荐
- 卡曼滤波
-
卡曼滤波器入门教程概述2023-02-10 1170
-
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程2022-12-15 4466
-
卡尔曼滤波器是什么2021-11-16 1516
-
卡尔曼滤波器的使用原理2021-08-17 1443
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1154
-
卡尔曼滤波器原理2008-07-14 1296
全部0条评论

快来发表一下你的评论吧 !

