

卡曼滤波器入门教程数学基础2
模拟技术产品创意
描述
正态分布
事实证明,许多自然现象遵循正态分布,正态分布,也称为高斯分布(以数学家卡尔·弗里德里希·高斯命名),由以下等式描述:
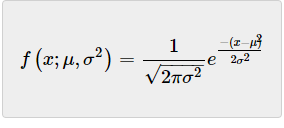
高斯曲线也被称为正态分布的概率密度函数(PDF)。
下图描述了三个城市的披萨配送时间PDF:城市A、城市B和城市C:
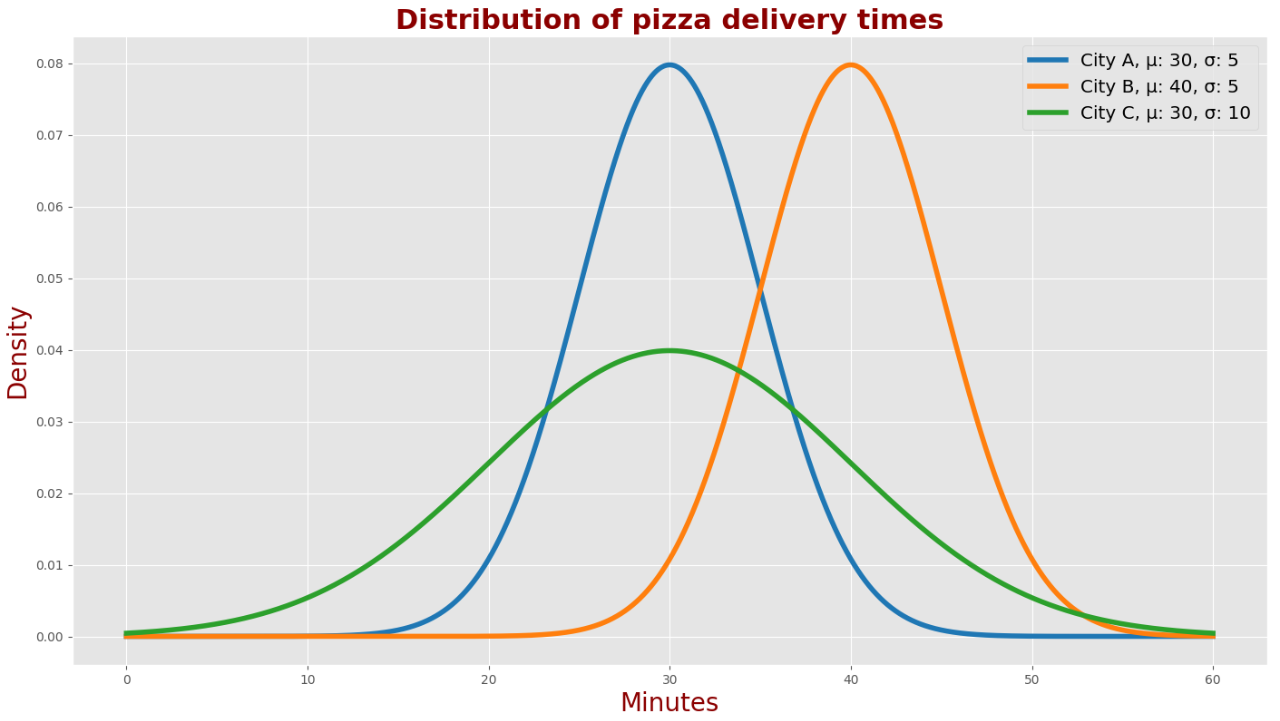
l在城市“A”,平均交货时间为30分钟,标准偏差为5分钟。l在城市“B”,平均交货时间为40分钟,标准偏差为5分钟。l在城市“C”,平均交货时间为30分钟,标准偏差为10分钟。
我们可以看到,城市“A”和城市“B”的披萨配送时间的高斯形状是相同的;然而,它们的中心是不同的,这意味着在A城市,你平均等待披萨的时间要少10分钟,而披萨配送时间的偏差程度是一样的。
我们还可以看到,城市“A”和城市“C”中的高斯曲线中心是相同的;然而,它们的形状不同。因此,这两个城市的平均披萨配送时间是相同的,但偏差程度不同。
下图描述了正态分布的比例:
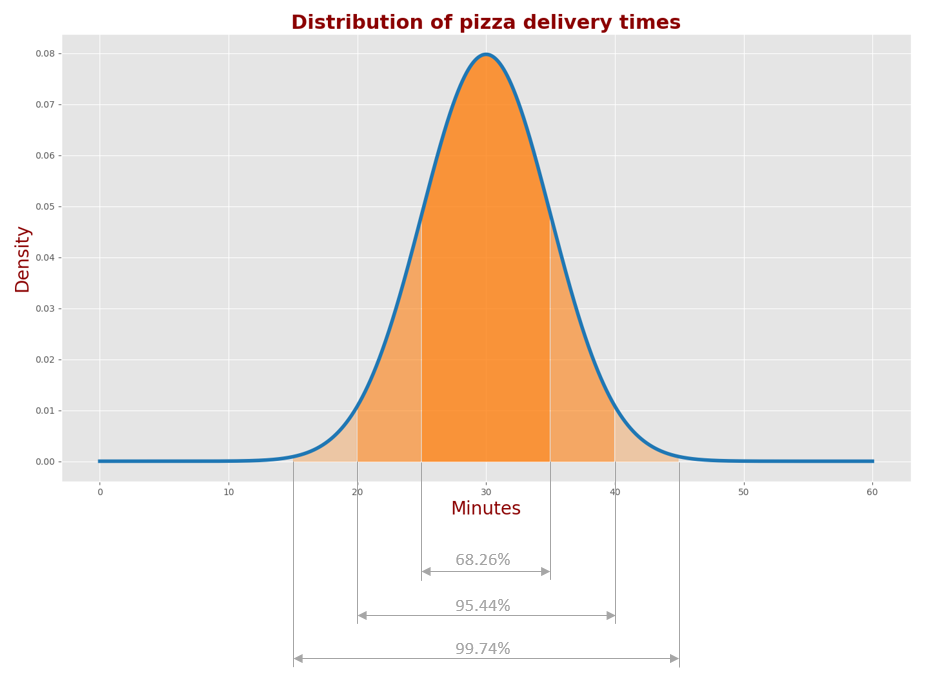
l68.26%的交货时间在μ±σ范围内(25-35分钟)l95.44%的交付时间在μ±2σ范围内(20-40分钟)l99.74%的交付时间在μ±3σ范围内(15-45分钟)
通常,测量误差是服从正态分布的,卡尔曼滤波器设计假设测量误差服从正态分布。
随机变量 `
随机变量描述系统的隐藏状态,随机变量是来自随机实验的一组可能值,随机变量可以是连续的或离散的:
l连续随机变量可以取特定范围内的任何值,例如电池充电时间或马拉松比赛时间是连续随机变量。l一个离散的随机变量是可计数的,例如网站访问者的数量或班级中的学生人数。
随机变量由概率密度函数描述,概率密度函数具有距的特性,随机值的矩是随机变量幂次方的期望值,我们对两种类型的矩感兴趣:
lK阶原点矩是随机变量k次幂的期望值:E(Xk)lK阶中心矩是随机变量分布关于其均值的第k次幂的期望值:E((X−μX)k)
在本教程中,随机变量的特征如下:
l一阶原点矩E(X)–测量序列的平均值l二阶中心力矩E((X−μX)2)–测量序列的方差
估计、准确度和精度
估计是对系统隐藏状态的评估,飞机的真实位置对观察者是隐藏的,我们可以使用雷达等传感器来估计飞机的位置,通过使用多个传感器并应用高级估计和跟踪算法(例如卡尔曼滤波器),可以显著改善估计,每个测量或计算的参数都是一个估计值。
准确度指示测量值与真实值的接近程度。
精度描述了同一参数的一系列测量的差异程度,准确度和精密度是估计的基础。
下图说明了精确度和精度:
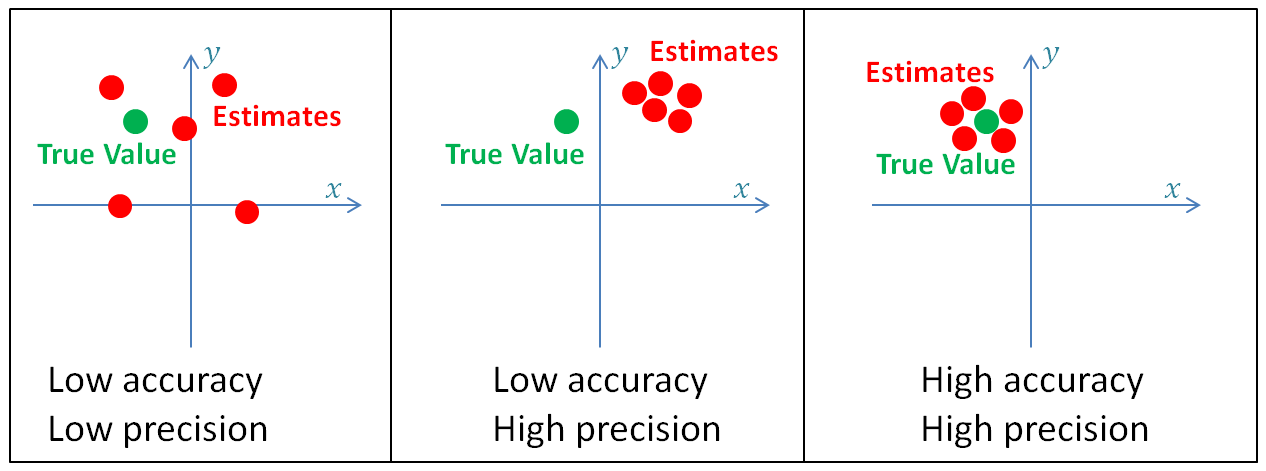
高精度系统的测量方差较小(即,不确定度较低),而低精度系统的度量方差较大(即,高不确定度),随机测量误差是方差产生的原因。
低准确度系统被称为有偏系统,因为它们的测量具有内置的系统误差(偏置)。
方差的影响可以通过平均或平滑测量来减小,例如,如果我们使用具有随机测量误差的温度计测量温度,我们可以进行多次测量并求平均值。由于误差是随机的,一些测量值将高于真实值,而其他测量值将低于真实值,估计值将接近真实值,我们做的测量越多,估计就越接近。
另一方面,有偏差的温度计会在估算中产生恒定的系统误差。
本教程中的所有示例都假定系统是无偏差的。
总结
下图显示了从统计学视的角度来看待测量:
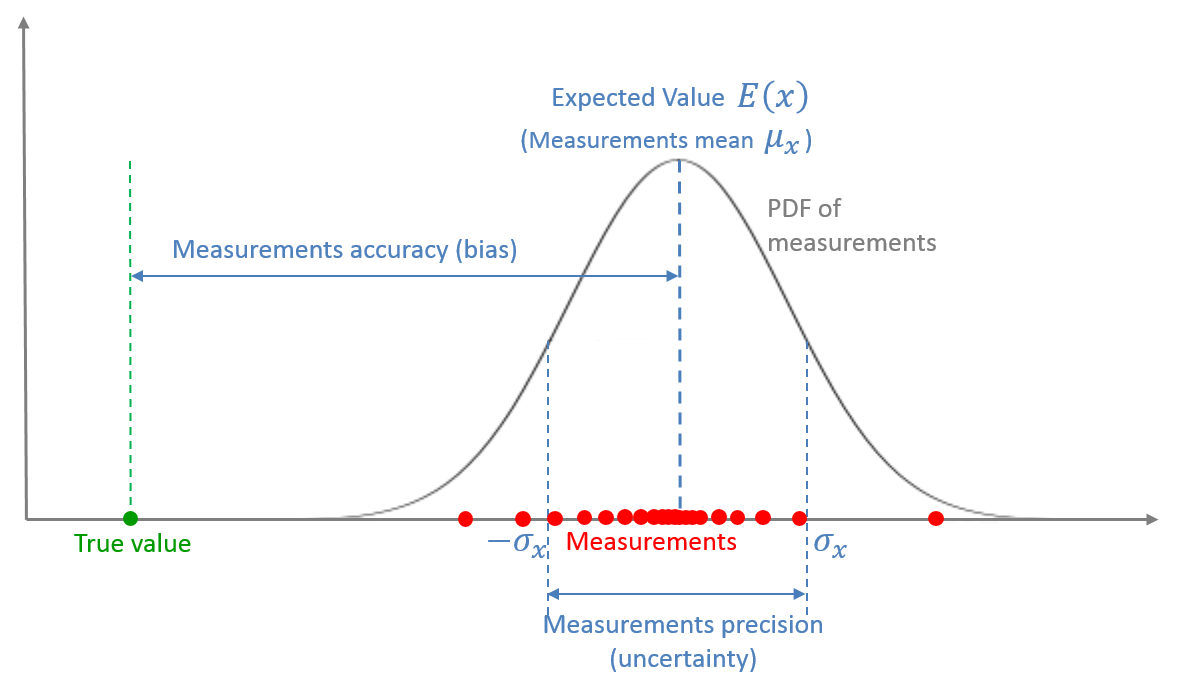
测量值是一个随机变量,由概率密度函数(PDF)描述。
测量的平均值是随机变量的期望值。
测量值的平均值和真实值之间的偏差是测量值的准确度,也称为偏差或系统测量误差。
测量值的离散度是测量精度,也称为测量噪声、随机测量误差或测量不确定度。
- 相关推荐
- 热点推荐
- 卡曼滤波
-
卡尔曼滤波的数学基础2023-08-30 1555
-
卡曼滤波器入门教程概述2023-02-10 1171
-
卡尔曼滤波器是什么2021-11-16 1516
-
卡尔曼滤波器的使用原理2021-08-17 1444
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1157
-
卡尔曼滤波器原理2008-07-14 1296
全部0条评论

快来发表一下你的评论吧 !

