卡曼滤波器入门教程α−β−γ滤波器 2

估计算法

下图描述了本示例中使用的估计算法：

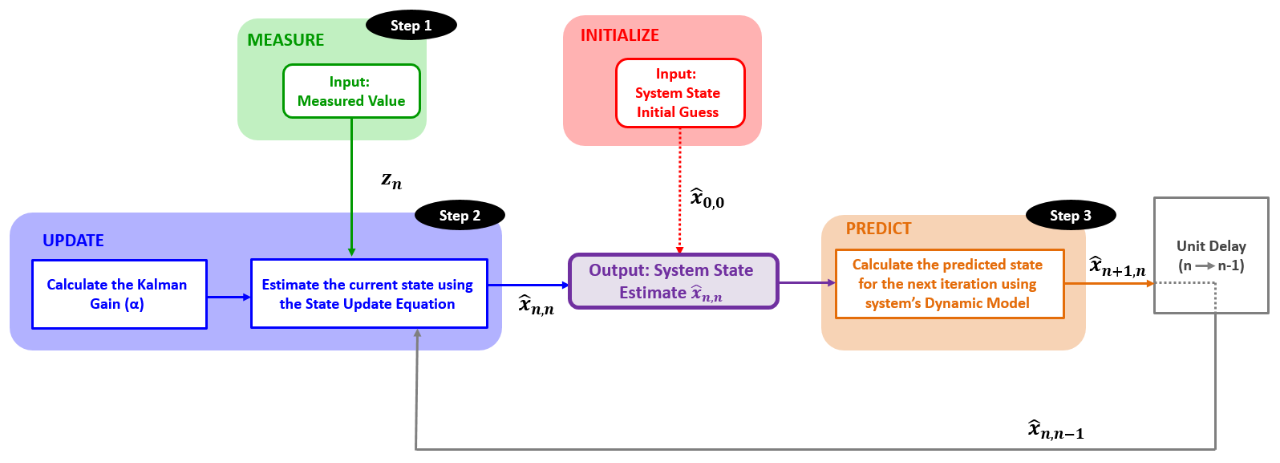
现在我们准备开始测量和估计过程。

迭代0：

初始化：

我们最初猜测金条的重量是1000克，初始猜测只进行一次且仅用于滤波器初始化阶段，因此，后续迭代过程中不需要它。

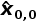
=1000g

预测：

金条的重量不应该改变，因此，系统的动态模型是静态的，我们的下一个状态估计（预测）等于初始化状态：

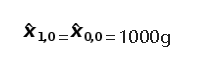
迭代1：

步骤1：

用天平秤对金条进行测量：

Z1=1030g

步骤2：

计算增益，在我们的示例中，αn=1/n，因此：

α1=1/1=1

使用状态更新方程计算当前估计：

=

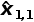
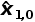
+α1(z1−

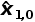
)=1000+1(1030−1000)=1030g

注意: 本示例中，初始估计值可以是任何值，因为α1=1，初始估计值会在第一轮迭代中被消除。

步骤3：

系统是静态的；因此，金条的重量不应该改变，我们的下一状态估计（预测）等于当前状态估计：

=

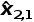
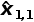
=1030g

迭代2：

在完成一个时间周期后，来自上一次迭代的预测估计变为当前迭代中的上一次估计：

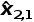
=1030g

步骤1：

进行第二次重量测量：

z2=989g

步骤2：

计算增益：

α2=1/2

计算当前估计：

=

+α2(z2−

)=1030+1/2(989−1030)=1009.5g

步骤3：

=

=1009.5g

迭代3：

z3=1017g α3=1/3

= 1009.5+13(1017−1009.5)=1012g

=1012g

迭代10：

z10=1011g α10=1/10

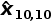
=1011+110(1011−1011)=1011gx^10,10=1011+110(1011−1011)=1011g

到这我们就可以停止了，增益随着每次测量而减小，因此，后续每次测量的贡献低于前一次测量的贡献，我们已经非常接近真实重量，即1010克。如果我们进行更多的测量，我们会更接近真实值。

下表对我们的测量值和估计值进行了总结，图表对测量值、估计值和真实值进行了比较。

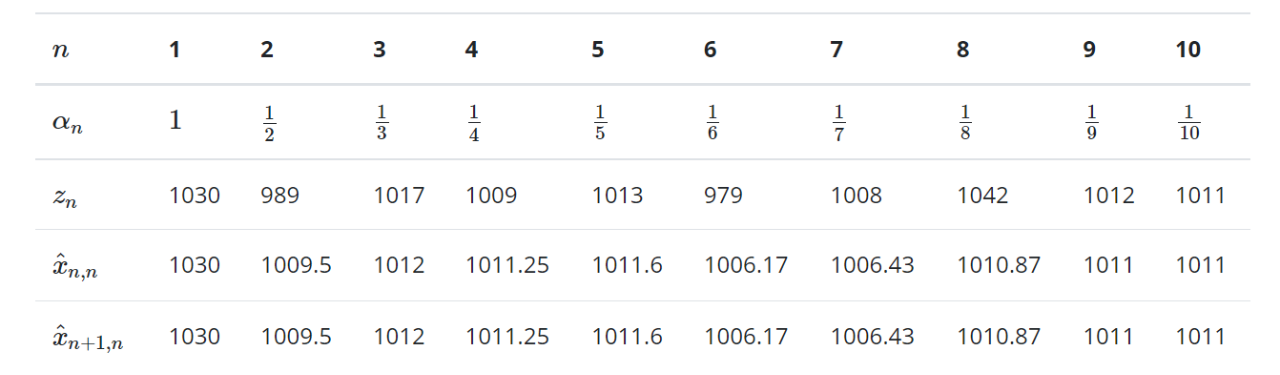
该估计算法对测量值具有平滑效果，并向真实值收敛。

在这个例子中，我们为静态系统开发了一个简单的状态估计算法，我们还导出了状态更新方程，这是五个卡尔曼滤波方程之一。

示例2：跟踪一维空间下的匀速飞行器

是时候研究一个随时间改变状态的动态系统了。在本例中，我们使用α-β滤波器跟踪匀速飞机的一维状态。

让我们假设一个一维世界，一架飞机正在径向远离雷达（或朝向雷达）移动，在一维世界中，雷达的角度是恒定的，飞机的高度也是恒定的。

xn表示时间n时飞机的航程，飞机速度可以使用航程微分法来近似，即测量航程随时间的变化。

因此，速度是航程的导数：

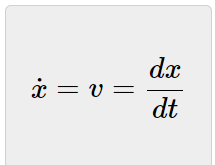
雷达以恒定速率向目标方向发送跟踪波束，时间间隔为Δt，下面两个运动方程可以描述系统匀速运动的动力学模型：

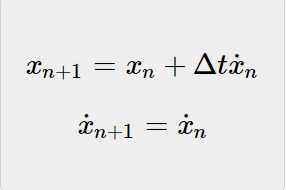
根据上面的方程，下一追踪周期的飞机航程等于当前追踪周期航程加上目标速度乘以追踪间隔，另外，由于我们在本例中假设速度恒定，因此，下一个周期的速度等于当前周期的速度。

上述方程组称为状态推导方程（也称为转换方程或预测方程），也是五个卡尔曼滤波方程之一，这个方程组将通过当前状态推导得到下一状态（预测）。

我们在上一个示例中也使用了状态推导方程，其中我们假设下一个周期的黄金重量等于当前周期的黄金重量。

状态推导方程取决于当前是什么系统，并因系统类型而异，状态推导方程可以使用矩阵进行表示，我们稍后再学习。

注意: 我们已经学习了五个卡曼滤波方程中的两个:状态更新方程状态推到方

现在，我们将修改本示例的状态更新方程。

α-β滤波器

让雷达进行跟踪（Δt周期为5秒），假设在时间n−1无人机的估计航程为30000m，估计无人机速度为40m/s。

使用状态推导方程，我们可以预测时间n时的目标位置：

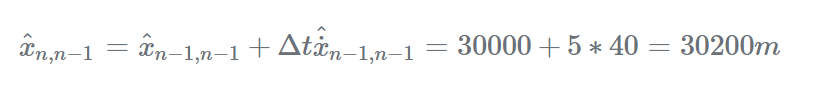
对于时间n的目标速度预测：

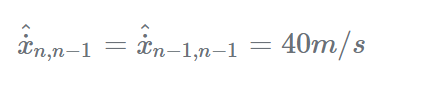
然而，在时间n，雷达测量的航程（zn）为30110米，而不是预期的30200米，预期（预测）值和测量值之间有90m的差距，造成这种差距的原因有两种：

l雷达测量不准确

l飞行器速度变了，新速度为：（30110-30200）/5 = 22m/s

上面哪一个假设是正确的？

让我们写下速度的状态更新方程：

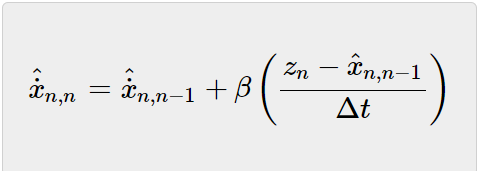
因子β的值取决于雷达的精度水平，假设雷达的1σ精度为20m，那么，预测距离和测量距离之间的90米差距很可能是飞机速度变化造成的，在这种情况下，我们应该将β因子设置为高值，如果我们设置β=0.9，则估计速度为：

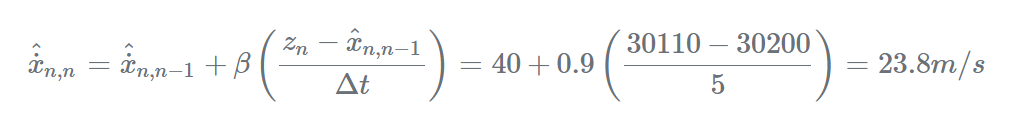
同理，假设雷达的1σ精度为150米，那么90米的距离偏差可能是雷达测量误差造成的。在这种情况下，我们应该将β因子设置为较低的值，如果我们设置β=0.1，则估计速度为：

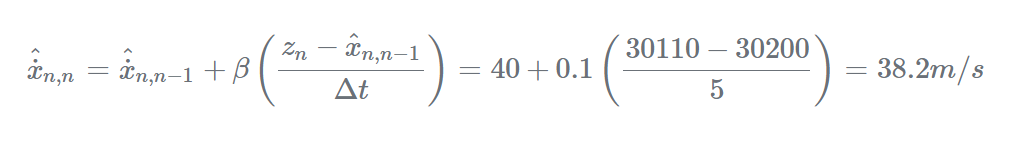
如果飞机速度真的从40m/s变为22m/s，我们可以在10个追踪周期后发现它（以β=0.1运行上述等式10次）。如果差距是由测量误差引起的，则后续的测量值将在真实值上下轻微浮动，因此，平均而言，目标速度不会改变。

飞机位置的状态更新方程类似于前一示例中导出的方程：

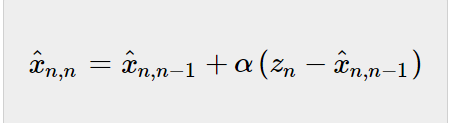
与前面的例子不同，在每次迭代中都会重新计算α因子（αn=1/N），在本例中α因子是常数。

α因子的大小取决于雷达测量精度。对于高精度雷达，我们应该选择高α，给测量值赋予高权重，如果α=1，则估计值将等于测量值：

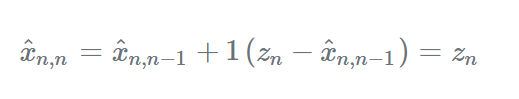
如果α=0，则测量值没有意义：

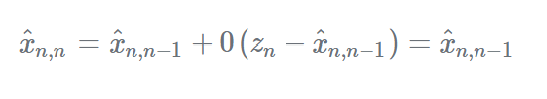
因此，我们推导出了一个方程组，它构成了雷达跟踪器的状态更新方程，它们也被称为α−β轨迹更新方程或α−β轨迹滤波方程。

注意: 在某些书籍中, α−β滤波器也被叫做g-h滤波器

注意: 在本例中，我们从航程测量值得出飞机速度，现代雷达可以利用多普勒效应直接测量径向速度，然而，我的目标是解释卡尔曼滤波器，而不是雷达操作。因此，为了通用性，我将继续从我们的示例中的距离测量中推导出速度。

下图描述了本示例中使用的估计算法：

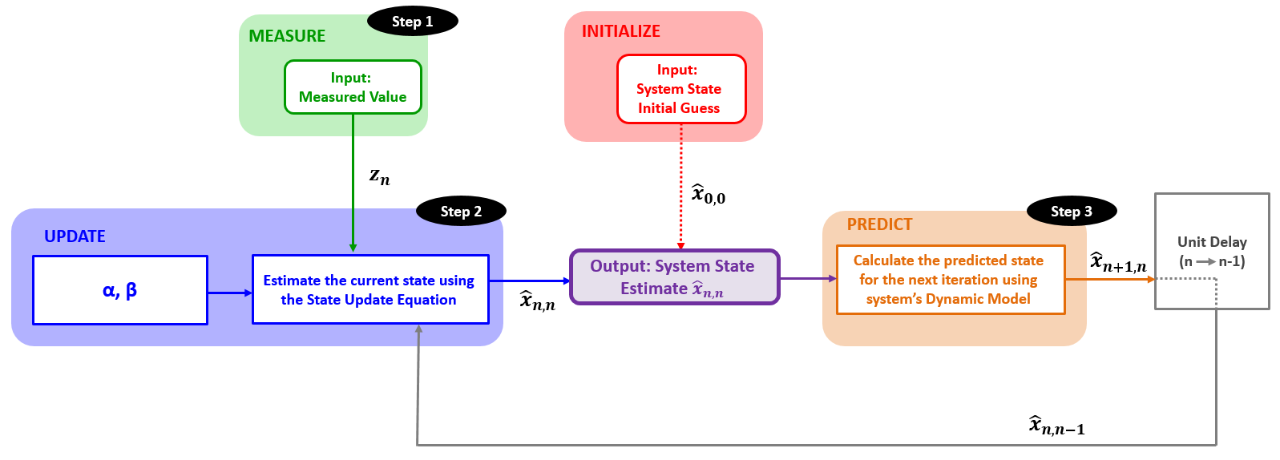
与前一示例不同，本示使用了增益值α和β，在卡尔曼滤波器中，α和β被卡尔曼增益代替，卡尔曼增益是在每次迭代时计算得到的，我们稍后才了解。