

卡曼滤波器入门教程α−β−γ滤波器 4
模拟技术
描述
示例4:使用用α−β−γ滤波器追踪加速飞行器
在这个例子中,我们使用α−β−γ过滤器跟踪一架恒定加速度的飞行器。
α−β−γ滤波器
α−β−γ滤波器(有时称为g-h-k滤波器)考虑目标加速度。因此,状态外推方程变为:

状态更新方程变为:
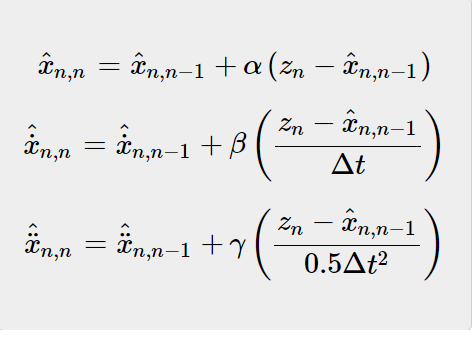
数值示例:
让我们以上一个例子中的场景为例:一架飞机以50m/s的恒定速度移动15秒,然后以8m/s2的恒定加速度加速35秒。
α-β-γ滤波器参数为:
α=0.5
β=0.4
γ=0.1
追踪周期为5秒
迭代0:
初始化:
给出了时间n=0的初始条件:
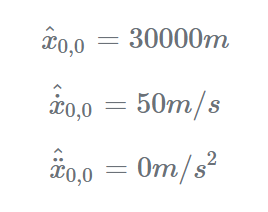
预测:
应使用状态推导方程外推得到第一个周期(n=1)状态:
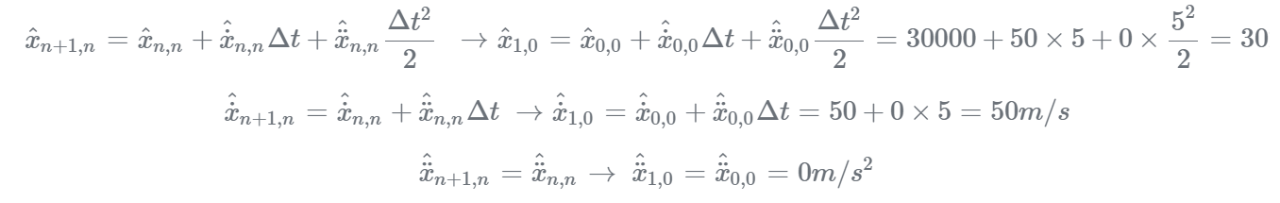
迭代1:
在第一个周期(n=1)中,初始猜测是先前的估计:
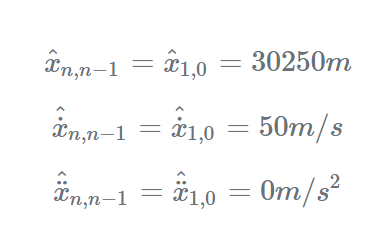
步骤1:
雷达测量飞机航程:
z1=30160m
步骤2:
使用状态更新方程计算当前估计:
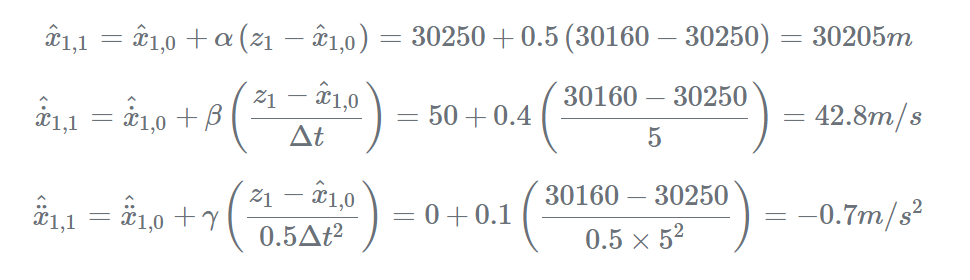
步骤3:
使用状态推导方程计算下一状态估计:
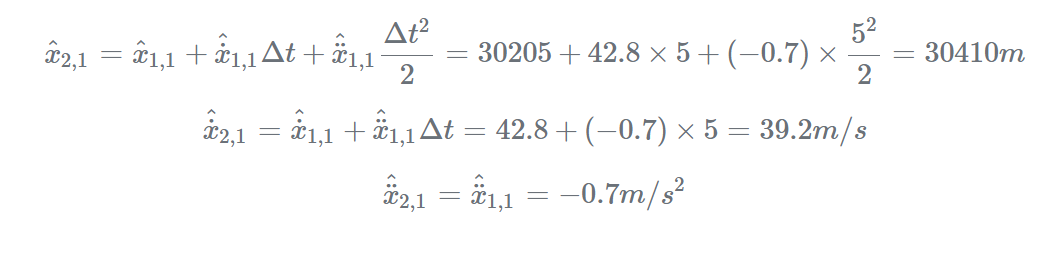
迭代2:
经过一个完整周期后,来自前一个迭代的预测估计变为当前迭代中的先前估计。
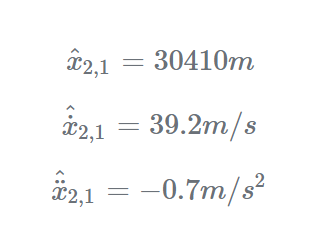
步骤1:
雷达测量飞机航程:
z2=30365m
步骤2:
使用状态更新方程计算当前估计:
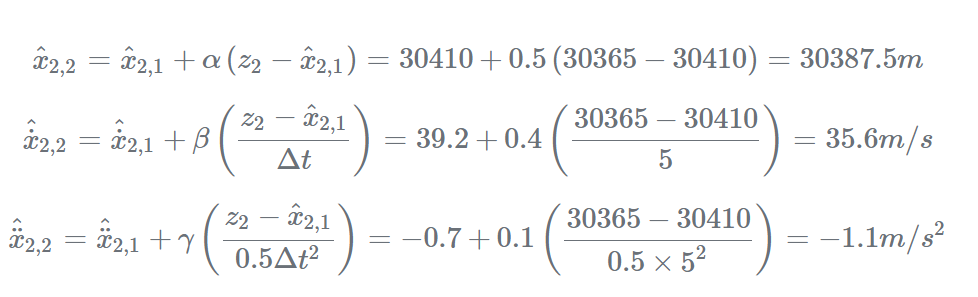
步骤3:
使用状态推导方程计算下一状态估计:
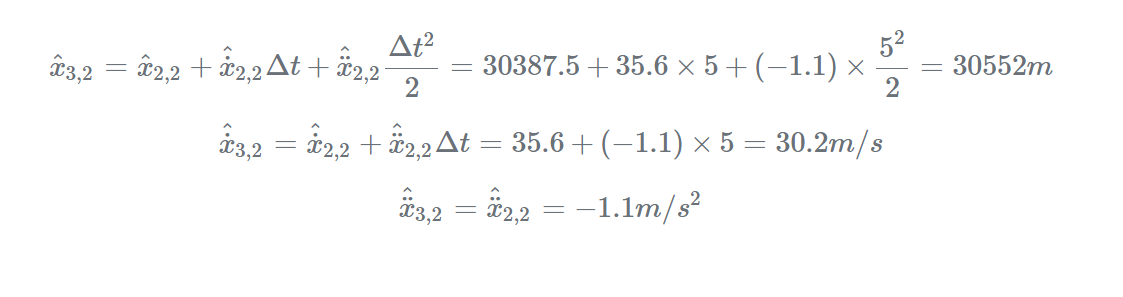
迭代3-10:
下表总结了连续迭代的计算:


以下图表比较了前50秒的距离、速度和加速度的真实值、测量值和估计值:
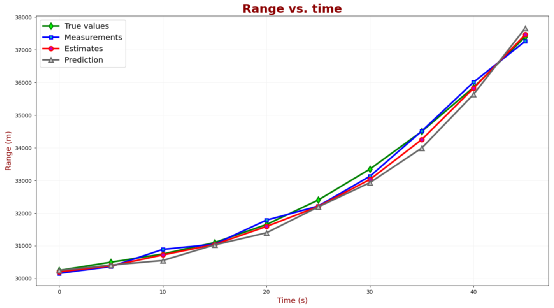
如你所见,包含加速度的动态模型方程的α−β−γ滤波器可以在恒定加速度下跟踪目标并消除滞后误差。
但是在机动目标的情况下会发生什么?目标可以通过机动突然改变飞行方向,目标的动态模型还可以包括急动(改变加速度),在这种情况下,带有恒定滤波器系数得α−β−γ滤波器会产生估计误差,在某些情况下会丢失目标轨迹。
卡尔曼滤波器可以处理动态模型中的不确定性,这是我们的下一个主题,就在总结之后。
总结:
存在有多种类型α−β−γ滤波器,它们基于相同的原理:
l当前状态估计基于状态更新方程。
l下一个状态估计(预测)基于动态模型方程。
这些滤波器之间的主要区别在于权重系数α−β−γ的选择,一些滤波器类型使用恒定的权重系数;其他的通过计算得到每个滤波器迭代的权重系数。
α、β和γ的选择对于估计算法的正确运行至关重要。
α−β−γ应该是什么参数?作为卡尔曼滤波器的介绍,我这里只做简单介绍,因此,我不讨论这个主题。好奇的读者可以找到许多关于这个主题的书籍和论文。作为参考,我建议:
Dirk Tenne, Tarunraj Singh. “Optimal Design of α−β−(γ)α−β−(γ) Filters”. State University of New York at Buffalo.
-
卡尔曼滤波是属于一个什么滤波器?2023-10-11 649
-
卡曼滤波器入门教程概述2023-02-10 1161
-
卡尔曼滤波器是什么2021-11-16 1508
-
卡尔曼滤波器的使用原理2021-08-17 1427
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1136
-
图解卡尔曼滤波器2018-02-07 5047
-
卡尔曼滤波器参数分析与应用方法研究2016-06-21 863
-
卡尔曼滤波器原理2008-07-14 1293
全部0条评论

快来发表一下你的评论吧 !

