

卡曼滤波器入门教程一维卡曼滤波器 2
电子说
描述
示例5–估计建筑物的高度
假设我们要用非常不精确的高度测量仪来估计建筑物的高度,我们知道,建筑高度不会随时间变化,至少在短期测量过程中是如此。
数值示例
建筑真实高度是50米。高度测量仪测量误差(标准偏差)为5米。十个测量值分别为:48.54m、47.11m、55.01m、55.15m、49.89m、40.85m、46.72m、50.05m、51.27m、49.95m。迭代0初始化可以通过简单的观察来估计建筑物的高度,预计建筑高度为:
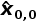
=60m
现在我们将初始化估计不确定度,一个人的估计误差(标准差)约为15米:σ=15,因此,方差为225:σ2=225。
p0,0=225
预测现在,我们将根据初始化值预测下一个状态:由于我们系统是恒定的,即建筑物不会改变其高度:
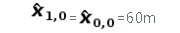
推导出来的估计不确定性(方差)也没有变化:
p1,0=p0,0=225
迭代1步骤1-测量第一次测量为:z1=48.54m由于高度计测量误差的标准偏差(σ)为5,方差(σ2)为25,因此测量不确定度为:r1=25。步骤2-更新计算卡尔曼增益:
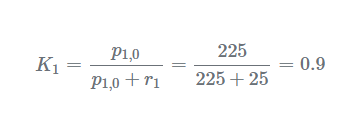
估计当前状态:
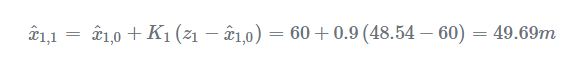
更新当前估计的不确定度:
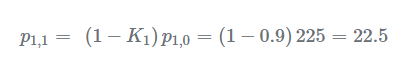
步骤3-预测由于我们系统是恒定的,即建筑物不会改变其高度:
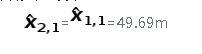
推导估计不确定度(方差)也没有变化:
p2,1=p1,1=22.5
迭代2经过一个迭代后,来自上一次迭代的预测估计变为当前迭代中的上一次估计:
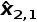
=49.69m
推导的估计不确定度变为先前的估计不确定度:
p2,1=22.5
步骤1-测量第二次测量为:z2=47.11m测量不确定度为:r2=25步骤2-更新计算卡尔曼增益:
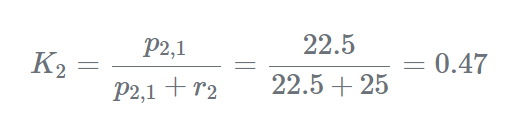
估计当前状态:
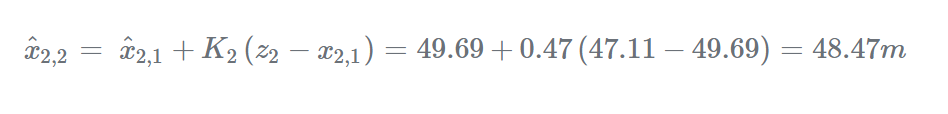
更新当前估计的不确定度:
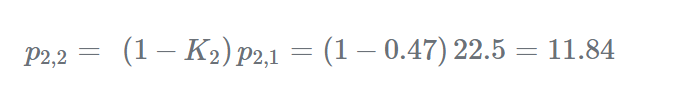
步骤3-预测由于我们系统是恒定的,即建筑物不会改变其高度:
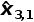
=
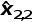
=48.47m
推导估计不确定度(方差)也没有变化:
p3,2=p2,2=11.84
迭代3-10下表总结了后续迭代的计算:
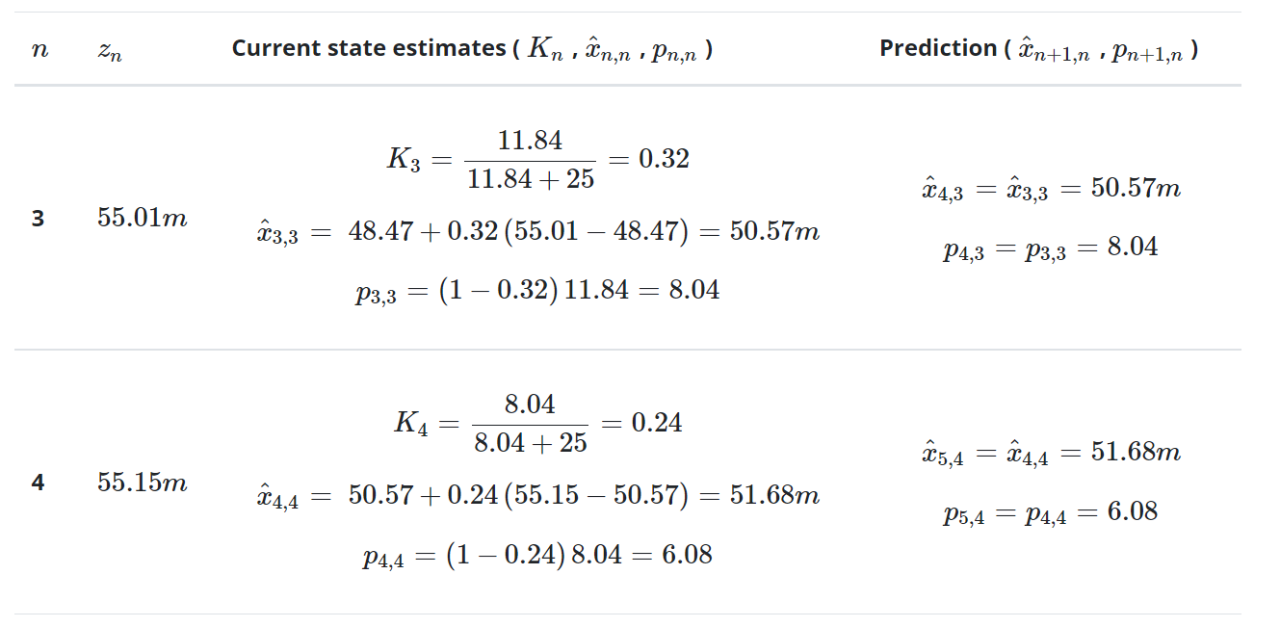
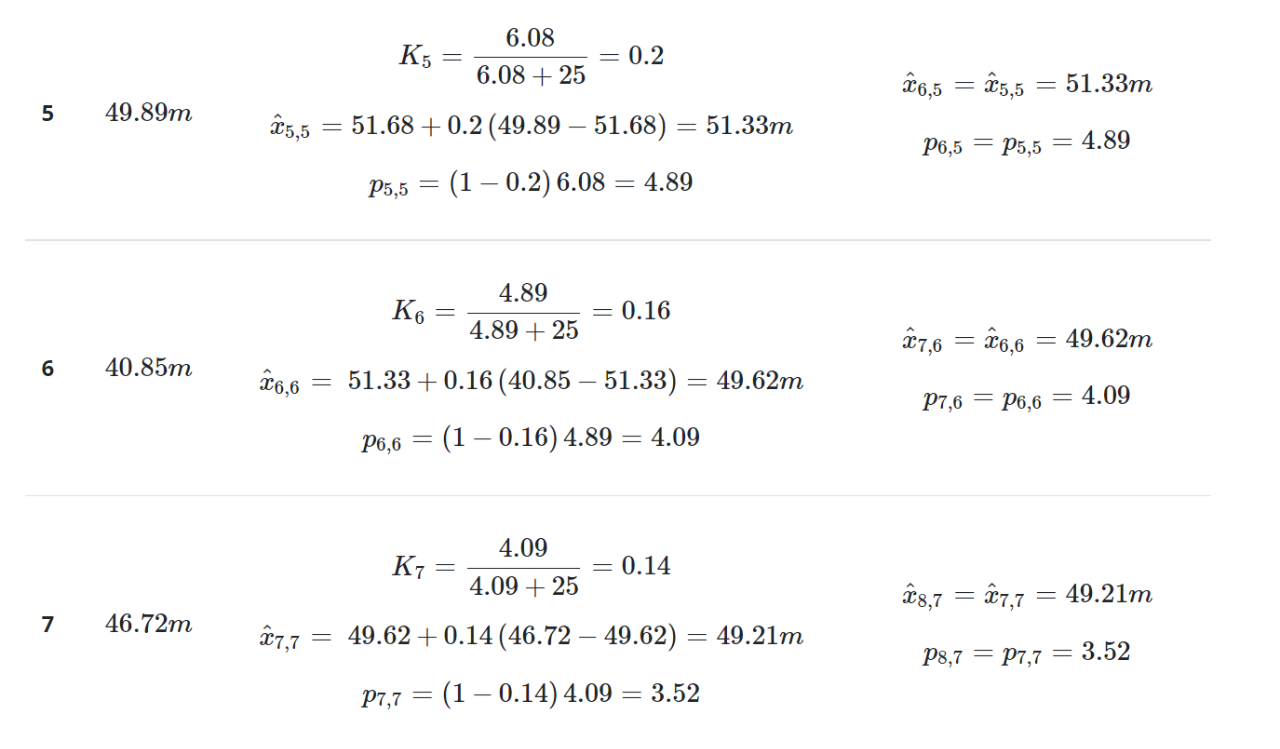
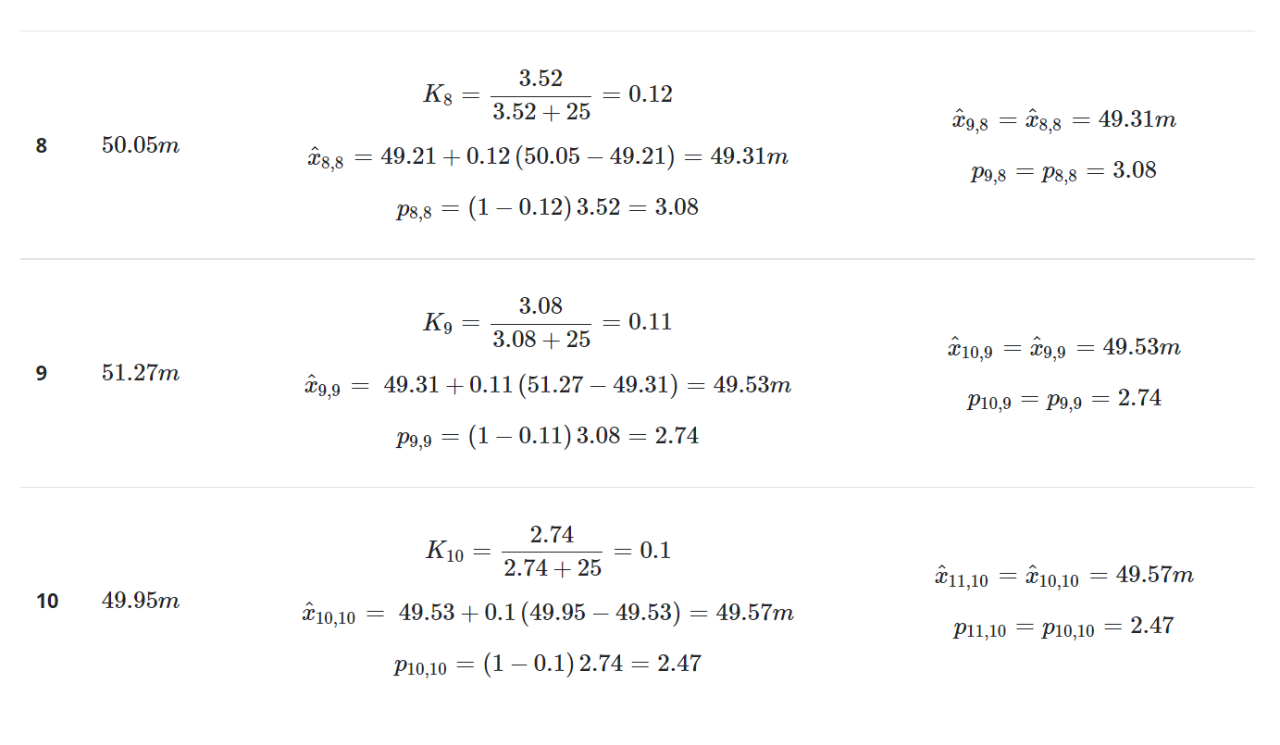
下表对真实值、测量值和估计值进行了比较:
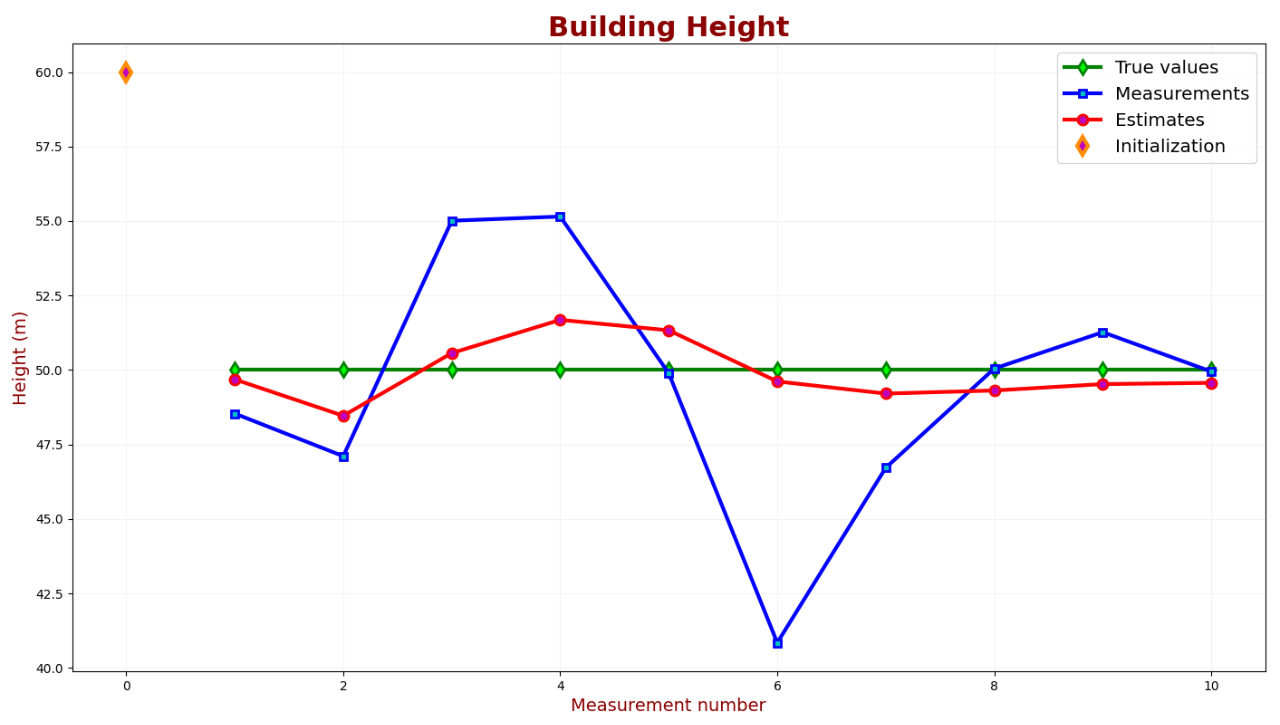
如图可见,经过7次测量,估计值收敛到约49.5米。下表对测量不确定度和估计不确定度进行了比较:
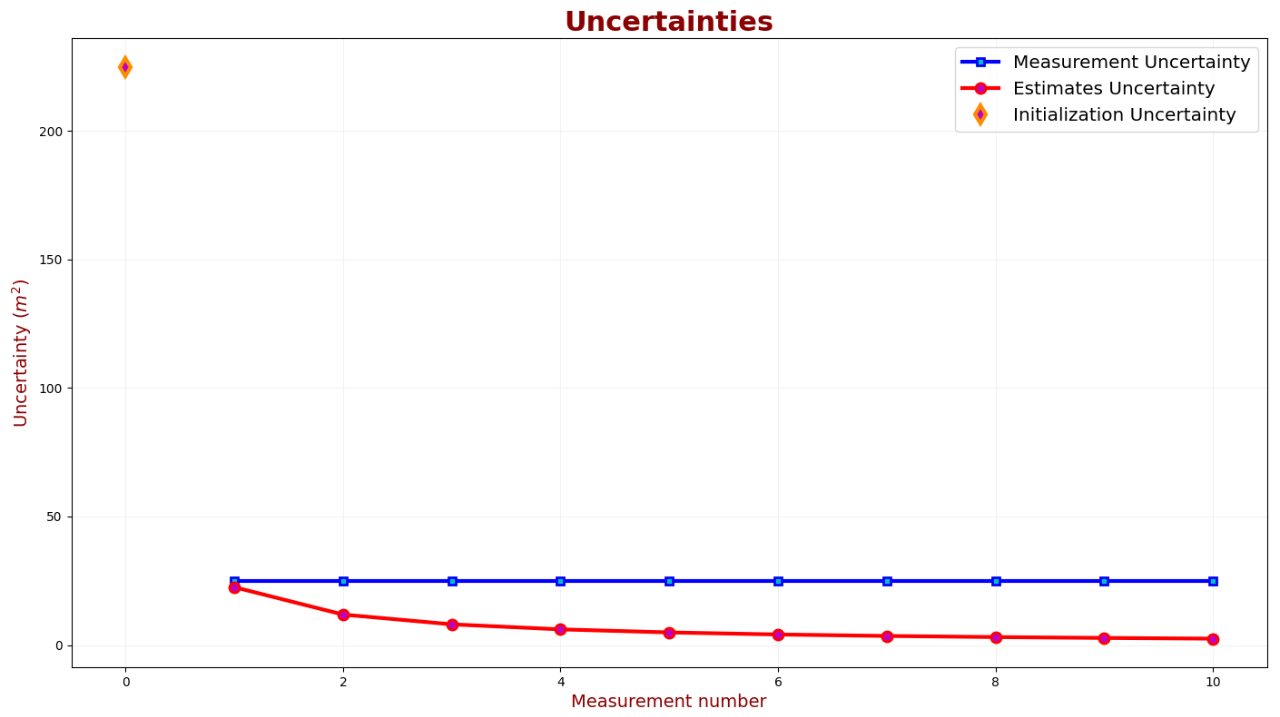
在滤波器第一轮迭代时,估计不确定度接近测量不确定度,并迅速降低,10次测量后,估计不确定度(σ2)为2.47,即估计误差标准偏差为:σ=1.57米。因此,我们可以说建筑高度估计为:49.57±1.57m。下图显示了卡尔曼增益:
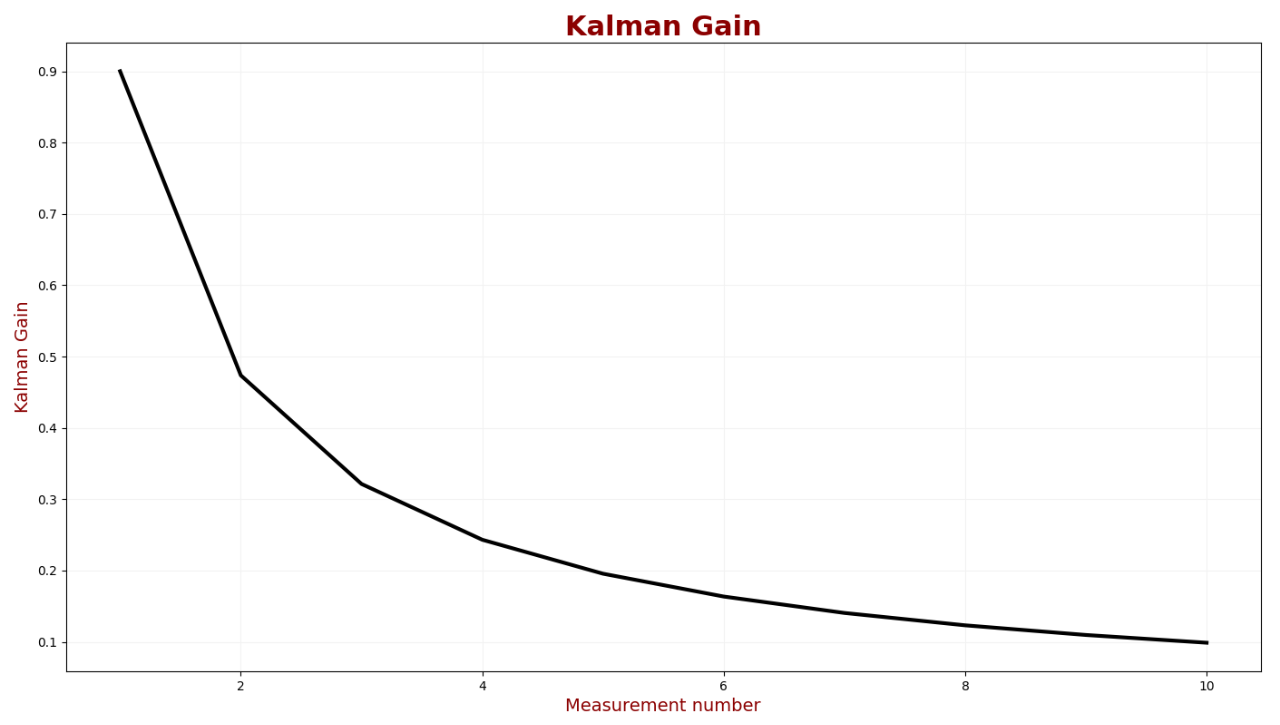
如图所见,卡尔曼增益正在逐渐减小,使测量权重越来越小。
总结:
在本例中,我们使用一维卡尔曼滤波器测量了建筑物高度,与α−β−γ不同,本示例中的卡曼增益是动态的,取决于测量设备的精度。卡尔曼滤波器使用的初始值不是很精确,因此,状态更新方程中的测量权重比较高,估计不确定度也很高,在后续每次迭代中,测量权重较低;因此,估计的不确定度也较低。卡尔曼滤波器输出包括估计和估计不确定度。
一维卡尔曼滤波器的完整模型
为了使得一维卡尔曼滤波器模型更加完整,我们需要在协方差推导方程中添加过程噪声变量。
过程噪声:
在现实世界中,动态系统模型存在不确定性,例如,当我们想要估计电阻器的电阻值时,我们假设一个恒定的动态模型,即电阻在测量之间不改变。然而,由于环境温度的波动,电阻可能略有变化,当用雷达跟踪弹道导弹时,动态模型的不确定性包括目标加速度的随机变化,由于可能的飞机机动,不确定性对飞机来说更为重要。相反,当我们使用GPS接收机估计静态对象的位置时,由于静态对象不移动,动态模型的不确定性为零;动态模型的不确定性称为过程噪声,在文献中,它也被称为对象干扰、驱动噪声、动力学噪声、模型噪声和系统噪声。过程噪声产生估计误差。在前面的示例中,我们估计了建筑物的高度。由于建筑物的高度没有变化,我们没有考虑过程噪声。过程噪声方差用字母q表示。协方差推导方程应包括过程噪声。对于恒定动态系统模型的协方差推导方程为:
pn+1,n=pn,n+qn
以下是更新后的一维卡尔曼滤波方程:
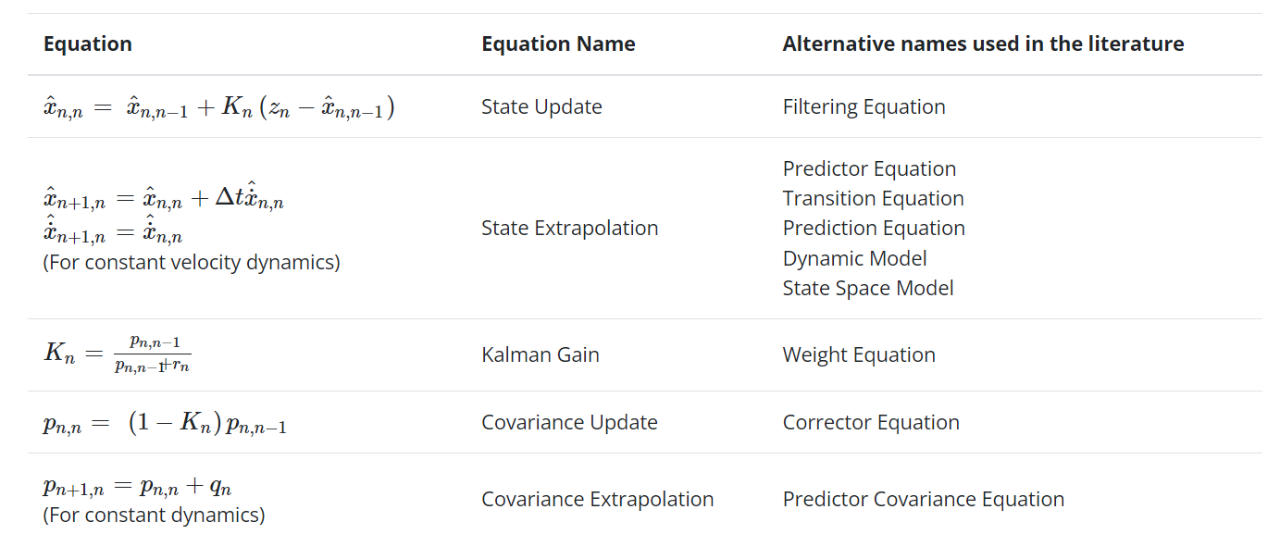
注意1:状态推导方程和协方差推导方程取决于系统类型。注意2: 上表展示了针对特定情况定制的卡尔曼滤波器方程的特殊形式,方程的一般形式将在后面的矩阵表示法中给出,现在,我们的目标是理解卡尔曼滤波器的概念。
- 相关推荐
- 热点推荐
- 卡尔曼滤波器
-
卡尔曼滤波是属于一个什么滤波器?2023-10-11 652
-
卡曼滤波器入门教程概述2023-02-10 1162
-
卡尔曼滤波器是什么2021-11-16 1511
-
卡尔曼滤波器的使用原理2021-08-17 1432
-
基于卡尔曼滤波器的PID设计教程2021-06-03 1143
-
图解卡尔曼滤波器2018-02-07 5050
-
卡尔曼滤波器参数分析与应用方法研究2016-06-21 863
-
卡尔曼滤波器原理2008-07-14 1293
全部0条评论

快来发表一下你的评论吧 !

