卡曼滤波器入门教程一维卡曼滤波器 3

示例6–估计储罐中液体的温度

我们想估计储罐中液体的温度：

我们假设在稳定状态下，液体温度是恒定的，然而，真实液体温度是存在一些波动的，我们可以用以下方程描述该动态系统状态：

xn=T+wn

T是恒定温度wn是具有方差q的随机过程噪声

数值示例：

假设真实温度为50摄氏度我们假设模型是准确的，因此，我们将过程噪声方差（q）设置为0.0001测量误差（标准偏差）为0.1摄氏度。每5秒测量一次。每个测量点对应的真实液体温度值为：49.979℃、50.025℃、50℃、50.003℃、49.994℃、50.002℃、4.9.999℃、50.006℃、49.998℃和49.991℃。测量值为：49.95℃、49.967℃、50.1℃、50.106℃、49992℃、49.819℃、49933℃、50.007℃、50.023℃和49.99℃。下表对真实液体温度和测量值进行了比较：

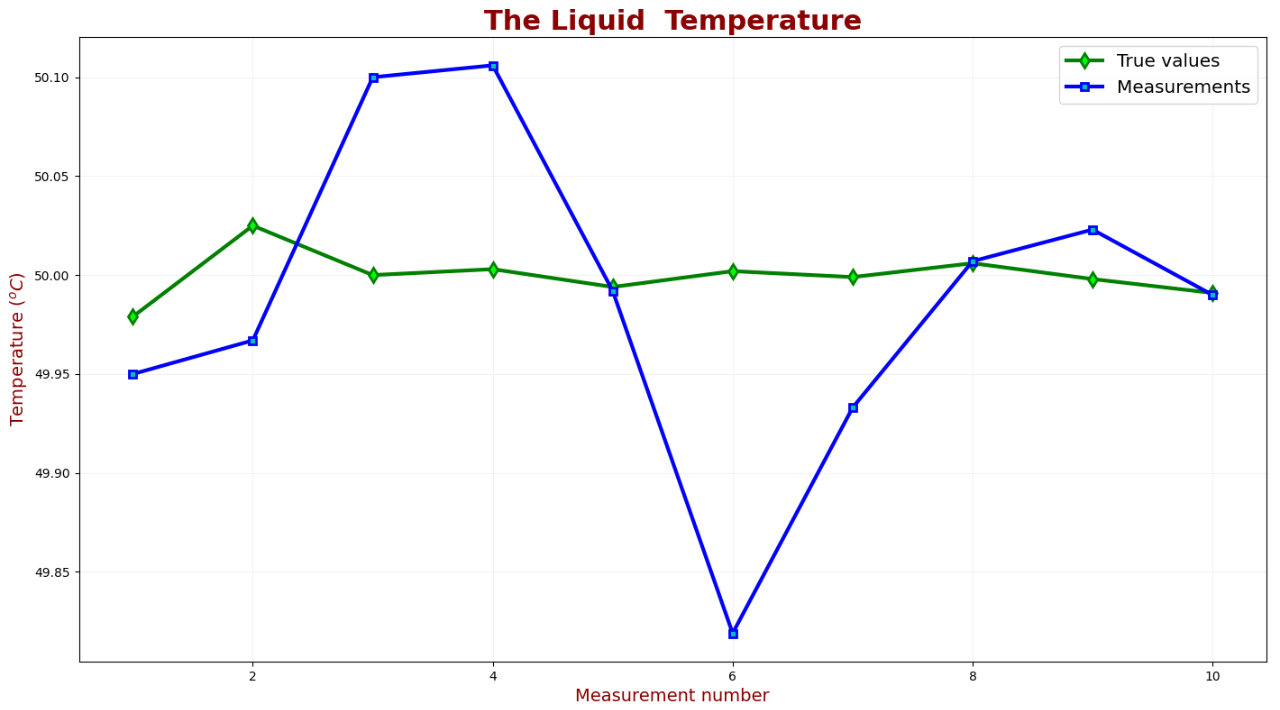
迭代0

在第一次迭代之前，我们必须初始化卡尔曼滤波器并预测下一个状态（即第一个状态）。

初始化

我们不知道储罐中液体的真实温度，我们的猜测是10℃

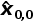
=10

℃我们的猜测很不精确，因此我们将初始化估计误差σ设置为100，初始化的估计不确定度是误差方差（σ2）：

p0,0=1002=10,000

方差非常大，如果我们用一个更有意义的初始化值，我们能够让卡尔曼滤波器更快地收敛。

预测

现在，我们将根据初始化值预测下一个状态，由于我们的模型是恒定的，预测的估计值等于当前的估计值：

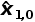
=10

℃推导估计不确定度（方差）：

p1,0=p0,0+q=10000+0.0001=10000.0001

迭代1步骤1-测量测量值是：

z1= 49.95

℃由于测量误差为0.1（σ），方差（σ2）为0.01；因此，测量不确定度为：

r1=0.01

步骤2-更新

计算卡曼增益：

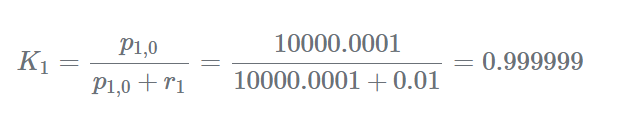
卡尔曼增益几乎为1，即我们的估计误差远大于测量误差，因此，估计的权重可以忽略不计，而测量权重几乎为1。估计当前状态：

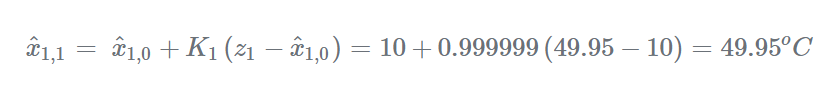
更新当前估计的不确定度：

步骤3-预测

由于我们系统是恒定的，即液体温度不变：

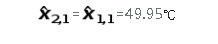
℃推导估计不确定值（方差）为：

p2,1=p1,1+q=0.01+0.0001=0.0101

迭代2步骤1-测量

测量值：

z2= 49.967

℃由于测量误差为0.1（σ），方差（σ2）为0.01；因此，测量不确定度为：

r2=0.01

步骤2-更新

计算卡曼增益：

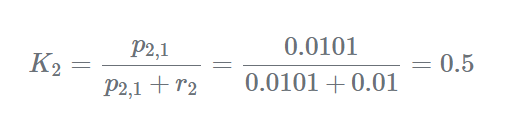
卡尔曼增益为0.5，即，估计权重和测量权重相等。估计当前状态：

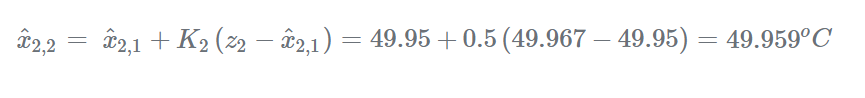
更新当前估计的不确定性：

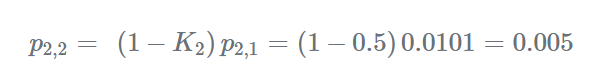
步骤3-预测

由于我们系统是恒定的，即液体温度不变：

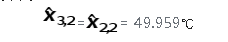
℃推导估计不确定度（方差）为：

P3,3=p2,2+q= 0.005+0.0001=0.0051

迭代3-10

下表总结了连续迭代的计算：

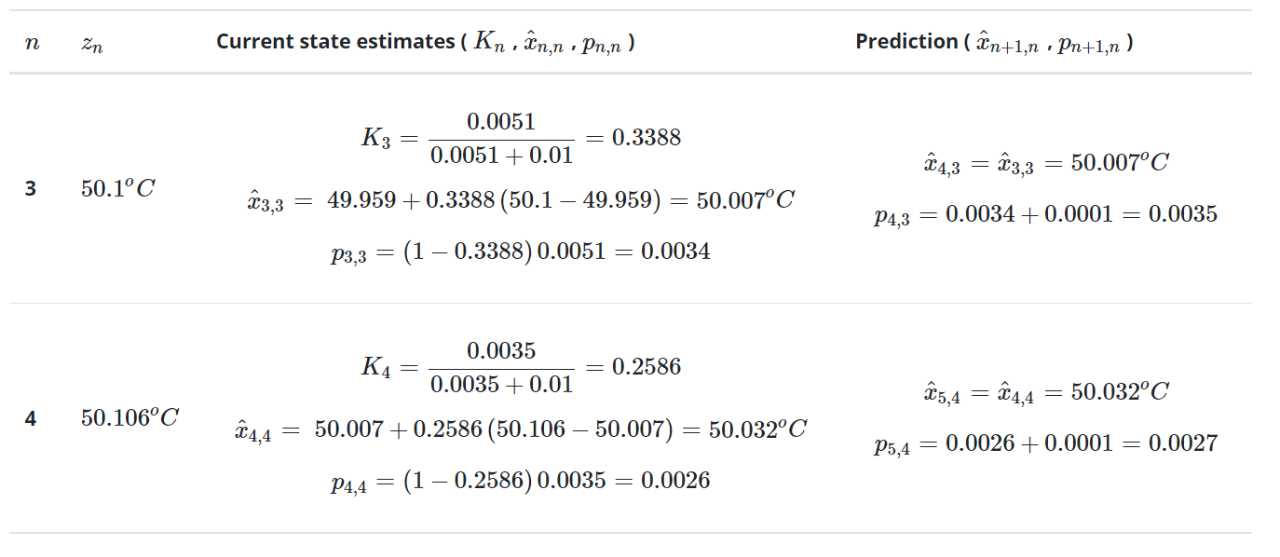
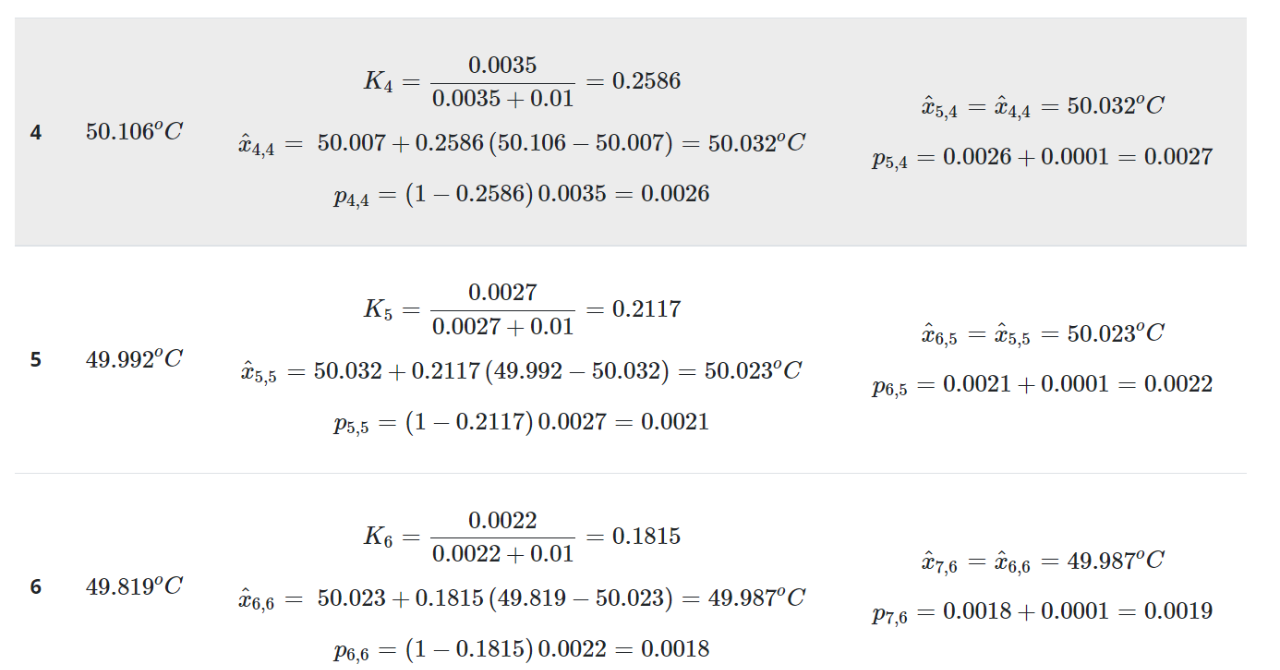
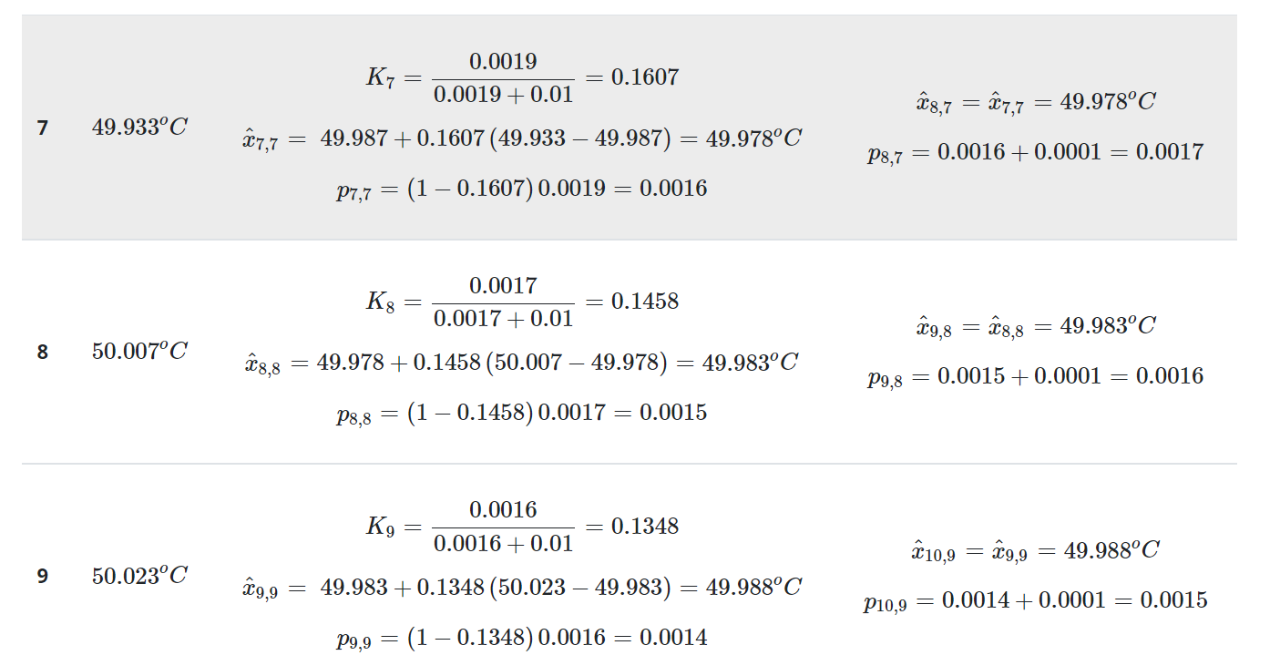
下表对真实值、测量值和估计值进行了比较：

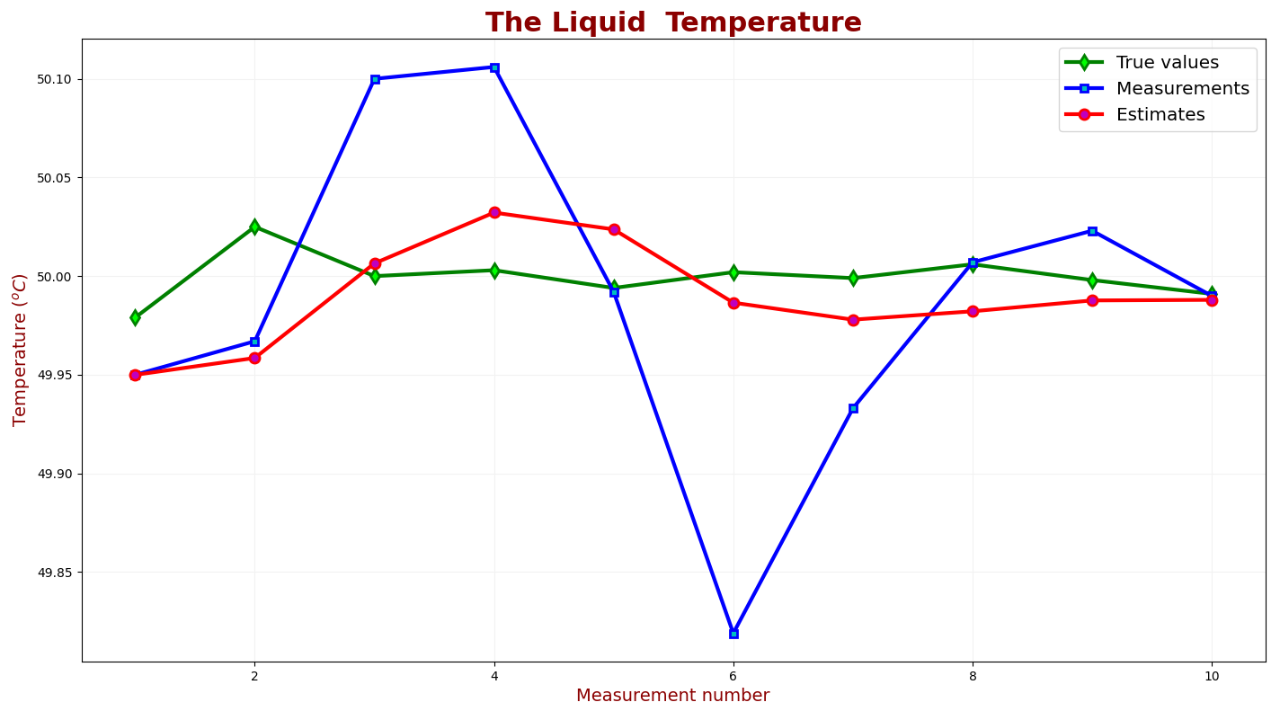
如图所见，估计值向真实值收敛，下表显示了估计的不确定性：

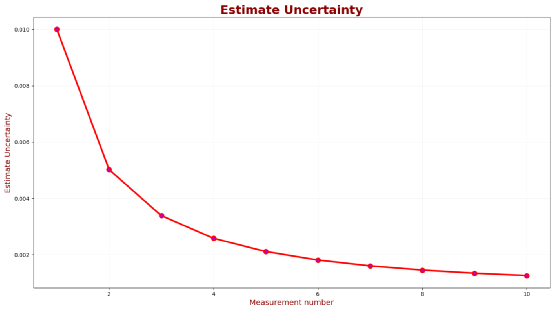
估计的不确定度迅速下降，10次测量后，估计不确定度（σ2）为0.0013，即估计误差标准偏差为：σ=0.036℃。因此，我们可以说液体温度估计值为：49.988±0.036℃

正如你所看到的，卡尔曼增益正在逐步下降，使得测量重量越来越小。

总结：

在本例中，我们使用一维卡尔曼滤波器测量液体温度，尽管系统包括随机过程噪声，但卡尔曼滤波器可以提供良好的估计。