大学课程 数据分析 实战之主成分分析（1）

本系列文章会先简单介绍主成分分析（PCA）的基本原理，然后用实例介绍分析的过程以及算法代码。PCA主要用于数据降维。由一系列特征组成的多维向量，其中某些元素本身没有区分性，比如某个元素在所有的样本中都相等，或者彼此差距不大，那么这个元素本身就没有区分性，如果用它做特征来区分，贡献会非常小。我们的目的是找到那些变化大的元素，即方差大的维，而去除掉那些变化不大的维。使用PCA的好处在于可以对新求出的“主元”向量的重要性进行排序。根据需要取前面最重要的部分，将后面的维数省去，从而达到降维、简化模型或对数据进行压缩的效果。同时最大程度地保持了原有数据的信息，较低的维数意味着运算量的减少，在数据较多的情况带来的性能提高更明显。

PCA通过将主成分分析的问题转化为求解协方差矩阵的特征值和特征向量来计算。其目标是寻找r（r小于原先的个数n）个新变量，使它们反映事物的主要特征，压缩原有数据矩阵的规模，每个新变量是原有变量的线性组合，体现原有变量的综合效果，这r个新变量称为“主成分”，它们可以在很大程度上反映原来n个变量的影响，并且这些新变量是互不相关的，也是正交的。主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法，从数学角度来看，这是一种降维处理技术。可以使用自带函数来完成，也可以使用自编函数来实现！这些内容都在本文中得到体现！

PCA自带函数！！！

MATLAB 2021a版本里面有主成分分析的函数pca。先看语法，然后在程序中使用看看效果！预先提示：计算相关系数的方式有些特别，居然用到了SVD算法，新奇！

由于主成分分析（principile component analysis，PCA）这个概念在不同领域（统计学、数学等）的解释差异较大，所以，本文通过示例使用对该函数做一点儿解释。

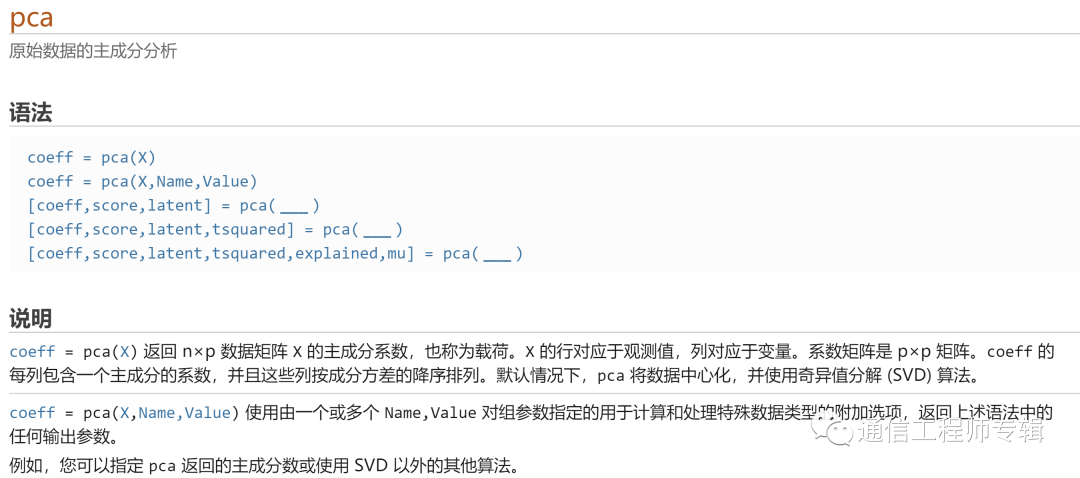
语法：

coeff = pca(X)

coeff = pca(X,Name,Value)

[coeff,score,latent] = pca(___)

[coeff,score,latent,tsquared] = pca(___)

[coeff,score,latent,tsquared,explained,mu] = pca(___)

[coeff,score,latent] = pca(___) 还在 score 中返回主成分分数，在 latent 中返回主成分方差。您可以使用上述语法中的任何输入参数。主成分分数是 X 在主成分空间中的表示。score 的行对应于观测值，列对应于成分。主成分方差是 X 的协方差矩阵的特征值。

原文标题：大学课程 数据分析 实战之主成分分析（1）

文章出处：【微信公众号：通信工程师专辑】欢迎添加关注！文章转载请注明出处。