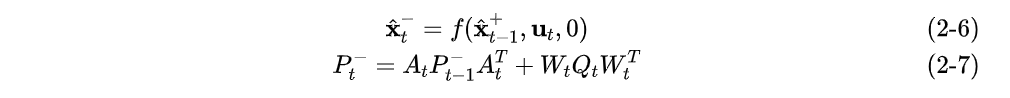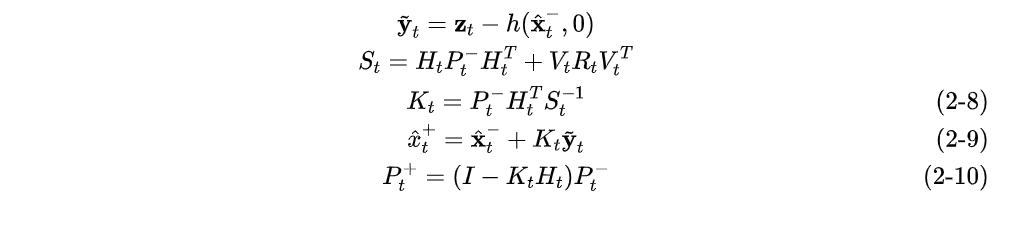卡尔曼滤波的变种有哪些?1
模拟技术
描述
1从基础卡尔曼滤波到互补卡尔曼滤波
卡尔曼滤波自从1960被Kalman发明并应用到阿波罗登月计划之后一直经久不衰,直到现在也被机器人、自动驾驶、飞行控制等领域应用。基础卡尔曼滤波只能对线性系统建模;扩展卡尔曼滤波对非线性方程做线性近似以便将卡尔曼滤波应用到非线性系统。
后来研究者发现将系统状态分成主要成分和误差,并将卡尔曼滤波用来预测误差,会使得系统的近似程度更高,效果更好。在姿态解算任务中,研究者们用辅助传感器如加速度计和磁力计来修正角速度计的积分结果,得到互补卡尔曼滤波的形式。
卡尔曼滤波是一种工具,对实际问题的不同建模方式会得到不同形式的卡尔曼滤波器。这导致了对于初学者不知道从何看起是好。另外也似乎很少有文章对基础卡尔曼滤波到各种形式的滤波形式做总结说明,于是便有了这篇文章。本文会从以下几个方面分析和讲解多种卡尔曼滤波器形式:
- 基础卡尔曼滤波 ——对线性系统的预测
- 扩展卡尔曼滤波 ——基础卡尔曼滤波在非线性系统的扩展
- 基于四元素的卡尔曼滤波器 ——基于实际问题的讲解
- 状态误差卡尔曼滤波 ——将状态误差引入状态向量
- 互补卡尔曼滤波 ——一种只使用角度误差和角速度误差作为状态向量和测量向量的滤波器形式
2符号定义
小写字母为变量;加粗小写字母为向量;大写和加粗大写为矩阵
3基础卡尔曼滤波器
宏观认识
卡尔曼滤波包含两个步骤
- 预测(prediction)—— Dynamic model
- 更新(correction/measurment update)—— Observation model
所谓 预测 ,就是用一个数学模型,根据当前的传感器输入,直接计算此时系统的状态。可以理解为一个方程的计算就行。
所谓的 更新 ,就是在某些时刻或者每一时刻,获取一些系统的其他状态输入(我们将这个值叫做 测量值 ),比较此刻预测的系统状态和测量的系统状态,对预测出的系统状态进行修正,因此也叫 测量更新 (measurment update)。
整体框架如下图所示
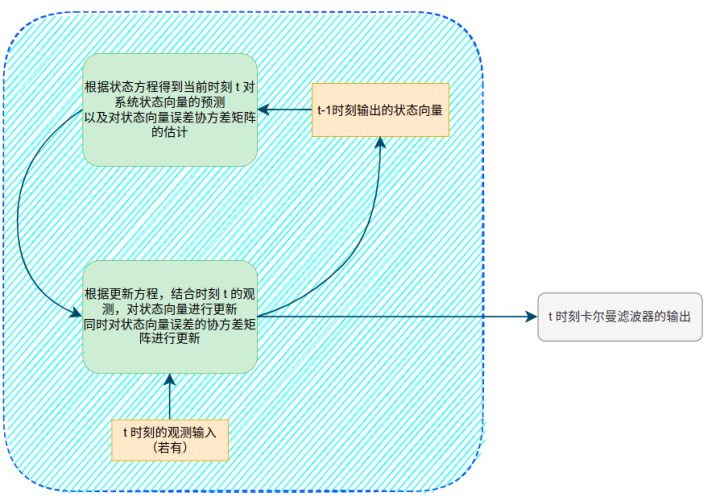
状态方程及测量方程
其中是系统状态向量,是测量向量。分别是过程噪声和观测噪声,且满足高斯分布
预测过程
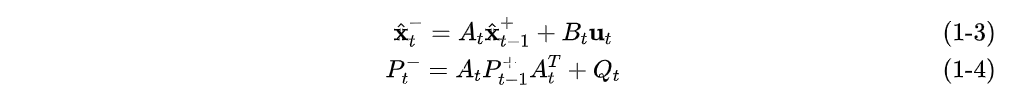
其中,是先验状态的误差协方差矩阵
更新过程
详细公式推导
本文作为一篇概述性文章,为了不使篇幅过于冗长,不进行基础卡尔曼滤波器公式的推导。想完全理解基础卡尔曼滤波器可以参考下面这几篇资料:
- 卡尔曼滤波基础知识及公式推导——较为形象化地讲解预测和更新这两个过程之间地概率分布关系
- wiki Kalman Filter——准确的公式化推导
如何理解卡尔曼滤波器?
从概率分布的角度
卡尔曼滤波器将系统状态的变化中的过程噪声假设为均值为0的高斯噪声,使得状态向量也变为一个符合高斯分布的随机向量。同时对观测过程的噪声也假设为均值为0的高斯噪声。通过测量方程,即公式(1-2)得到将状态向量映射到测量向量的函数。于是,当得到测量值的时候,可以利用测量值与状态向量之间的关系得出另外一个对状态向量的估计。利用测量值得出的状态估计和状态方程计算的状态均符合高斯分布,两个高斯分布的联合概率分布依旧保持高斯特性。进一步推导可以得到公式(1-5)到公式(1-7)。关于这个角度的理解可以阅读上面推荐的第一篇文章。
从最小化误差的角度
卡尔曼滤波的最终输出是,真实的状态为,令
对误差的平方求最小值,同样可以推导出公式(1-5)到公式(1-7)。因此卡尔曼滤波器也是系统状态的最优估计。关于这个角度的理解和推导可以参考上面推荐的第二篇文章。
4扩展卡尔曼滤波
非线性方程的线性近似
卡尔曼滤波器建立在线性的状态方程和测量方程也就是公式(1-1)和公式(1-2)。但是在实际应用中,更多的关系是非线形关系,比如如何从连续的角速度计算出车辆当前的姿态角等。为了能够利用基本卡尔曼滤波器的预测和更新过程,对于非线性的状态方程和观测方程,我们利用一阶的泰勒展开,将非线性公式近似为线性公式。
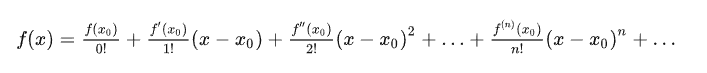
状态方程及测量方程
公式(2-1,2-2)可以类比基础卡尔曼滤波器中的公式(1-1,1-2)
一阶泰勒展开
我们先假设已知时刻滤波器的输出,也就是时刻的状态后验,以及对应的协方差矩阵为
同时,我们令的先验为
对公式(2-1)在这一点做展开,并只保留一次项
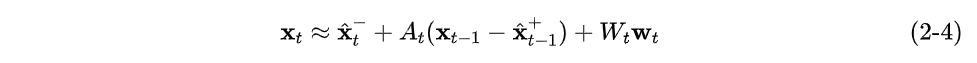
同时,对公式(2-2)在这一点做泰勒展开,并只保留一次项
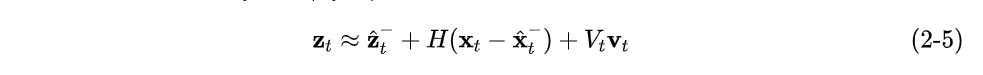
在公式(2-4)和公式(2-5)中:
预测方程及状态协方差矩阵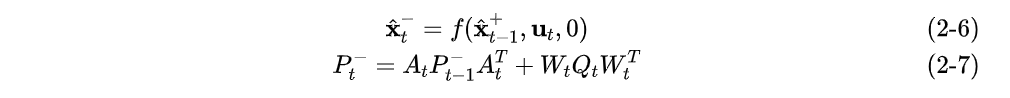
其中,公式(2-7)中的第二项,因为在线性近似方程(2-4)中,噪声项满足分布
更新方程及卡尔曼增益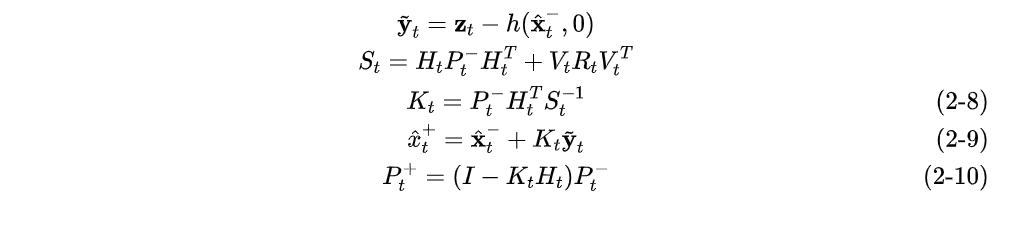
5基础卡尔曼滤波器 && 扩展卡尔曼滤波器总结
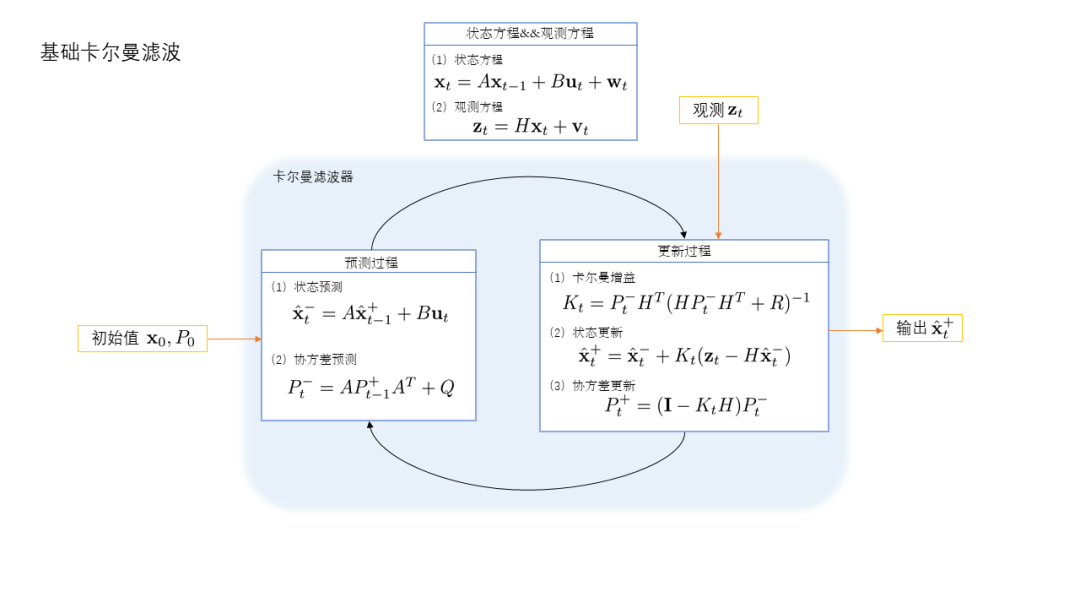
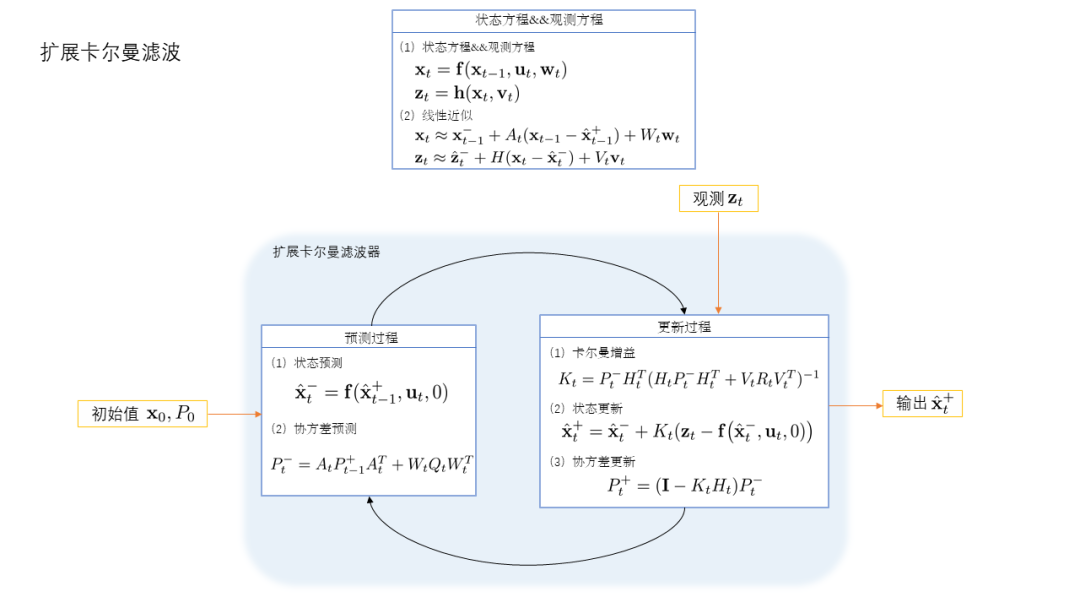
-
卡尔曼滤波基础知识2025-01-08 2114
-
卡尔曼滤波家族2024-01-14 2048
-
什么是卡尔曼滤波?卡尔曼滤波的作用是什么2023-08-08 8927
-
浅析卡尔曼滤波2023-06-14 2916
-
卡尔曼滤波(KF)与扩展卡尔曼(EKF)2023-05-10 842
-
卡尔曼滤波的变种有哪些?22023-02-13 979
-
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程2022-12-15 4471
-
扩展卡尔曼滤波的原理2022-08-12 7081
-
卡尔曼滤波原理及应用2022-06-09 581
-
卡尔曼滤波有哪些应用2021-07-12 1940
-
卡尔曼滤波算法2016-12-17 1135
-
卡尔曼滤波学习及应用2016-04-13 966
-
卡尔曼滤波2013-07-04 3061
全部0条评论

快来发表一下你的评论吧 !