

卡尔曼滤波的变种有哪些?2
模拟技术
描述
6基于四元数的拓展卡尔曼滤波器
从实际问题讲起
在运动物体的姿态估计,比如车辆的姿态计算中,常常利用IMU(Inertial Meseasurment Unit)惯性测量单元计算物体的姿态。为了方便叙述,这里的姿态估计意味着我们希望解算车辆在每一时刻与起始坐标系之间三个轴的偏转角,通常用roll、pitch、yaw表示。
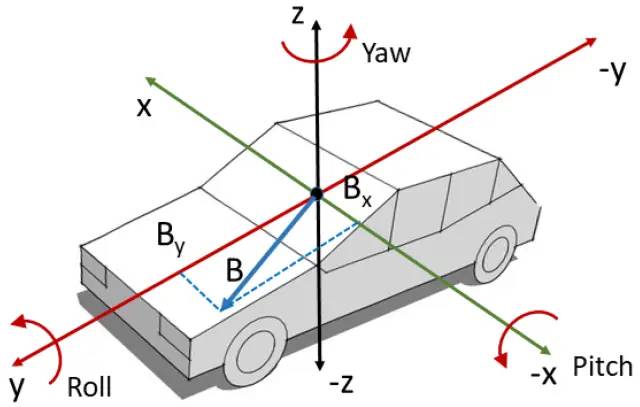
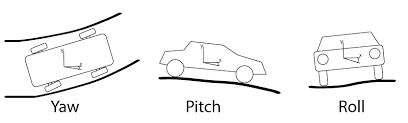
IMU(惯性测量单元)
现在的IMU一般是六轴或者九轴。六轴IMU可以输出三个轴的加速度(acc)和角速度(gyro);九轴则在六轴的基础上增加了磁力计(Magnetometer),测量三轴的磁场方向。为了简化问题,我们用六轴IMU作为示例。
相关定义
在姿态估计的各个领域中,通常使用四元数来表示一个旋转。四元数比欧拉角表达拥有更好的特性,同时相比于旋转矩阵又更加紧凑。定义四元数如下
为了估计系统的姿态,通常的做法是使用惯性测量单元IMU跟踪角速度,我们另每一时刻的角速度为
另外,我们需要知道IMU的输出频率。假设IMU的输出时间间隔为
四元素乘积的导数
这部分是为了后面推导扩展卡尔曼滤波的状态方程中的雅各比矩阵准备
我们令时刻的旋转为.时刻的旋转为。则的旋转是时刻的旋转经过的变化得到的,即
其中等于在时间间隔内的角度变化量。在极短的时间间隔内,我们认为角度的变化是匀速的,也就是。我们令在这个时间间隔内,角度的旋转轴为,旋转角度为,则
根据四元数的基础知识,我们可以得到
扩展卡尔曼滤波的重点之一在于求状态方程相对于状态的偏导;我们虽然可以从三轴角速度的输出得出角度积分的离散形式公式(1),但是我们其实不能对其直接对求偏导。至于为什么不能直接求导,下面说得挺好:
求导的定义是函数值的微增量关于自变量的微增量的极限。表示旋转的单位四元数作差后,其不再是单位四元数,也就不是旋转四元数了
为了能够对公式(1)求出偏导数,我们先求旋转相对时间的导数。然后利用泰勒展开,将公式(1)展开为线性方程,并只取一次项,这样就可以得到
我们令
则
有了角度相对于时间的导数之后,我们可以将公式(1)用泰勒展开
只保留到一次项,则我们可以得到
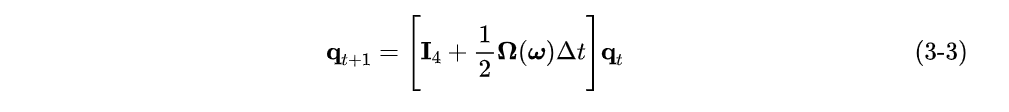
状态向量及控制输入
我们直接将车辆的姿态角以四元数形式表达作为系统状态向量
同时,将每一时刻IMU的三轴角速度作为控制输入
状态方程及其雅各比矩阵
有了上一部分关于四元素导数的推导,我们可以直接写出状态方程如下
其中是随机噪声,其协方差矩阵为
预测方程
由于在上面的推导中已经求出雅各比矩阵,所以预测方程可以直接根据拓展卡尔曼滤波公式写出来
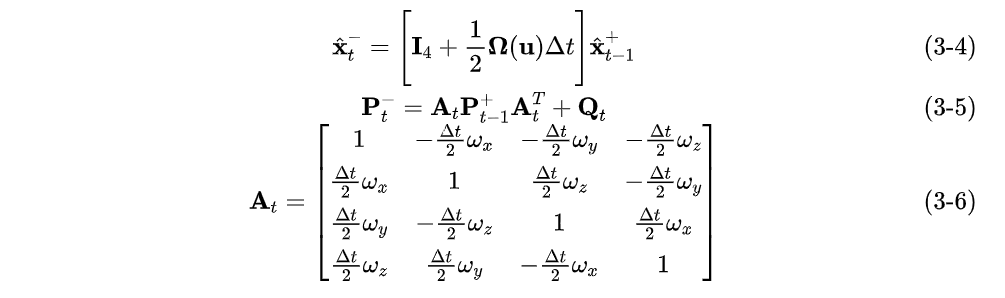
测量更新
前文我们使用了角速度计的输出作为控制输入,并构建了状态方程和预测方程。IMU通常都会有加速度计输出,这部分输出可以用来作为测量量,并对预测的状态进行测量更新。我们先回顾测量更新中状态向量的更新过程。
令加速度计的输出为测量向量:
测量模型
现在我们已经确定好了状态向量为姿态角的四元数表达,测量向量为加速度计三个轴的输出,那么函数要采用什么形式可以将姿态角转成三轴加速度呢?
其中的关键联系就是,当车辆静止时,加速度的合向量是重力加速度,垂直向下!
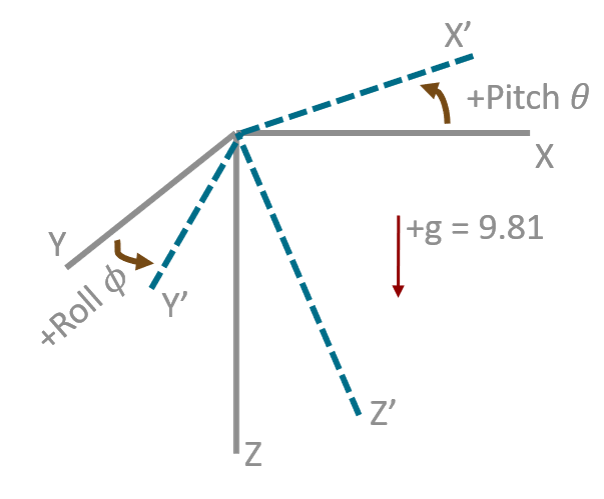
上图中,假设坐标系是起始坐标系,是小车移动后的坐标系。在起始时,小车静止,小车的重力加速度的输出是垂直向下的,即
我们采用归一化的形式,也就是将重力加速度当作一个单位。
则当小车运动后,重力加速度在坐标系下的表达为
和是重力加速度在两个不同坐标系下的表达,同时,这两个坐标系之间的旋转是此时的状态向量,因此
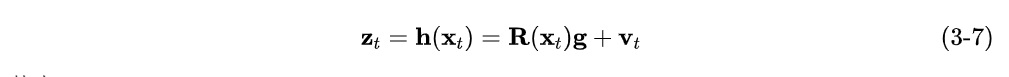
其中,
是将四元数转成旋转矩阵的表达,旋转矩阵左乘一个三位的列向量表示将该向量进行三维旋转。即下面的形式(是我们之前定义过的)
雅各比矩阵
从公式(3-7)我们可以得到测量模型中的转换函数的雅各比矩阵
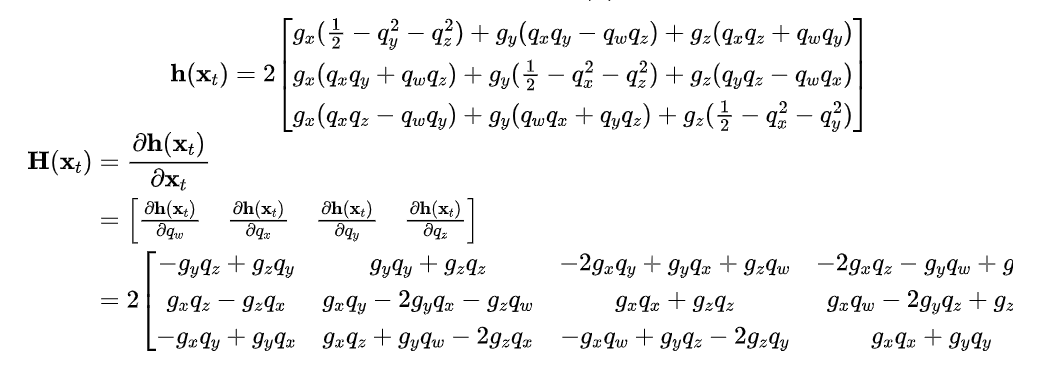
更新方程
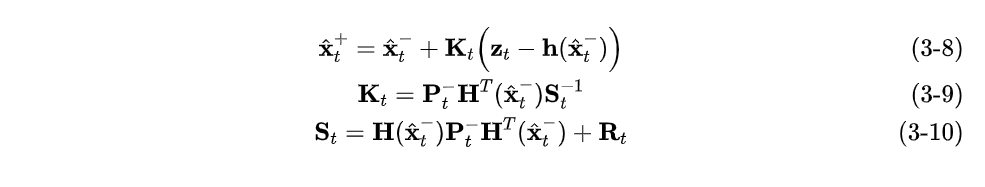
-
卡尔曼滤波基础知识2025-01-08 2114
-
卡尔曼滤波家族2024-01-14 2047
-
什么是卡尔曼滤波?卡尔曼滤波的作用是什么2023-08-08 8927
-
浅析卡尔曼滤波2023-06-14 2916
-
卡尔曼滤波(KF)与扩展卡尔曼(EKF)2023-05-10 842
-
卡尔曼滤波的变种有哪些?12023-02-13 1368
-
扩展卡尔曼滤波的原理2022-08-12 7081
-
卡尔曼滤波原理及应用2022-06-09 581
-
卡尔曼滤波有哪些应用2021-07-12 1940
-
几种最优估计和卡尔曼滤波原理的学习课件免费下载2020-05-09 1031
-
卡尔曼滤波算法2016-12-17 1135
-
卡尔曼滤波学习及应用2016-04-13 966
-
卡尔曼滤波2013-07-04 3061
全部0条评论

快来发表一下你的评论吧 !

