卡尔曼滤波的变种有哪些？4

8互补卡尔曼滤波

前言

正如前文所说，卡尔曼滤波器的建模形式多种多样，而且很多研究也是在上世纪，对于误差状态卡尔曼滤波（Error-state Kalman Filter)和互补卡尔曼滤波（Comlimentary Kalman Filter)其实没有严格的定义。这里的互补卡尔曼滤波其实也可以看成上文ErKF的另一种形式。主要采用自论文Inertial head-tracker sensor fusion by a complementary separate-bias Kalman filter。卡尔曼滤波的工作太多，博客和论文也五花八门，看起来十分不易。这篇论文从引用、论文叙述、符号标识看起来都很不错，很适合想要将卡尔曼滤波应用到姿态估计的工程师阅读。甚至有一些工作，直接使用普通卡尔曼滤波输出，然后利用互补滤波器的概念，在多种姿态输出之间做加权平均，也叫互补卡尔曼滤波器，比如这篇专利：一种基于互补卡尔曼滤波算法计算融合姿态角度的方法

互补的概念

其实只要有了角速度计（Gyroscope）我们就可以根据其输出，并在时间上做积分解算出车辆的姿态角。但是由于任何传感器都是带噪声的，同时，直接用积分解算，误差会随机时间推移而累积，最终的姿态解算精度就非常差。除了使用角速度计进行积分可以得到姿态角之外，用加速度计（Accelerometer）和磁力计（Magnatometer）也可以计算出动态系统的姿态。其中，加速度计使用重力加速度作为锚定量，测量静止状态下三轴加速度之间的夹角，可以计算出角；磁力计（或叫地磁计）利用地球磁场北极作为锚定量，可以计算出角。使用这两者对角速度计进行补充，可以得出更加准确的姿态估计。

从加速度计计算姿态角roll、pitch

加速度计（Accelerometer）可以输出三个轴的加速度，在静止的情况下，三个轴的合向量就是重力加速度。因此，我们可以利用三个轴加速度之间的关系计算静止状态下的俯仰角（pitch）和翻滚角（roll）

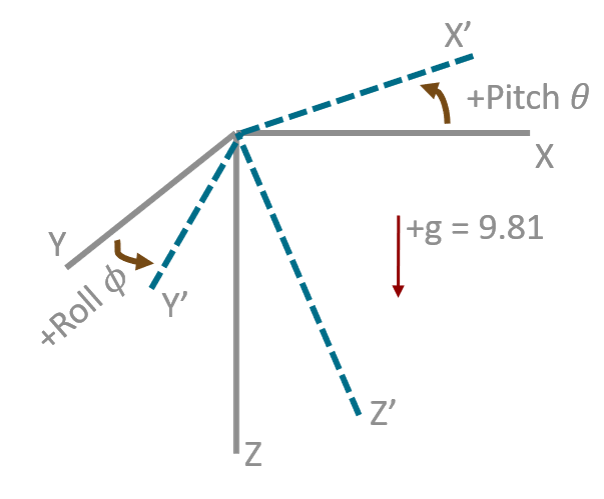
关于如何推导从三个轴的加速度计算roll和pitch，可以看这篇文章

最后得出的形式也非常简单：

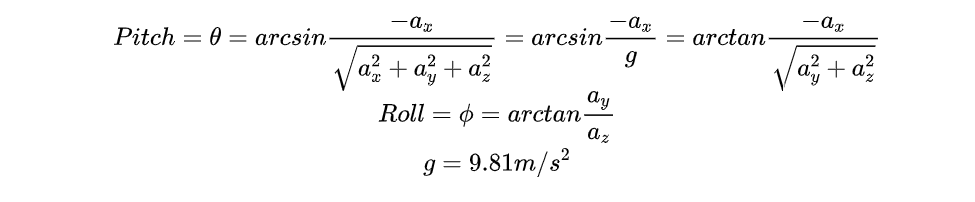
从磁力计计算姿态角yaw

磁力计的三轴合向量会指向地磁北极，利用这一特性，可以从磁力计的输出获得与地磁北极的偏转角。利用这一点，可以计算出相对于起始位置的角

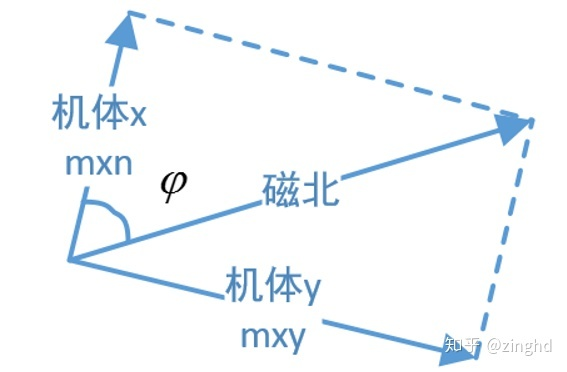
具体的计算公式可以看这篇博客

从加速度计算的姿态弥补

从加速度计可以计算出roll角和pitch角，因此，可以将这个结果和角速度的积分结果结合起来，得到一个更好的估计姿态。不过要注意的是，从加速度计算的姿态弥补有两个局限：

1. 加速度计只能计算出Roll角和Pitch角，因此yaw角无法得到互补信息
2. 当车辆处于较大的加速度运动状态时，三轴加速度的合向量跟重力加速度会有偏差，因此互补结果应该根据这个偏差的大小做改变。

互补滤波器

互补滤波器使用角速度的积分结果和加速度与磁力计的计算结果进行插值，得到更好的结果

其中，是对角速度积分得出的姿态（用四元素表达）；是使用加速度计和磁力计计算出的姿态。

互补卡尔曼滤波器

互补卡尔曼滤波器将姿态角的误差、角速度的误差当作状态向量；并利用其余传感器如加速度计和磁力计计算出的姿态角与估计的姿态角之间的差作为测量量。通过以下步骤得到系统的姿态角：

1. 卡尔曼滤波器输出姿态角的误差和角速度的误差
2. 将当前时刻角速度的输出加上角速度的误差，并利用积分公式算出姿态角
3. 将步骤2算出的姿态角加上步骤1输出的姿态角误差

状态向量和测量向量

状态向量

其中是系统的角；是三轴角速度。

测量向量

其中，是使用加速度计和磁力计计算出的系统角

状态方程

我们可以推导出姿态角对于时间的导数，通常这个导数是姿态角和角速度的函数，即

从公式（4-1）的推导过程，以及泰勒展开，我们可以得到的递推公式

我们直接假设角速度的误差是一个常量误差，即

则我们可以将上面两式写成矩阵形式

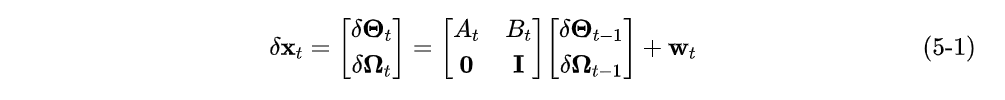
测量方程

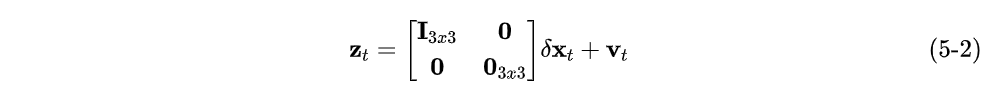
预测&&更新过程

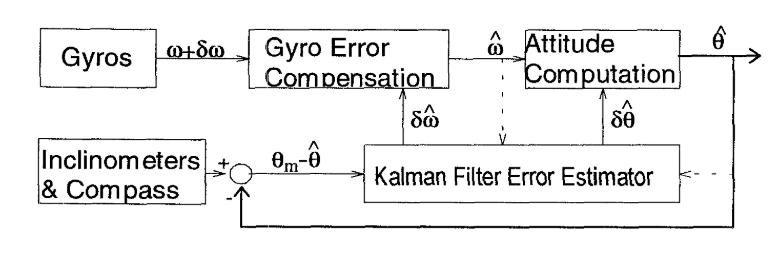
有了上面状态方程和测量方程的推导，剩下的就是按照公式（4-3）到公式（4-10）的过程代入。这里唯一不同的就是卡尔曼滤波输出的向量是角速度的误差和姿态的误差。在计算姿态的时候先将角速度的误差应用到角速度计的数据，对角度积分，将角度的误差应用到角度积分结果，得到最终的角度输出。整个框架如下图

9后话

1. 卡尔曼滤波是一个很古老的算法，但同时又是被广泛应用的算法。即使在今天姿态解算中很多用了因子图，但是对IMU的预积分依旧要使用卡尔曼滤波。但是卡尔曼滤波算法只是一个工具，不同的系统建模方式会产生不同形式的卡尔曼滤波器，这也导致了初学者不知道从哪里入手。
2. 在查资料的过程中发现，卡尔曼滤波的一些变种如Error-State Kalman Filter和Complimentary Kalman Filter其实并不是严格定义的。
3. 笔者对卡尔曼滤波并没有很丰富的应用经验，本身也不是专门做运动控制和姿态解算的。本文的叙述在追求通俗易懂之外尽力保证公式和符号定义的准确。但无法保证没有错误。
4. 对于卡尔曼滤波器中各个变量的初始值设置是门学问，论文中都会有独立的章节讲述初始值如何设置。这方面可能得结合实际应用和效果得出最优的方案。

10Reference

[1] Roll and Pitch Angles From Accelerometer Sensors

[2] 四元数、欧拉角、旋转矩阵转换

[3] 四元素乘积求导

[4] 一种基于互补卡尔曼滤波算法计算融合姿态角度的方法

[5] Inertial head-tracker sensor fusion by a complementary separate-bias Kalman filter

[6] Extended Kalman Filter vs. Error State Kalman Filter for Aircraft Attitude Estimation

[7] Kalman Filter的原始论文

[8] 卡尔曼滤波基础知识及公式推导

卡尔曼滤波的变种有哪些？1