使用CNN进行2D路径规划

本文将介绍CNN应用于解决简单的二维路径规划问题。

卷积神经网络(CNN)是解决图像分类、分割、目标检测等任务的流行模型。本文将CNN应用于解决简单的二维路径规划问题。主要使用Python, PyTorch, NumPy和OpenCV。

任务

简单地说，给定一个网格图，二维路径规划就是寻找从给定起点到所需目标位置（目标）的最短路径。机器人技术是路径规划至关重要的主要领域之一。A、D、D* lite 和相关变体等算法就是为解决此类问题而开发的。如今强化学习被广泛用于解决这一问题。本文将尝试仅使用卷积神经网络来解决简单的路径规划实例。

数据集

我们的主要问题是（在机器学习中一如既往）在哪里可以找到数据。虽然没有现成的数据集可用，但是我们可以通过制作随机二维地图创建自己的路径规划数据集。创建地图的过程非常简单：

从一个 100x100 像素的方形空矩阵 M 开始。

对于矩阵中的每一项（像素），从0到1均匀分布抽取一个随机数r。如果 r > diff，则将该像素设置为 1；否则，将其设置为 0。这里的 diff 是一个参数，表示像素成为障碍物（即无法穿越的位置）的概率，它与在该地图上找到可行路径的难度成正比。

然后让我们利用形态学来获得更类似于真实占用网格地图的“块状”效果。通过改变形态结构元素的大小和 diff 参数，能够生成具有不同难度级别的地图。

对于每张地图需要选择 2 个不同的位置：起点 (s) 和终点 (g)。该选择同样是随意的，但这次必须确保 s 和 g 之间的欧几里得距离大于给定阈值（使实例具有挑战性）。

最后需要找到从 s 到 g 的最短路径。这是我们训练的目标。所以可以直接使用了流行的 D* lite 算法。

我们生成的数据集包含大约 230k 个样本（170k 用于训练，50k 用于测试，15k 用于验证）。数据量很大，所以我使用 Boost c++ 库将自定义的 D* lite 重写为 python 扩展模块。使用这个模块，生成超过 10k 个样本/小时，而使用纯 python 实现，速率约为 1k 个样本/小时（i7–6500U 8GB 内存）。自定义 D* lite 实现的代码会在文末提供。

然后就是对数据做一些简单的检查，比如删掉余弦相似度很高，起点和终点坐标太近的地图。数据和代码也都会在文末提供。

模型架构

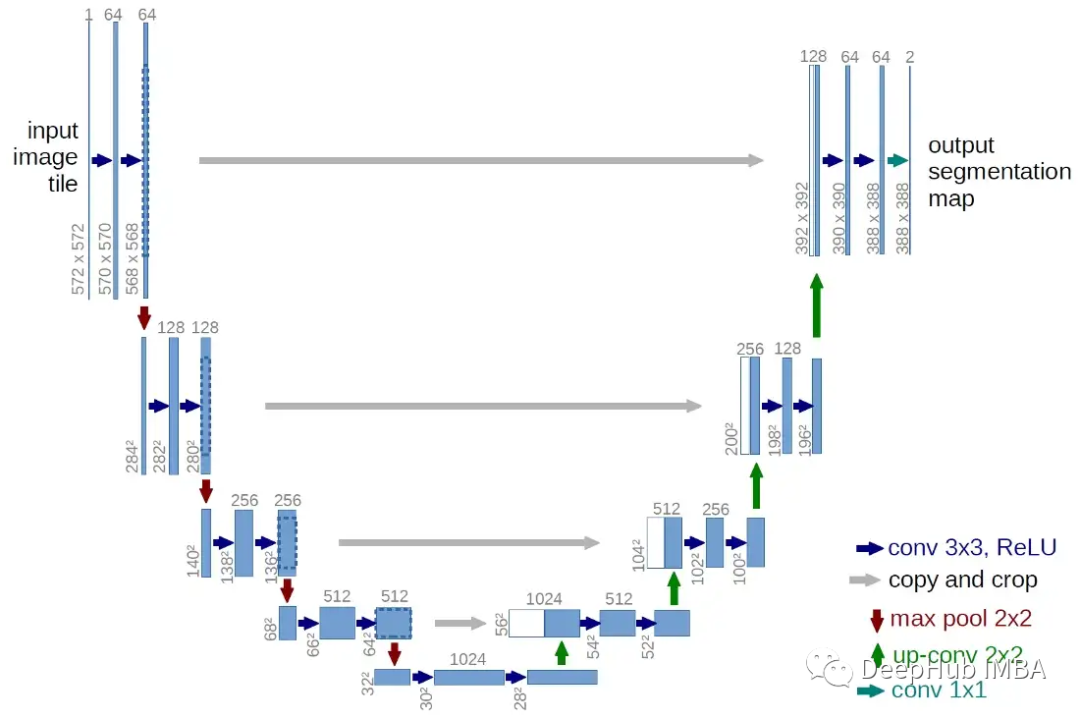
模型是经典的编码器-解码器架构，将 20 个卷积层分为 3 个卷积块（编码部分），然后是另外 3 个转置卷积块（解码部分）。每个块由 3 个 3x3 卷积层组成，每个层之间有BN和 ReLU 激活。最后，还有另外 2 个 conv 层，加上输出层。编码器的目标是找出输入压缩后的相关表示。解码器部分将尝试重建相同的输入映射，但这次嵌入的有用信息应该有助于找到从 s 到 g 的最佳路径。

该网络的输入是：

map：一个 [n, 3, 100, 100] 张量，表示占用网格图。n 是批量大小。这里的通道数是 3 而不是简单的 1。稍后会详细介绍。

start: 一个 [n, 2] 张量，包含每个地图中起点 s 的坐标

goal：一个[n, 2]张量，包含每个地图中目标点g的坐标

网络的输出层应用 sigmoid 函数，有效地提供了一个“分数图”，其中每个项目的值都在 0 和 1 之间，与属于从 s 到 g 的最短路径的概率成正比。然后可以通过从 s 开始并迭代地选择当前 8 邻域中得分最高的点来重建路径。一旦找到与 g 具有相同坐标的点，该过程就会结束。为了提高效率，我为此使用了双向搜索算法。

在模型的编码器和解码器块之间，我还插入了 2 个跳过连接。该模型现在非常类似于 U-Net 的架构。跳过连接将给定隐藏层的输出注入网络中更深的其他层。在我们的任务中关心的细节是 s、g 的确切位置，以及我们在轨迹中必须避开的所有障碍物。所以加入跳过链接大大提高了效果。

训练

在Google Colab 上对模型进行了大约 15 小时或 23 个周期的训练。使用的损失函数是均方误差 (MSE)。可能有比 MSE 更好的选择，但我一直坚持使用它，因为它简单易用。

学习率最初使用 CosineAnnealingWithWarmRestarts 调度程序设置为 0.001（略微修改以降低每次重启后的最大学习率）。批量大小设置为 160。

我尝试对输入图应用高斯模糊，并在第一个卷积层应用一个小的 dropout。这些技术都没有带来任何相关效果，所以我最终放弃了它们。

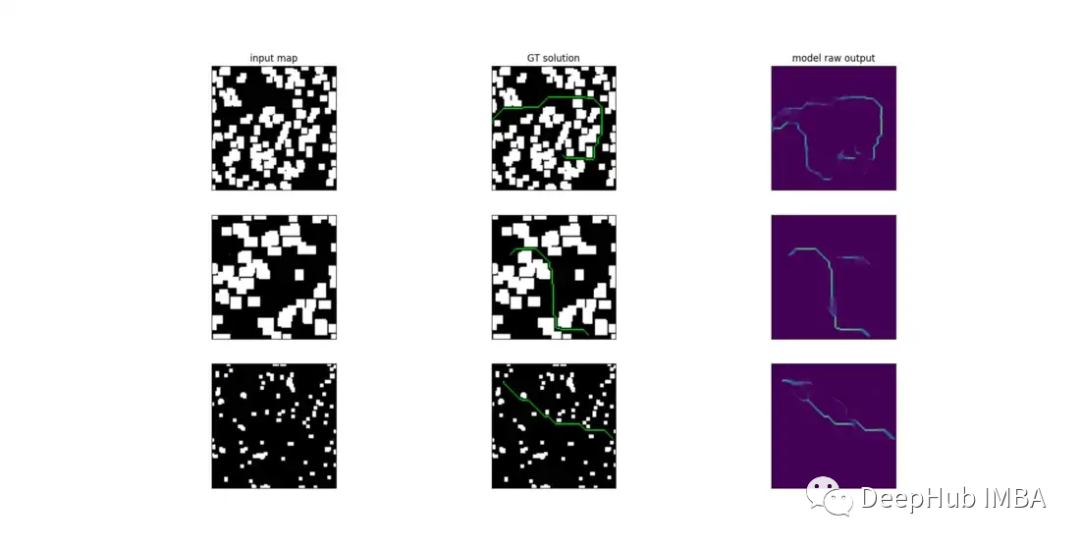
下面是训练后模型原始输出的可视化。

卷积的一些问题

起初使用输入是一个形状为 [n, 1, 100, 100]（加上起始位置和目标位置）的张量。但无法获得任何令人满意的结果。重建的路径只是完全偏离目标位置并穿过障碍物的随机轨迹。

卷积算子的一个关键特征是它是位置不变的。卷积滤波器学习的实际上是一种特定的像素模式，这种像素模式在它所训练的数据分布中反复出现。例如下面的图案可以表示角或垂直边缘。

无论过滤器学习什么模式，关键的问题是它学会独立于图像中的位置来识别它。对于像图像分类这样的任务来说，这无疑是一个理想的特性，因为在这些任务中，表征目标类的模式可能出现在图像的任何地方。但在我们的情况下，位置是至关重要的!我们需要这个网络非常清楚的知道轨迹从哪里开始，从哪里结束。

位置编码

位置编码是一种通过将数据嵌入(通常是简单的和)到数据本身中来注入关于数据位置的信息的技术。它通常应用于自然语言处理(NLP)中，使模型意识到句子中单词的位置。我想这样的东西对我们的任务也有帮助。

我通过在输入占用图中添加这样的位置编码进行了一些实验，但效果并不好。可能是因为通过添加关于地图上每个可能位置的信息，违背了卷积的位置不变性，所以滤波器现在是无用的。

所以这里基于对路径规划的观察，我们对绝对位置不感兴趣，而只对相对范围感兴趣。也就是说，我们感兴趣的是占用图中每个单元格相对于起点s和目标点g的位置。例如，以坐标(x, y)为单元格。我并不真正关心(x, y)是否等于(45,89)还是(0,5)。我们关心的是(x, y)距离s 34格，距离g15格。

所以我为每个占用网格图创建2个额外的通道，现在它的形状为[3,100,100] 。第一个通道是图像。第二个通道表示一个位置编码，它为每个像素分配一个相对于起始位置的值。第三通道则是相对于结束位置的值。这样的编码是通过分别从以s和g为中心的二维高斯函数创建2个特征映射来实现的。Sigma被选为核大小的五分之一(通常在高斯滤波器中)。在我们的例子中是20，地图大小是100。

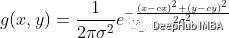
在注入关于期望的轨迹起始和最终位置的有用信息的同时，我们还部分地保留了与过滤器位置不变性的一致性。可学习的模式现在只依赖于相对于给定点的距离，而不是地图上每个可能的位置。距离s或g相同距离的2个相等的图案现在将触发相同的过滤器激活。经过实验这个小技巧在收敛训练中非常有效。

结果和结论

通过测试了超过 51103 个样本的训练模型。

95% 的总测试样本能够使用双向搜索提供解决方案。也就是说，该算法使用模型给出的得分图可以在 48556 个样本中找到从 s 到 g 的路径，而对于其余 2547 个样本则无法找到。

总测试样本的 87% 提供了有效的解决方案。也就是说从 s 到 g 的轨迹不穿越任何障碍物（该值不考虑 1 个单元格的障碍物边缘约束）。

在有效样本上，真实路径与模型提供的解决方案之间的平均误差为 33 个单元格。考虑到地图是 100x100 单元格，这是相当高的。错误范围从最小 0（即，在 2491 个样本中的真实路径被“完美”的重建了）到最大……745 个单元（这个肯定还有一些问题）。

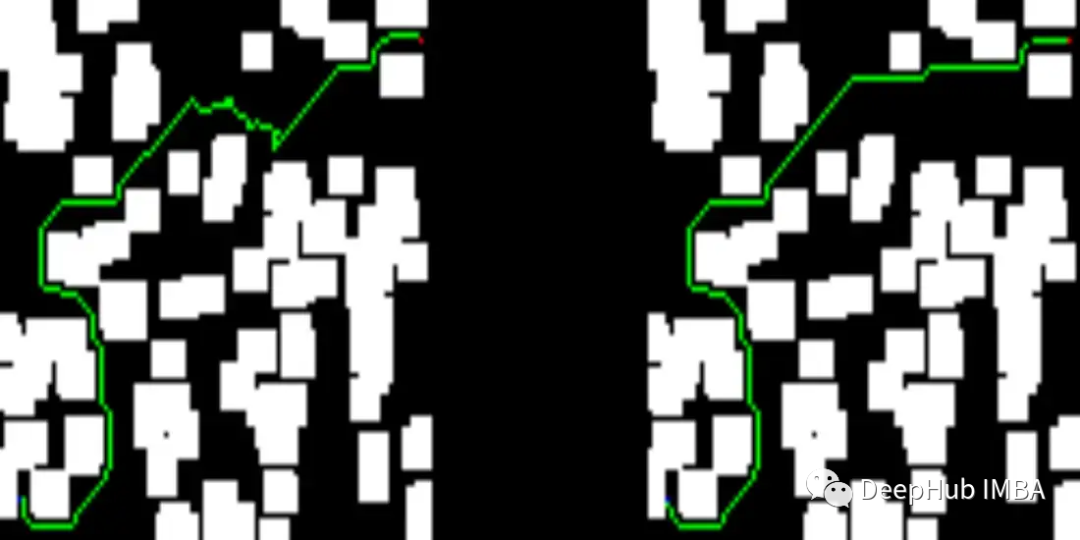
下面可以看看我们测试集中的一些结果。图像的左侧描述了训练过的网络提供的解决方案，而右侧显示了D* lite算法的解决方案。

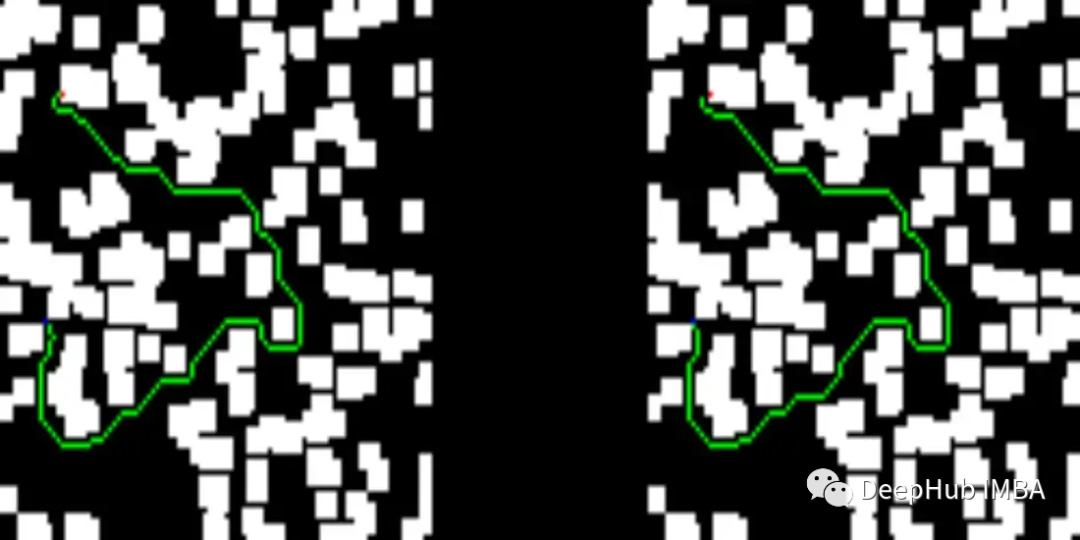
我们网络提供的解决方案比D* lite给出的解决方案短：

下面就是一些错误的图：

看着应该是感受野不太大，所以在感受野的区域内没有找到任何的边缘，这个可能还要再改进模型。