FPGA的算法解析1:整数操作与加减法器

一. 整数的概念

整数在 IEEE 的规定上有短整数 short integer , 中整数 integer 和 长整数 long integer ，它们之间的关系如下：

为了方便讨论，下面均以短整数作为例子。

原码：最高为符号位，之后是数值位。

 

+62 的原码表示为 00111110
-62 的原码表示为 10111110

 

补码：正数和0的补码与原码相同，负数的补码是将其原码的符号位保持不变，对数值位逐位求反，然后在最低位加一。对补码求补就可以得到原码。

 

+6 的原码表示为 00000110            +6 的补码表示为 00000110 
-5 的原码表示为 10000101            -5 的补码表示为 11111011

 

补码的运算规则：在FPGA的底层，有符号数都是按照补码来存储的。补码有一个特别的好处就是可以将减法转换为加法，从而将加减法统一。

 

7-5：
7 的补码是 00000111，-5 的补码是 11111011 ,7 + (-5) = 00000111 + 11111011 = (1)00000010
由于只有8位，因此将进位舍去得到加和的结果为 00000010，恰好是 2 的补码
3-4：
3 的补码是 00000011，-4 的补码是 11111100 ,3 + (-4) = 00000011 + 11111100 = 11111111
得到加和的结果为 11111111，恰好是 -1 的补码

 

溢出：两个补码相加时，如果产生的和超出了有效数字位所表示的范围，则计算结果会出错，解决的方法是扩大字长。

二. 简单的加法与减法操作

通过上面的讨论，我们可以很容易的看到，从理论上讲在底层对补码只用加法就可以完成加法与减法的操作，但是由于我们在上层是对行为进行描述，因此也是要用到减法的。

 

module adder8(sum,ina,inb);
// 定义输入输出变量,这个加法器不考虑进位，只需要对输入数据进行最高位扩展
output [8:0] sum;
input [7:0] ina,inb;
assign sum = {ina[7], ina} + {inb[7],inb};
endmodule

 

 

module subber8(dif,ina,inb);
        // 定义输入输出变量,这个减法器不考虑借位，只需要对输入数据进行最高位扩展
output [8:0] dif;
input [7:0] ina,inb;
assign dif = {ina[7], ina} - {inb[7],inb};
endmodule

 

这是对有符号数设计的加减法器，可以看到上面的加减法都完成的很棒，并没有产生溢出的问题。

三. 采用流水线操作的加法器（耗时角度考虑）

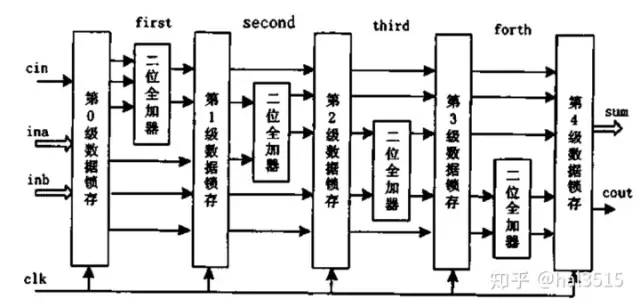
这是一个四级流水线加法器的框图，上面的加法器采用5级锁存、4级加法的结构。每一个加法器实现2位数据和上一个进位的相加，整个加法器只受2位全加器的工作速度的限制，平均完成一个加法运算只需要一个时钟周期的时间，需要注意的是由于有四级流水线，因此这个加法器在输出第一个计算值的时候有四个时钟周期的延时。这里只给出无符号数的流水线加法器的模型，都写出来太长了（其实我也没有写 ）。代码写的比较繁琐，但是逻辑更清楚，主要是当做学习流水线结构的例子，真正在工程中用的话感觉还是调IP核吧。

 

module pipeadder8(cout,sum,ina,inb,cin,clk,rst_n);
// 定义输入输出变量
output [7:0] sum;
output cout;
input [7:0] ina,inb;
input cin,clk,rst_n;
reg [7:0] tmpa,tmpb,sum;
reg cout;
reg tmpci,firstco,secondco,thirdco;
reg[1:0] firsts;
reg[5:0] firsta,firstb;
reg[3:0] seconds;
reg[3:0] seconda,secondb;
reg[5:0] thirds;
reg[1:0] thirda, thirdb;
// 这里进行第0级数据缓存
always@(posedge clk or negedge rst_n) begin
if(!rst_n) {tmpa,tmpb,tmpci} <= {8'd0,8'd0,1'b0};
else {tmpa,tmpb,tmpci} <= {ina,inb,cin};
end
// 这里进行第1级数据缓存，并且完成最低两位以及进位位的加法
always@(posedge clk or negedge rst_n) begin
if(!rst_n) {firstco,firsts,firsta,firstb} = {1'b0,2'd0,6'd0,6'd0};
else begin
{firstco,firsts} <= tmpa[1:0] + tmpb[1:0] + tmpci;
firsta <= tmpa[7:2];
firstb <= tmpb[7:2];
end
end
// 这里进行第2级数据缓存，并且完成次低两位以及进位位的加法
always@(posedge clk or negedge rst_n) begin
if(!rst_n) {secondco,seconds,seconda,secondb} = {1'b0,4'd0,4'd0,4'd0};
else begin
{secondco,seconds} <= {{1'b0,firsta[1:0]} + {1'b0,firstb[1:0]} + firstco, firsts};
seconda <= firsta[5:2];
secondb <= firstb[5:2];
end
end
// 这里进行第3级数据缓存，并且完成次次低两位以及进位位的加法
always@(posedge clk or negedge rst_n) begin
if(!rst_n) {thirdco,thirds,thirda,thirdb} = {1'b0,6'd0,2'd0,2'd0};
else begin
{thirdco,thirds} <= {{1'b0,seconda[1:0]} + {1'b0,secondb[1:0]} + secondco, seconds};
thirda <= seconda[3:2];
thirdb <= secondb[3:2];
end
end
// 这里进行第4级数据缓存，并且完成次次次低两位以及进位位的加法
always@(posedge clk or negedge rst_n) begin
if(!rst_n) {cout,sum} = {1'b0,8'd0};
else {cout,sum} <= {{1'b0,thirda[1:0]} + {1'b0,thirdb[1:0]} + thirdco, thirds};
end


endmodule