

什么是频谱,为什么要对它进行分析?
电子说
描述
我们已经习惯于用时间作为参照,来记录某时刻发生的事件。这种方法当然也适用于电信号。于是可以用示波器来观察某个电信号(或通过适当传感器能转换成电压的其他信号)的瞬时值随时间的变化,也就是在时域中用示波器观察信号的波形。
然而,傅立叶理论 (Jean Baptiste Joseph Fourier,1768-1830。他提出任何周期信号都可以看做是一系列正弦波和余弦波的叠加。)告诉我们,时域中的任何电信号都可以由一个或多个具有适当频率、幅度和相位的正弦波叠加而成。
换句话说,任何时域信号都可以变换成相应的频域信号,通过频域测量可以得到信号在某个特定频率上的能量值。通过适当的滤波,我们能将图 1-1 中的波形分解成若干个独立的正弦波或频谱分量,然后就可以对它们进行单独分析。每个正弦波都用幅度和相位加以表征。
如果我们要分析的信号是周期信号,傅立叶理论指出,所包含的正弦波的频域间隔是 1/T,其中 T 是信号的周期 (若时间信号只出现一次,则 T 为无穷大,在频域中用一系列连续的正弦波表示。)
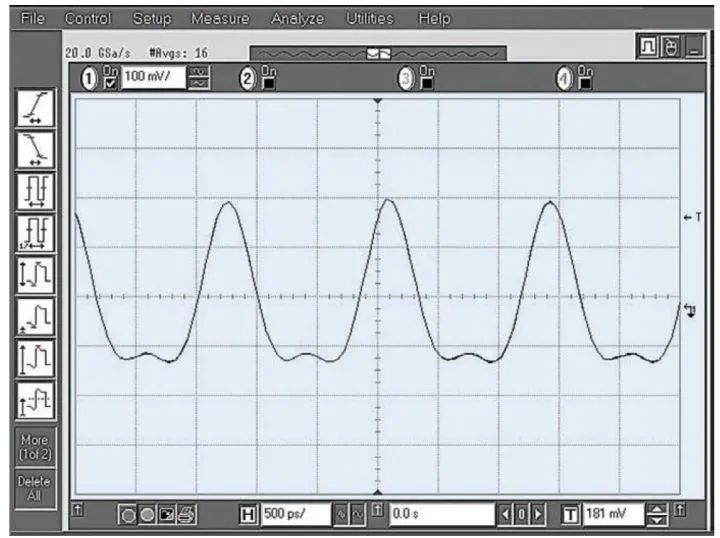
图 1-1. 复合时域信号
某些测量场合要求我们考察信号的全部信息 — 频率,幅度和相位,然而,即便不知道各正弦分量间的相位关系,我们也同样能实施许多的信号测量,这种分析信号的方法称为信号的频谱分析。
频谱分析更容易理解,而且非常实用。您可以了解如何使用频谱分析仪进行信号的频谱分析。为了正确地从时域变换到频域,理论上必须涉及信号在整个时间范围、即在正负无穷大的范围内的各时刻的值,不过在实际测量时我们通常只取一段有限的时间长度。
按照傅立叶变换理论,信号同样也可以从频域变换到时域,当然,这涉及理论上在正负无穷大的频率范围内对信号的所有频谱分量值作出估计。实际上,在有限带宽内进行的测量获取了信号的大部分能量,其结果是令人满意的。在对频域数据进行傅立叶变换时,各个频谱分量的相位也成为至关重要的参数。例如,在把方波变换到频域时如果不保存相位信息,再变换回来的波形可能就是锯齿波了。
什么是频谱?
那么,在上述讨论中什么是频谱呢?正确的回答是:频谱是一组正弦波,经适当组合后,形成被考察的时域信号。图 1-1 显示了一个复合信号的波形。假定我们希望看到的是正弦波,但显然图示信号并不是纯粹的正弦形,而仅靠观察又很难确定其中的原因,什么是 动态频谱共享?
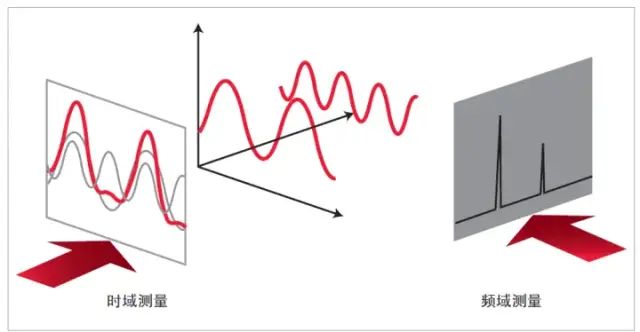
图 1-2. 信号的时域和频域关系
上图同时在时域和频域显示了这个复合信号。频域图形描绘了频谱中每个正弦波的幅度随频率的变化情况。如图所示,在这种情况下,信号频谱正好由两个正弦波组成。
现在我们便知道了为何原始信号不是纯正弦波,因为它还包含第二个正弦分量,在这种情况下是二次谐波。既然如此,时域测量是否过时了呢?答案是否定的。时域测量能够更好的适用于某些测量场合,而且有些测量也只能在时域中进行。例如纯时域测量中所包括的脉冲上升和下降时间、过冲和振铃等。
审核编辑:汤梓红
-
如何使用DFT进行频谱分析2024-12-20 2853
-
如何使用傅立叶变换进行频谱分析2024-12-06 2123
-
如何对电磁频谱系统特征进行分析2024-11-27 861
-
频谱分析仪检定规程标准2024-06-03 1718
-
频谱分析仪的用途与应用详解2024-05-14 4309
-
频谱分析仪的常见误差来源 频谱分析仪的校准方法2023-12-21 2906
-
频谱分析仪应用于新能源汽车频谱分析与噪声测量的应用场景2023-04-27 1102
-
为何要对频谱分析仪校准功率?2023-02-24 1143
-
如何对CDAQ模块采集的信号进行FFT频谱分析2017-12-27 2947
-
有关频谱分析问题2016-04-10 2406
-
更好地进行频谱分析的几点提示2009-11-04 624
-
用FFT对信号进行频谱分析的实验2009-05-12 23142
-
使用实时频谱分析仪进行RFID和NFC测量2008-10-12 1039
全部0条评论

快来发表一下你的评论吧 !

