

典型二级运放的稳定性分析
模拟技术
描述
经典手算法设计二级运放
手算法其实就是根据设计要求,把结构定下来之后运用运放的一些基础知识将MOS管的W/L参数一一定下来的方法,这个方法不一定能设计出很完美的运放,但是对运放的深入理解是很有帮助的。
二级运放涉及参数——这些参数决定着一个运放的优劣,但更重要的是根据不同的场合来选择合适的运放(参数定义有不清楚的请自行翻书):
1、增益
增益
2、单位增益带宽(GB)
单位增益带宽
3、沉降时间
稳定时间
4、压摆率
摆率
5、输入共模范围
共模输入范围
6、共模抑制比
共模抑制比
7、电源抑制比
电源抑制比
8、输出电压摆幅
输出摆率
9、输出电阻
输出阻抗
10、胶印
失调电压
11、噪音
噪声
12、布局区域
版图面积
上述参数只涉及运放设计的一部分要求,而对运放来说,稳定性是其最基础而又最重要的要求。 上述参数并未涉及到稳定性相关参数,下面对典型二级运放的稳定性进行一些基础分析。
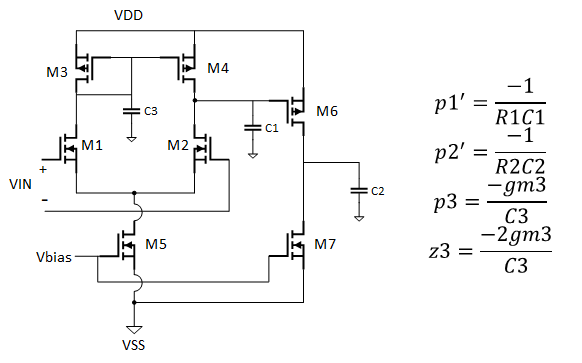
上图为没有进行补偿的二级运放示意图,其中C1、C3为寄生电容,C2为寄生电容+负载电容。
因此图中主要存在3个极点和1个零点,分别罗列在上图右侧,其中p3与z3分别为镜像极点与镜像零点(为啥叫镜像? 估计因为是电流镜M3、M4栅极节点上的?),且通常p3、z3远大于GB,对运放的稳定性影响很小; p3、z3相距较近,趋向相互抵消。 剩下的p1’、p2‘两个主次极点由于相距相对较近,频率也不大,因此对运放的稳定性影响较大。
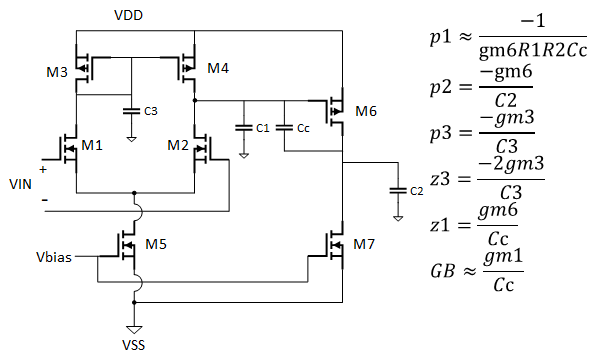
上图为补偿后的二级运放示意图,其中Cc为米勒补偿电容。
同图1,p3、z3对运放的稳定性影响很小,但其主次极点发生了变化,实现了极点分裂,分别为上图右侧的p1与p2,极点的分裂给运放的稳定性带来了正面的效果。 在该二级运放中,还引入了右半平面的零点z1,这可能会给稳定性带来影响。
上述公式中,GB=|p1|×GAIN≈gm1/Cc。
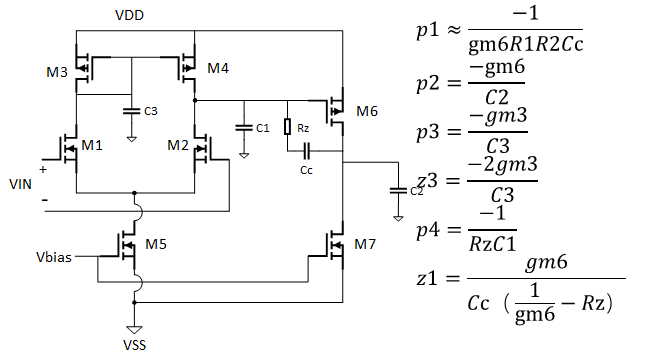
上图为带调零电阻的补偿后的二级运放示意图,其中Rz为调零电阻,Rz可以使运放更加稳定。
由图2可知,零点z1会给运放的稳定性带来影响,而Rz的出现,使零点z1发生了改变。 此时只需调整Rz的大小,使1/gm6-Rz=0,零点z1就可以移动至无穷大; 也可以将其从右半平面移动到左半平面并与p2抵消。 在实际设计时,我们也可以采用上述方法利用Rz来减小对运放稳定性影响的,如通过仿真得到gm6的值,再取其倒数估算Rz的大小。
前面给出了同一结构的运放在不同补偿条件下的零极点,下面就来总结一下什么样的零极点对运放来说才是稳定的。
说到零极点与稳定性,就能联想到波特图,下面就结合波特图直接从结论推出我们想要的结论:
1、在波特图中,每个零点频率处,幅值曲线的斜率按+20dB/dec变化,每个极点频率处,幅值曲线的斜率按-20dB/dec变化。
2、对一个ωm的极点(零点)频率,相位约在0.1ωm的地方开始下降(上升),在ωm处经历-45°(+45°)的变化,在大约10ωm处达到-90°(+90°)的变化。
3、高频极点和零点对相位的影响可能比对幅值的影响更大。
4、在稳定系统中,增益交点(GX)必定发生在相位交点(PX)之前,增益交点指的是环路增益的幅值等于1
的频率,相位交点指的是环路增益的相位等于-180°的频率。 GX对应频率与单位增益带宽相同。
5、GX与PX的间距越大,反馈系统越稳定。
6、相位裕度(PM)=180°+∠βH(ω=ω1),其中ω1是GX频率。 当PM≥60°,系统被认为是稳定的。
由1~6可知:
1、对于一个单极点系统是无条件稳定的,因为单个极点不可能产生大于90°的相移。
2、对于一个双极点系统,当GX对应的频率正好是第二极点时,可以证明此时的PM=45°。 因此为确保PM≥60°,第二极点必须出现在GX频率之后(约2.2~3倍GB处)。
3、对于除了主次极点外其他会影响稳定性的零极点,我们希望其频率>10GB。
下面就根据以上分析,正式进入今天的主题:设计一个满足要求的二级运放。
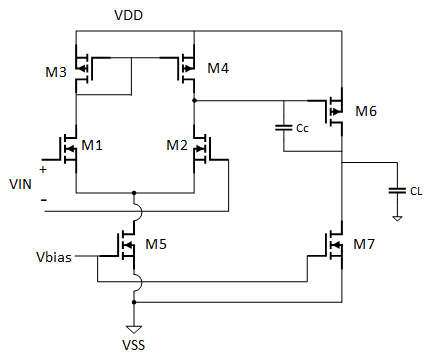
设计案例
设计如上图所示的二级运放,条件如下:
Av>3000V/V,VDD=5V,VSS=0V,GB=5MHz,SR>10V/us,PM=60°,ICMR=1.5~4.5V,
输出电压范围=0.5~4.5V,功率≤2mW,CL=10pF
设计步骤:
①首先选择合适的工艺,假设该工艺kn=110uA/V²,kp=50uA/V²,VTN=0.55V,VTP=0.85V.
②由60°PM可知:|p2|>2.2GB且|z1|>10GB,因此gm6/CL>2.2gm1/Cc且gm6/Cc>10gm1/Cc,因此gm6>10gm1→1/CL>0.22/Cc→Cc>0.22CL=2.2pF,这里取Cc=3pF。
(3)∵SR=Id5/Cc>10V/us→
Id5>10V/us×3pF=30uA,取I5=30uA。
(4)∵GB=gm1/Cc=5MHz→gm1=15*2π=94.2uS
∵gm=√(2kn *W/L *I) →W/L=2.69≈3
于是可以得到M1、M2管的宽长,取W/L=6um/2um。
⑤∵ICMR_max=4.5V→Vov3_min=VDD-(ICMR_max-VTN)-VTP=5-(4.5-0.55)-0.85=0.2V,若此时M3仍饱和,则满足平方律公式,且Id3=15uA,由此可推出M3、M4的宽长比W/L=2Id/(kp*Vov²)=15,
取W/L=30um/2um。
⑥∵ICMR_min=1.5V→若要确保M5进入饱和状态,Vov5_min=Vds5=ICMR_min-(Vov1+VTN)=1.5-(√(2I/(kn*W/L))+0.55)=0.65V,且Id5=30uA,由此可推出M5的宽长比W/L=2Id/(kp*Vov²)=1.29≈1.5,取W/L=3um/2um。
⑦∵gm6>10gm1,取gm6=942uS。 由于稳态时VGS4=VGS6,且gm=k*W/L*Vov,因此gm6/gm4=(W/L)6/(W/L)4→(W/L)6=gm6/gm4*(W/L)4=942uS/√(2kp *(W/L)4*Id4)*15=94.2,取W/L=188um/2um。
⑧由gm=√(2k *W/L*I)→Id6=94.4uA,因此可得到M7的宽长比(W/L)7=(W/L)5*94.4/30=4.7,取W/L=10um/2um。
⑨∵Vov=2Id/gm=√(2Id/(k*W/L)),∴Vov6=0.2V,Vov7=0.58V,由此可得输出电压最大值为5-0.2=4.8V>4.5V,而最小输出电压为0.58V>0.5V,不符合最小输出电压范围,此时可选择适当增大M7管的宽长比。
(10)Av=gm1/(Id5/2*(l2+λ4))gm6/(Id6(λ6+λ7))=7736>3000V/V,因此增益符合要求。
Pdiss=5V*(30+94.4)uA=0.62mW<2mW,因此功耗也符合要求。
以上是对典型二级运放的一个粗略的设计,最后可以将计算出的运放尺寸代入仿真模型,通过电路仿真来验证其是否满设计要求,并做最后的优化。 在实际设计过程中不难发现,一些与工艺相关的参数是不容易找到的,最终还是要通过代入工艺模型来进行多次的仿真调整,才能得到比较可靠的结果。
-
TINA可以进行运放的稳定性分析吗?2024-09-04 279
-
运放系统稳定性原理 运放的频率补偿2023-10-25 1753
-
运放的稳定性仿真分析2023-10-16 2653
-
运放的基本原理和稳定性分析2023-07-24 4477
-
开关电源环路稳定性分析(二)2022-11-22 6705
-
关于电源/负载电路组合的稳定性分析2021-05-11 2332
-
资深工程师教你,轻松实现运放负反馈电路稳定性2020-10-03 3175
-
开关电源环路稳定性分析2020-05-31 3910
-
运放稳定性分析详解(五)2016-08-08 908
-
【运放稳定性分析】TI 高精度实验室 运放培训笔记2016-04-03 4741
-
运放稳定性分析2016-02-19 966
-
LDO稳定性分析2011-11-01 859
-
频率响应法-相对稳定性分析2009-07-27 3406
-
典型二阶系统设计及其瞬态响应和稳定性分析2008-10-16 14889
全部0条评论

快来发表一下你的评论吧 !

