从泊松方程的解法，聊到泊松图像融合

 

泊松融合（Poisson Blending）又作 Seamless clone，用于将两幅图像“无缝”的融合起来，基本原理就是最优化一个方程，尽量在和base边界处保持相关的亮度，同时保留剪切过来图像的梯度，这样看起来两张图像就“无缝”拼合在一起了。  

 

2004 年 SIGGRAPH 上，Microsoft Research UK 有篇经典的图像融合文章《Poisson Image Editing》。先看看其惊人的融合结果（非论文配图，本人实验结果）：

这篇文章的实现，无关目前算法领域大火的神经网络，而是基于泊松方程推导得出。

 

泊松方程是什么？

 

很多朋友比较熟悉概率论里面的泊松分布。泊松方程，也是同一个数学家泊松发明的。但却和泊松分布没有什么关系，是泊松物理学领域提出的一个偏微分方程。

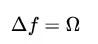
这里表示的是拉普拉斯算子，和在泊松方程中是已知量，可以是实数或复数值方程，特殊情况当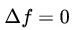时被称为拉普拉斯方程。当处于欧几里得空间时，拉普拉斯算子通常表示为。

学习图像处理的朋友对于和比较熟悉，分别表示二阶微分（直角坐标系下的散度）、一阶微分（直角坐标系下的梯度）。

 

微分与卷积

 

连续空间中的微分计算，就是大学里微积分那一套公式。但是在计算机的世界里，数据都是在离散空间中进行表示，对于图像而言，基本的计算单元就是像素点。让我们从最简单的情形，一维数组的微分说起：

表示位置 x 一阶微分计算（一阶中心导）： 

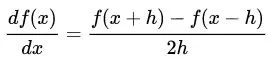
表示位置 x 二阶微分计算（二阶中心导）： 

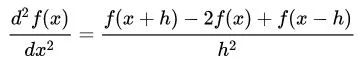
随着h->0，上面的微分算式的结果会逐渐逼近真实的微分值。对于图像而言，这里 h 最小可分割单元是像素，也就表示像素间的间距，可视为 1。再看看，二阶微分的公式，是不是可以看成 1x3 的卷积核 [1，-2，1] 在一维数组上进行卷积计算的结果（卷积中心在 x 上）。

至此，不难理解，离散数据（例如图像）上的微分操作完全可以转换为卷积操作。

当数组维度更高，变成二维数组呢？也就是处理图像的拉普拉斯算子： 

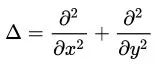
此时，卷积核尺寸应该是 3x3，具体数值为

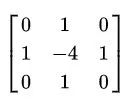
称为拉普拉斯卷积核。

记住拉普拉斯卷积核，我们后面会用到。

 

泊松方程求解

 

这个时候，想想我们学会了什么？泊松方程的形式，以及拉普拉斯卷积核。

再想想，在图像场景下，什么是泊松方程的核心问题？

已知图像点二阶微分值（直角坐标系下即散度div）的情况下，求解各个图像点的像素值。

一个简单的例子，假设有一张 4x4 的图像 x：

Xi表示各个位置上的图像像素值，共 16 个未知参数需要被求解。

应用拉普拉斯卷积核后，得到 4 个方程式：

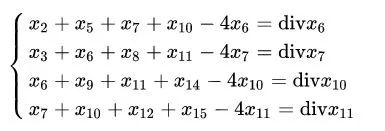
4 个方程式求解出 16 个未知参数？这是不可能的。

因此，我们需要另加入至少 12 个更多的方程式，也就是说，需要把剩余 12 个边界点的值确定，即需要确定边界条件。边界一般符合 2 种常见的边界条件：

Neumann 边界，译为纽曼边界或黎曼边界，给出函数在边界处的二阶导数值；

Dirichlet 边界，狄利克雷边界，给出边界处函数在边界处的实际值。

但给定边界条件之后，就可以有 16 个方程式组成的方程组了，矩阵化表示此方程组之后，得到形式为 Ax=b。

看到 Ax=b，大家就应该放松了，不就是解方程嘛，用雅可比迭代法或者高斯赛德尔迭代法来求解就 OK 了。

 

Poisson Image Editing

 

背景知识储备好了后，让我们把目光拉回到论文《Poisson Image Editing》上。

在图像融合任务中，前景放置在背景上时，需要保证两点：

前景本身主要内容相比于背景而言，尽量平滑；

边界处无缝，即前景、背景在边界点位置上的像素值，需要保持边界一致。

重点关注两个词：内容平滑、边界一致。平滑是什么？可以理解成图像前景、背景梯度相同。边界一致是指什么？可以理解成在边界上像素值相同。再用一张图来说明：

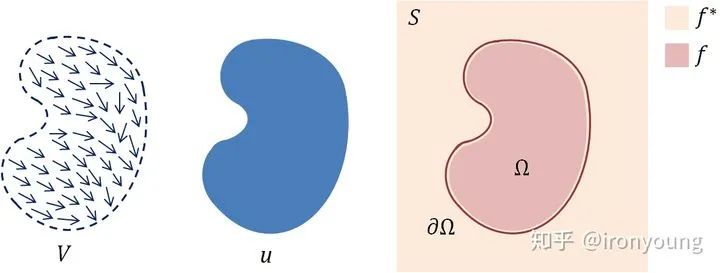
蓝色图片表示前景图片，需要被融合到肉色的背景图片上

上图中 u 表示需要被合成的前景图片， V 是u的梯度场。S是背景图片， 是合并后目标图像中被前景所覆盖的区域，则  是  的边界。设合并后图像在 内的像素表示函数是 ，在  外的像素值表示函数是  。

此时，平滑可表示为： 

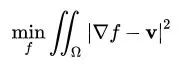
 保持边界一致可表示为：  

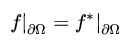
这里如果接触过泛函的朋友会比较开心，没接触过的朋友可以先看看欧拉-拉格朗日方程。令

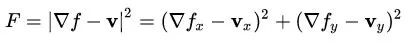
代入欧拉-拉格朗日方程后则有：

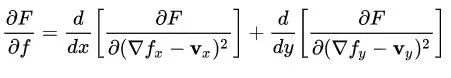
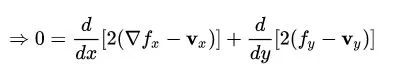
怎么样，看起来是不是一个泊松方程呢？当然，还差两步：

因为需要平滑， div v 取值需要同时参考前景图片和背景图片，可以直接等于前景像素的散度，也可以在前景和背景在同一点像素的散度进行某种组合得到（论文中在 Selection cloning 和 Selection editing 章节有讨论各自合适的场景，但个人以为这里采取学习的方法应该更鲁棒，而不是用固定的策略来区分）。anyway， div v 是可以计算的已知量；

因为需要保持边界一致，边界条件上像素值等于背景图片即可。当然也可以做一些策略，但同样也可以计算得到的已知量。

现在很轻松了，边界条件已知、散度已知，在离散空间中求解泊松方程中的  ，参考上一节的求解过程即可。

 

代码实现

 

函数代码已经收录在了 OpenCV 的官方函数 seamlessClone 里：github source code

使用的时候，需要三张图片：前景图、背景图、mask图（指明前景图中需要融合的区域，最简单的就是直接等于前景图大小的 mask，待融合区域是白色，其余位置黑色）。

下面我们使用 OpenCV 的 Python 接口来动手试试，用到以下两张图以及一段代码：

 

 

 

import cv2
import numpy as np


# Read images : src image will be cloned into dst
dst = cv2.imread("background.jpg")
obj= cv2.imread("foreground.jpg")


# Create an all white mask
mask = 255 * np.ones(obj.shape, obj.dtype)


# The location of the center of the src in the dst
width, height, channels = dst.shape
center = (height/2, width/2)


# Seamlessly clone src into dst and put the results in output
normal_clone = cv2.seamlessClone(obj, dst, mask, center, cv2.NORMAL_CLONE)
mixed_clone = cv2.seamlessClone(obj, dst, mask, center, cv2.MIXED_CLONE)


# Write results
cv2.imwrite("images/opencv-normal-clone-example.jpg", normal_clone)
cv2.imwrite("images/opencv-mixed-clone-example.jpg", mixed_clone)

 

最终效果如下：

 

 

 

---

审核编辑 ：李倩