浅析模数转换器的基本原理

随着集成电路技术的快速发展以及工艺制程的不断进步，数字电路处理信息的能力愈发强大。数字信号由0和1高低电平组成，易于存储，噪声容限低且抗干扰能力强，在数字域中进行信号处理具有速度快、精度高以及成本低等优势。

在现实生活中，自然存在的信号，如声音、温度、图像、重量等都是模拟信号，所以必须通过模数转换器（Analog-to-Digital Converter，ADC）将模拟信号转换成数字信号，在经过数字信号处理（Digital Signal Processing，DSP）后，由数模转换器（Digital-to-Analog Converter，DAC）将数字信号转换成可被人们感知的模拟信号，系统处理流程如图所示。

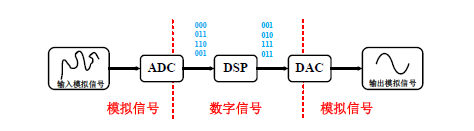
因此，ADC和DAC作为连接数字域和模拟域之间的桥梁，是不可或缺的部分，其性能往往决定整个系统的性能上限，重要程度不言而喻。

2

ADC分类

按照采样频率的不同，ADC大致可以分为两类：Nyquist ADC和过采样ADC。Nyquist ADC的采样频率略大于或者等于Nyquist频率，包括的种类较多，其中具体性能表现各有差异：

快闪型（Flash）ADC的转换速率最快，但分辨率最低，而且体积、功耗较大，所以目前应用不太普遍；逐次逼近型（Successive Approximation，SAR）ADC突出特点是功耗低，但其转换速度和精度处于中等水平；流水线型（Pipeline）ADC的转换速度很快，但同时牺牲了分辨率，所能实现的精度也处于中等水平；其余还有积分型ADC、单斜坡ADC等。

Nyquist ADC在高速信号测量领域具有良好表现，但由于器件匹配误差以及电路中存在的非理想性等因素，实现的精度不高，一般在14位以下。过采样ADC的采样频率远高于Nyquist频率，以Sigma-Delta ADC为代表的过采样ADC明显地降低了系统对模拟器件工作电压和工艺匹配精度的要求，同时对模拟器件的需求数量进一步下降，不需要复杂的采样保持电路和比较网络等。

3

ADC基本原理

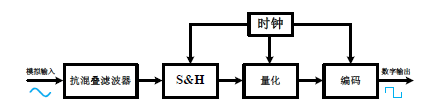
ADC是一种将在时间和幅度上都连续的模拟信号转换成时间上离散、幅度上量化的数字信号的电子元件，包括采样、保持、量化及编码等一系列过程，如图所示。

首先，输入信号经过一个抗混叠滤波器（Anti-Alias Filter，AAF）来滤除信号带宽外的干扰信号；其次，采样保持电路将某个时刻的输入信号采样并保持固定时长，替代该段时长内的输入信号值，在时间上将模拟信号离散化；然后，量化器将采样保持电路中的时间离散信号在幅度上近似到有限个预先设定的固定幅值，即在幅度上将输入信号离散化；最后，每个固定幅值都对应一个数字输出码，可以根据需要对数字信号编码，用于后续的运算处理，采样、量化和编码一般是在时钟控制下完成的。

采样与量化

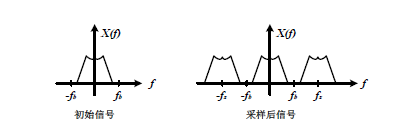
对模拟输入信号进行周期性的采样，能得到时间上离散的输入信号序列，即x(s)=x(nTs)。其中，x(s)为模拟输入信号，Ts=1/fs，Ts为采样周期，fs为采样频率。根据Nyquist采样定理，当fs和信号带宽fb满足fs≥2fb时，采样后的信号就不会发生频谱混叠，能够进行信号重建。信号采样前后的频谱如图所示。

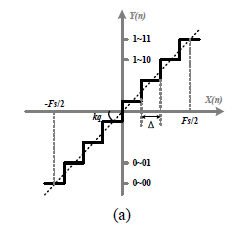
将采样后的信号在幅值上按一定间隔进行离散化的过程叫做量化，图（a）为多位量化器的输入输出曲线。其中，kq为量化器转换曲线的斜率，Fs（Fullscale）表示量化器的满量程输入，输入信号的范围为[-Fs/2，Fs/2]，对应的数字输出从全0到全1。输出数字信号的位数N可以表示量化器的精度，即量化器可以分辨出的最小步长Δ=Fs/(2N-1)，Δ也被称为最低有效位（Least Significant Bit，LSB）。由于量化器位数有限，数字输出信号对应的电平值不能准确表示输入信号，两者之间的差值称为量化误差，也叫量化噪声，用e(n)表示。以每个间隔的中点来确定对应的数字码区间，e(n)的幅度范围为[-Δ/2，Δ/2]，如图（b）所示。

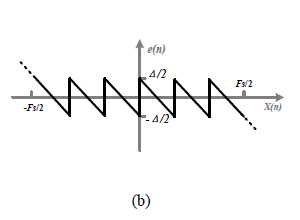
若输入信号的幅度超过量化范围，对应的量化误差也会超出Δ/2，导致量化器过载，量化器的输入输出关系如式:

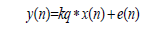
当量化器工作时，只要输入信号幅度在[-Fs/2，Fs/2]内，产生的量化误差同样只在[-Δ/2，Δ/2]范围内随机变化，并且量化器位数越高，量化误差越小。假设输入信号在量化范围内幅值随机变化，量化误差则可以等效为随机的白噪声，并且在[-Δ/2，Δ/2]范围内均匀分布，量化误差的能量可以表示为：

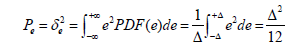
因此，量化噪声的能量谱密度可以由式表示:

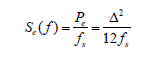
从上式可以看出，提高采样频率可以降低量化噪声的能量谱密度。过采样ADC通过提高采样频率，降低信号带宽内的量化噪声能量，从而提高信噪比。