卡尔曼或FIR滤波器适用于我的IMU

Ian Beavers

这些过滤器选项中的每一个在 IMU 中都提供了截然不同的功能。在大多数情况下，它们在操作中是独立的。它们的使用将取决于终端系统的要求。让我们进一步了解一下细节以及它们如何应用于传感器系统。

将抽取与有限脉冲响应（FIR）滤波器结合使用是一种降低IMU全输入带宽的方法，以便仅关注狭窄的低通活动频带。当系统受到许多旋转和加速度频率运动时，这尤其有用，其中只有一部分在传感器内需要观察。此外，任何不必要或被忽略的高频活动都有可能混叠回目标频带，而不会受到FIR带通滤波器的滤波抑制。

当不需要传感器的全部带宽时，FIR滤波器最有价值。相反，如果对低通区域内的已知信号频率带宽感兴趣，则可以滤除不需要的信号。例如，系统的目标旋转频率可能仅在 20 Hz 到 50 Hz 之间。虽然可能还有其他更高频率的噪声可以检测到，但在IMU内进行测量并不重要。图1显示了使用抽取和FIR滤波器选项B将全带宽进行低通滤波16倍的方法。

 

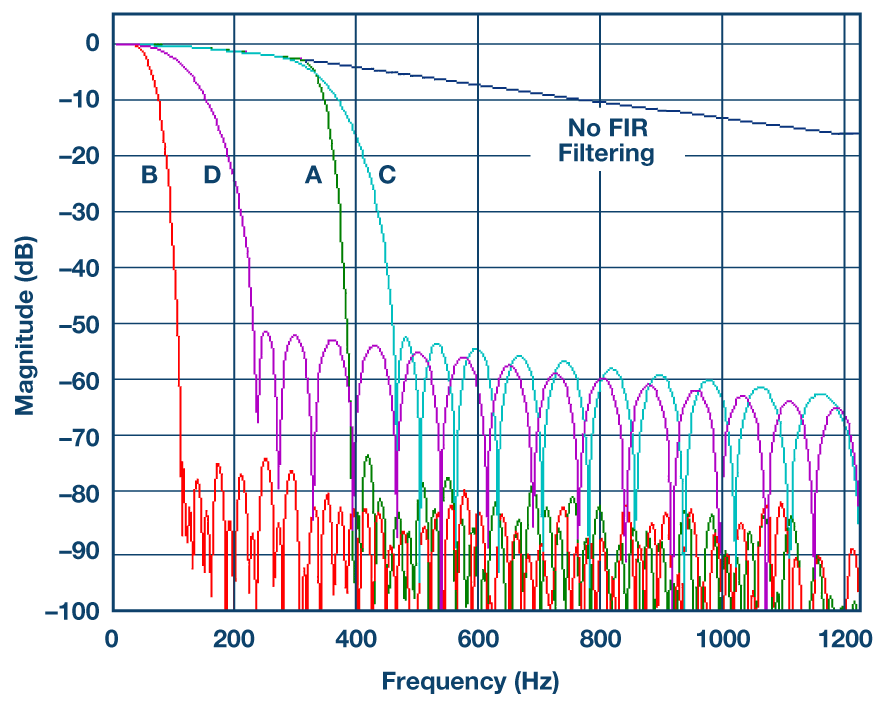
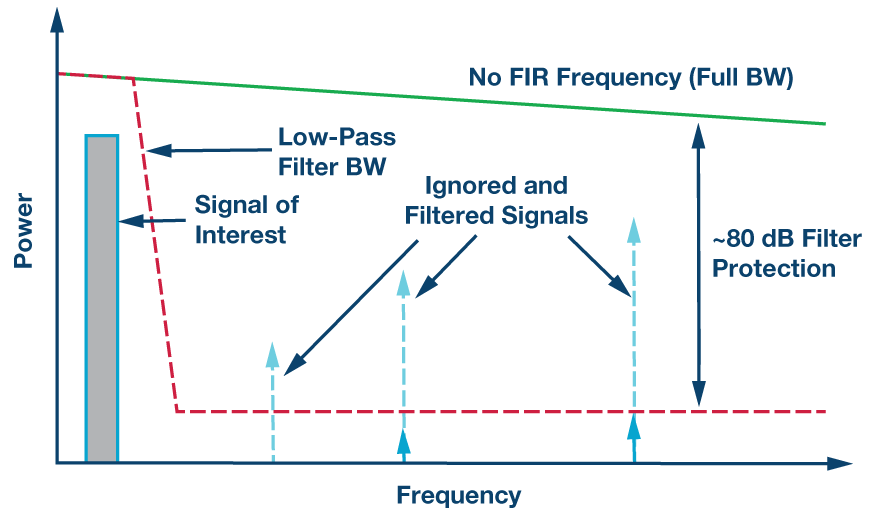
图1.ADIS16480的FIR滤波器响应（左）和B滤波器的示例用例（右），其中可以滤除不需要的信号以聚焦在目标的低通频率带宽内。

卡尔曼滤波器以电气工程师共同发明人鲁道夫·卡尔曼的名字命名，与抽取滤波器和FIR滤波器组合相比，具有不同的优势。描述卡尔曼滤波器的“滤波器”一词实际上可能有点用词不当。它更类似于“递归估计器”。卡尔曼滤波器在系统中最有价值，在这些系统中，预测位置可能比可能具有位置误差的未滤波噪声解更有用。卡尔曼滤波器使用 IMU 内的所有传感器轴贡献来估计方向角。

虽然比单个方程复杂得多，但我们可以通过删除状态矩阵来简化这里的用例，我们可以得到如下所示的数学：

Xk= Kk×Zk+ （1 – Kk） × XK–1

Xk= 电流估计

Kk= 卡尔曼增益

Zk= 测量值

XK–1= 先前的估计

我们可以对待每一个k作为识别每个传感器轴输出的离散时间间隔或样本。新的最佳估计是从之前的最佳估计值做出的预测，加上已知外部影响的增益校正权重。初始卡尔曼增益或协方差系数在IMU寄存器设置中使用，以建立Isensor输出矢量之间的预期相关性。在 IMU 中使用的最佳协方差值通常取决于特定的观测值。因此，它可以是测量、观察数据、分析、调整和重复的迭代过程。ADIS16480采用内部算法，使用创新残差，可以实时自适应地调整协方差项。

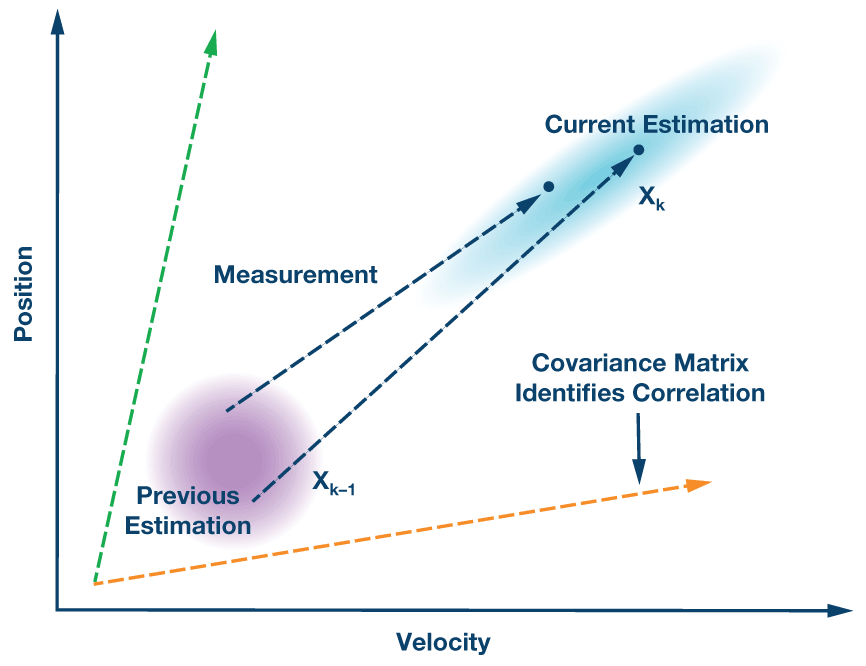
图2.一个示例卡尔曼滤波模型，其中两个变量（在本例中为速度和位置）具有一定程度的相关性。当前位置可以根据前一个位置、IMU 测量的加速度值以及两者之间相关性的协方差权重来估计。

审核编辑：郭婷