

Wolfram语言与Mathematica 13.2 版本(4)
描述
显著加快多项式运算速度
几乎任何代数计算最终都会以某种方式涉及多项式。多项式从一开始就是Mathematica 和Wolfram语言中优化的部分。事实上,在超过四分之一个世纪的时间里,我们对它们进行的基本操作几乎不需要更新。但是现在在版本13.2中——由于新的算法和新的数据结构,以及使用现代计算机硬件的新方法——我们正在更新一些核心多项式运算,并使它们大大加快。顺便说一下,我们也得到了一些新的多项式函数。
这是两个多项式的乘积,展开:
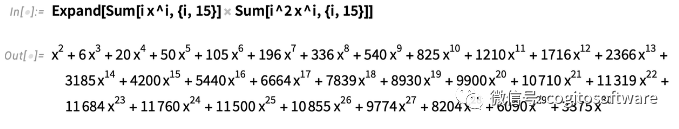
像这样的分解多项式几乎是即时的,并且从版本1 开始就一直如此:
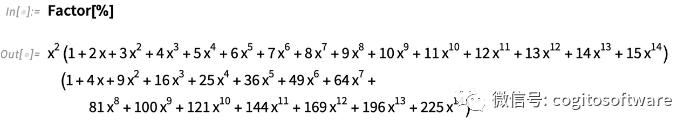
但是现在让我们把它做得更大:
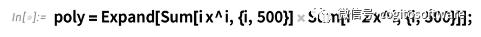
展开多项式中有999 项:

分解这不是一个简单的计算,在版本13.1 中大约需要19 秒:

但是现在,在版本13.2 中,同样的计算需要0.3 秒,快了近60 倍:
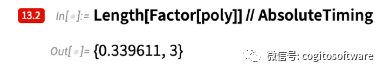
很少有任何东西能提高60倍。但这是其中一种情况,事实上,对于更大的多项式,该比率将进一步稳步增加。但这仅仅是只与晦涩的大多项式有关的东西吗?嗯,没有。尤其是因为事实证明,大多项式出现在各种重要地方的“引擎盖下”。例如,看似无害的物体
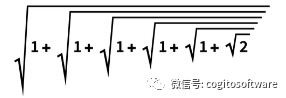
可以作为代数数进行操作,但多项式最小:
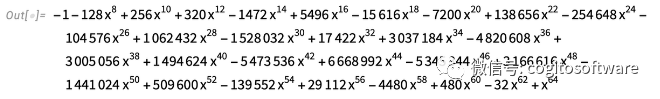
除了分解之外,版本13.2还显著提高了多项式结果、GCD、判别式等的效率。所有这些都使得对多项式线性代数的变革性更新成为可能,即对元素为(单变量)多项式的矩阵的操作。
下面是一个多项式矩阵:
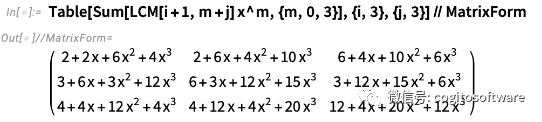
这是矩阵的力量:
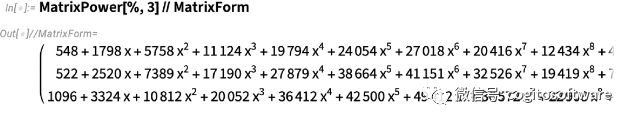
而这个的决定因素:
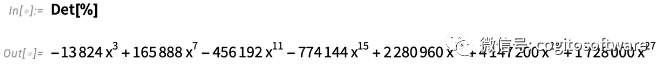
在13.1 版中,这看起来并不那么好;结果未展开,如下所示:
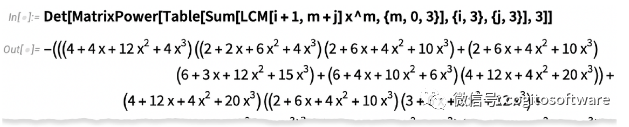
在版本13.2 中,大小和速度都得到了显著改进。这是一个更大的案例- 在 13.1中计算需要一个多小时,结果的叶子数量惊人地达到178 亿


多项式线性代数在“幕后”用于许多领域,特别是在处理线性微分方程、差分方程及其符号解时。在13.2版本中,不仅多项式MatrixPower和Det,而且LinearSolve,Inverse,RowReduce,MatrixRank和NullSpace都得到了显着的加速。
除了显著的速度改进之外,版本13.2 还增加了一个多项式功能,我碰巧已经等待了30 多年:有限域上的多元多项式分解:
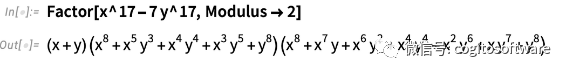
事实上,查看我们的档案,我发现许多请求至少可以追溯到1990 年——来自相当多的人——要求这种能力,尽管1991 年的内部说明很有魅力地指出:

是的,没错。但是31 年后,在13.2 版中,它完成了!
审核编辑 :李倩
-
如何优化 Mathematica 代码性能2024-12-26 1814
-
特斯拉FSD V13.2版本正式发布2024-12-03 1562
-
Wolfram应用服务器2023-03-23 942
-
Wolfram应用服务器的优势及其主要特点2023-03-22 1061
-
Wolfram语言与Mathematica 13.2 版本(7)2023-02-24 940
-
Wolfram语言与Mathematica 13.2 版本(6)2023-02-21 961
-
Wolfram语言与Mathematica 13.2版本(2)2023-02-13 1007
-
Wolfram语言与Mathematica13.1版本2022-11-11 1349
-
关于Wolfram语言与Mathematica13.1版本上线2022-10-28 1212
-
Wolfram语言与Mathematica13.1版本上线2022-10-21 1928
-
iOS13.2版本用起来怎么样2019-10-30 6513
-
Mathematica是什么?Mathematica怎样使用?Mathematica教程免费下载2018-09-13 1347
-
在树莓派上用Wolfram语言拍照2016-01-26 5587
-
Mathematica入门教程之Mathematica的基本语法特征2011-02-18 14485
全部0条评论

快来发表一下你的评论吧 !

