模数转换器的术语及采样量化编码

一、模数转换器

• 模拟信号(Analog Signal) ：用连续变化的物理量来表示信息。自然界中大部分信号都是模拟信号，比如：温度、湿度、声音等。在工程上，我们使用传感器将物理量转化为电信号。在一定范围内，取值是连续的。
• 数字信号(Digital Signal) :使用有限且离散的数值表示信息。
• ADC(Analog-to-Digital Converter) ：将模拟信号转化为数字信号的设备。

为什么要将模拟信号转化为数字信号？

1. 数字信号抗干扰能力强，适合长距离传输；(无线通信)
2. 数字信号存储效率高；
3. 数字信号易于处理，已经发展出很多高级的数字信号处理算法，堪称潜力无限；
4. 现代计算机的核心都是数字系统，便于数据交互；

二、ADC 术语

• 转换位数(分辨率),就是用多少位二进制数表示最大的模拟信号，用N表示；
• 参考电压，就是最大的模拟信号表示的电压值，用Vref表示；
• 满量程范围，就是最大值和最小值的差，如果是正弦波的话，就是Vpp，用FSR表示；
• 量化电平，模拟信号的分辨率,用Q表示；

三、数学基础

此部分补充一点关于概率论的知识，后续推导能用到，如果熟悉此部分可以跳过；

首先来介绍几个关键的概念。

• 概率密度函数(Probality Density Function,PDF)

随机变量X是连续随机变量，才能定义PDF，随机变量在区间[a,b]上的概率

上式中,称为 概率密度函数 ，那么,并且,下文中用PDF(X)来表示概率密度函数。

如果X是离散随机变量，那么只能定义分布律，

• 累计分布函数(Cumulative Distribution Function,CDF)

那么，对于连续型随机变量X

• 数学期望(Mean)

为了方便理解，先介绍离散型的随机变量X的数学期望，用符号E(X)表示；假设分布律,那么

对于连续型随机变量X，其数学期望是：

数学期望的本质是加权平均数

• 方差(Variance)

用于表征随机变量离群特征。数学上，计算变量与均值的偏差。

对于离散型随机变量X，方差定义为：

对于连续型随机变量X，方差定义为：

综上，

四、采样量化编码

4.1 采样

假设模拟信号,使用冲击采样，采样间隔T，如下图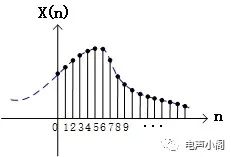：那么，

假设模拟信号带宽为2B，为了简单理解就不上傅里叶变换了，直接来个图：模拟信号经过采样后，在频域上做周期性延拓。根据奈奎斯特（Nyquist）采样定理：采样频率至少大于2倍的信号带宽

此部分不是文本重点，不再详细推导理论。

4.2 量化与编码

此部分主要关注量化噪声，在这之前先说说量化误差。我们知道模拟信号是连续的，而数字信号是有限个离散值，因此必然引入误差，误差定义为：实际值与量化值的差值，用符号e表示。一般量化方法有舍入法和 截断法 。本文只介绍舍入法，可以证明这两种方法可以得到相同的结论。以下示例中N = 3

可以看出:舍入法量化误差范围(-Q/2,+Q/2)

为了分析量化误差数学特性，做出以下假设：

1. 误差在区间(-Q/2,+Q/2)中均匀分布；
2. 误差序列服从高斯白噪声；
3. 误差序列与信号序列不相关；

那么误差e概率密度函数为：

误差的数学期望：

误差的方差：

以dB表示的信噪比(Signal to Noise Ratio):

上式中，：信号功率；：噪声功率

那么，

假设信号为,那么E[f(t)] = 0,信号方差：

信噪比可以化简为：

上式说明了量化位数与信噪比的关系，我们常用的量化位数有：8bit，12bit，14bit，16bit，24bit,32bit,那么对应的信噪比如下表：

量化位数/bit	信噪比/dB
8	49.93
12	74.01
14	86.05
16	98.09
24	146.26
32	194.42

五、鸣谢！

本文排版采用了Markdown Nice