

解析LeetCode第226号题目:反转二叉树
电子说
1.4w人已加入
描述
今天给大家讲解一道微软一面的算法题,也是LeetCode第226号题目,反转二叉树,就像这样:
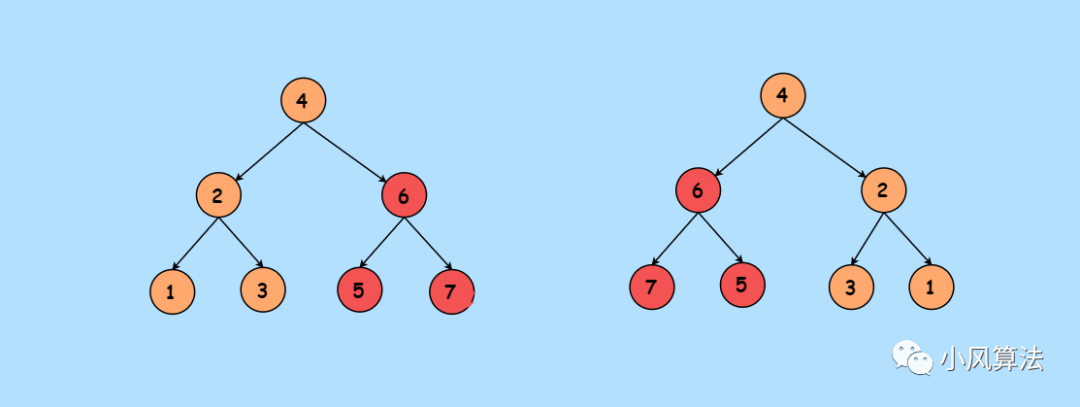
简单讲就是把每个节点的左子树和右子树进行交换 。
显然,这需要我们能够遍历该二叉树。
那么遍历二叉树就有两种经典的解法:深度优先遍历,Deep First Search,简称DFS;另一个是广度优先遍历,Breadth First Search,简称BFS。
深度优先搜索
顾名思义,深度优先搜索是我总是优先访问“ 节点的子节点的子节点 。。”,这是什么意思呢?对于给定的二叉树,我们首先访问节点4:

接下来访问4的左子树2:

再接下来依然访问2的左子树1:

1是叶子节点,其左右子树都为空,因此返回上一个节点2,然后访问其右子树3,重复上述过程直到所有节点访问完毕。
你会发现,这其实是一个递归过程:

深度优先搜索非常适合用递归代码编写。
回到这个题目,代码就可以这样写:
TreeNode* invertTree(TreeNode* root) {
// 如果是空节点,直接访问
if (root == nullptr) return nullptr;
// 找到当前节点的左右字节点,并交换
auto* left = root->left;
auto* right = root->right;
root->left = right;
root->right = left;
// 处理当前节点的左右子节点
invertTree(left);
invertTree(right);
return root;
}
接下来我们看广度优先搜索。
广度优先搜索
个人认为广度优先搜索相对来说更容易理解,通俗的讲,广度优先搜索是“ 先把同辈访问完再访问下一辈 ”,因此这一种“ 层级 ”遍历方法,先是访问第一层,然后是第二层。。直到最后一层,就像这样:

在这里我们可以使用一个队列,先把根节点4放入队列中,然后从队列依次取出节点,交换其左右字数,并将该节点的左右字数也放到队列中,重复上述过程直到队列为空,用代码就是这样实现:
TreeNode* invertTree(TreeNode* root) {
if (root == nullptr) return nullptr;
// 定义队列,并把根节点放到队列中
queue q;
q.push(root);
while(!q.empty()) {
// 从队列中取出节点
auto* t = q.front();
q.pop();
// 交换该节点的左右子树
auto* left = t->left;
auto* right = t->right;
t->left = right;
t->right = left;
// 如果该节点的左右子树不空则放到队列
if (left) q.push(left);
if (right) q.push(right);
}
return root;
}
广度优先搜索与深度优先搜索不仅仅可以用在二叉树中,这两种遍历方法有着极其广泛的用途,当我们积攒足够多的使用案例后将会系统总结这两种遍历方法。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
这么简单的二叉树算法都不会?2023-08-29 1364
-
二叉树的代码实现2023-01-18 1722
-
C++构建并复制二叉树2023-01-10 1554
-
使用C语言代码实现平衡二叉树2022-09-21 1713
-
怎么就能构造成二叉树呢?2022-07-14 2142
-
C语言数据结构:什么是二叉树?2022-04-21 4313
-
如何才能够翻转二叉树2021-09-01 2113
-
二叉树的前序遍历非递归实现2021-05-28 2414
-
二叉树操作的相关知识和代码详解2020-12-12 2493
-
详解电源二叉树到底是什么2019-06-06 11207
-
关于二叉树一些数据结构和算法相关的题目2018-02-07 3558
-
二叉树层次遍历算法的验证2017-11-28 2342
-
计算机二级二叉树的问题2012-09-04 4236
-
基于二叉树的时序电路测试序列设计2012-07-12 1001
全部0条评论

快来发表一下你的评论吧 !

