失配损耗对射频功率测量和级联放大器增益的影响是什么

使用失配损耗方程，了解失配损耗对射频功率测量和级联放大器增益的影响。

有效的功率传输是射频设计中的一个主要问题。由于阻抗不连续性可以反射电波，它们会导致功率损耗，通常称为失配损耗 (ML)，这在各种应用中都有体现。例如，射频功率传感器测量的功率，以及射频模块级联的有效增益，都会受到波反射的影响。对于级联的 RF 块，我们的目标是尽量减少失配损失，以便我们可以传输尽可能多的功率。此外，通过最小化失配损失并为此错误开发适当的统计模型，我们可以估计系统中的不确定性。

在本文中，我们将首先研究失配损失方程。然后，我们将讨论这种现象对射频功率测量和级联放大器有效增益的影响。

失配损失：两种不同的定义

考虑图 1 中的图表，该图表显示了在输入和输出端口连接到不匹配阻抗（Z s  ≠ Z 0 和 Z L  ≠ Z 0 ）的传输线。

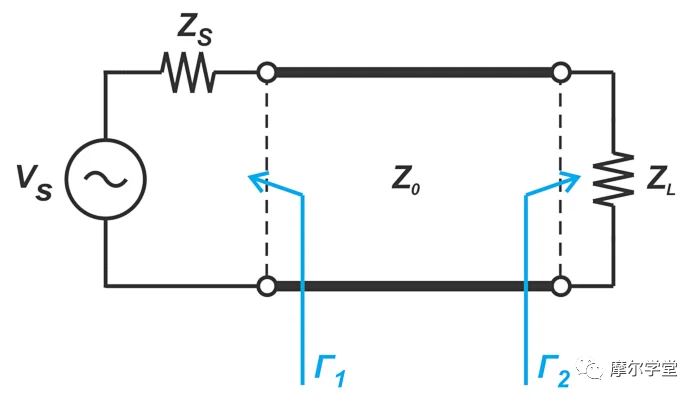
图 1. 示例图显示了在输入和输出端口连接到不匹配阻抗的传输线。

公式 1 显示了一种定义上述电路失配损耗的方法： 

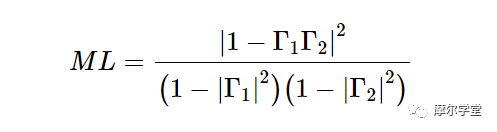
等式 1。

这个等式在之前的文章中进行了非常详细的研究，它给出了相对于电源可用功率的功率损耗。例如，如果源传送到共轭匹配负载的功率为 -30 dBW，而实际负载的 ML 为 1 dB，则传送到负载的功率为 -31 dBW。

根据上述定义，参考功率是可从源获得的功率。通常使用另一个（实际上更有用的）参考功率来定义失配损耗；源传送到 Z 0 终端的功率（其中 Z 0 是线路的特性阻抗，50 Ω 是标准值）。

考虑到这一点，您可能想知道为什么我们对可以传输到 Z 0 终端的功率感兴趣。在 RF 系统中，大多数电路的设计都假设它们将与某些已知的特性阻抗一起使用。换句话说，在正常操作期间，假定大多数电路都具有 Z 0 源电阻和 Z 0 负载电阻。这就是为什么 RF 块通常在这些条件下进行表征的原因。为了更好地理解此功能，请考虑测量双端口网络 S 参数的测试设置（图 2）。

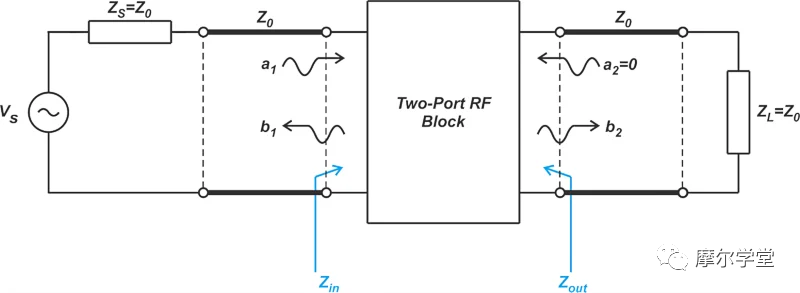
图 2. 为测量双端口网络的 S 参数而设置的示例图。

对于 S 参数测量，一个端口由串联电阻为 Z 0的源驱动， 另一个端口以 Z 0 负载端接。使用上图，我们可以测量输入反射系数 (S 11 ) 和从端口 1 到端口 2 的传输系数 (S 21 )。

请注意，输出端口的 Z 0 终端可确保没有能量从负载反射 (a 2  = 0)，因此，b 1 和 b 2 仅作为入射到输入端的行波的结果产生端口（a 1）。还值得一提的是，网络输出阻抗 Z out 不必等于 Z 0。事实上，Z out  = Z 0很少见。我们只需要有 Z L  = Z 0 来确保 a 2 = 0。根据定义，S 参数基于使用匹配终端的测试设置。与其他类型的双端口网络表示（例如 T 参数）相比，这显着简化了 S 参数的测量。  

由于 RF 模块的响应通常在 Z 0 环境中表征（Z S  = Z L  = Z 0  ，其中 Z 0  = 50 Ω 是标准值），因此需要找到与功率相关的失配损耗源传送到 Z 0 终端。 

匹配负载警告

对于图 1 中的电路，通用术语“匹配负载”可以指代两种不同的条件：�大号=�小号＊ Z L  = Z 0。第一个条件对应于最大功率传输定理，而第二个条件给出了无反射负载。使用术语匹配负载有时会引起混淆。为了更清楚，我们可以使用术语“共轭匹配”来指代�大号=�小号＊和术语“Z 0 匹配”或“无反射匹配”来描述 Z L  = Z 0。  

失配损耗 WRT 功率传输到 Z 0 终端

考虑图 1 中的图表，可以看出 失配损耗 (ML) 相对于可提供给负载阻抗 Z 0的最大功率 的计算公式如下： 

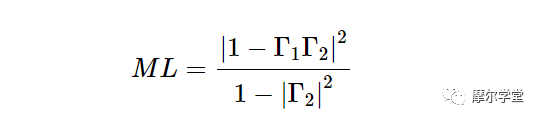
等式 2。

请注意，Γ 1 和Γ 2 分别表示线路源端和负载端的反射系数。ML 如公式 2 所示定义，传输到 Z 0终端的功率 (P Z0 ) 和传输到任意负载的功率 (P Load ) 与以下公式相关：

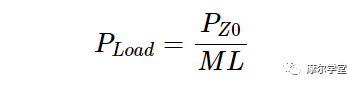
等式 3。

我们也可以用分贝表示上述等式。在许多应用中，Γ 1 和Γ 2的相位角 是未知的；并且我们只能找到 ML 的上限和下限来确定功率传输不确定性的范围。ML 的最大值和最小值之间的差异，称为失配不确定性 (MU)，由下式给出：

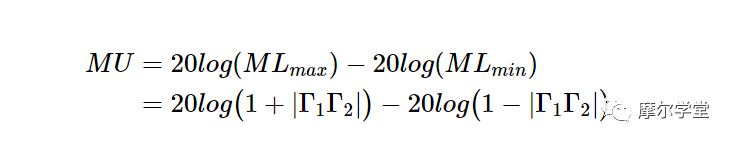
等式 4。

在上一篇文章中，我们使用方程式 1 而不是方程式 2 推导出了相同的方程式。虽然方程式 1 和 2 给出了关于两个不同参考功率的功率损耗，但正如预期的那样，它们会导致相同的失配不确定性项。让我们看一个示例，了解如何在功率传感器应用中使用上述方程式。

示例 1：RF 功率传感器

顾名思义，功率传感器用于测量射频和微波信号的功率（图 3）。  

图 3.连接到脉冲功率传感器的 R&S NRX 功率计。图片由罗德与施瓦茨提供

理想情况下，传感器应测量传送到传感器的净功率。实际情况并非如此，因为一些净输入功率可能不会在传感元件中耗散。例如，辐射造成的损失可能会引导能量远离传感元件。因此，最终由传感器 P m测量和指示的功率与传递给传感器的净功率 P Load 并不完全相同。测试设备制造商使用一些校准系数来描述这两个量之间的关系：

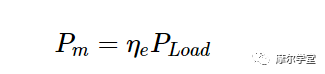
等式 5。

在上式中，η e 称为“有效效率”。在表征发电机时，所需量通常是 Z 0负载中耗散的功率， 而不是功率传感器输入阻抗中耗散的功率。将方程式 2 和 3 代入方程式 4 可得出 P Z0的方程式：

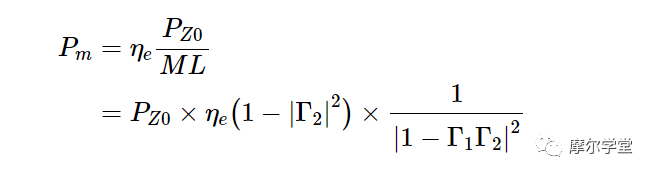
等式 6。

因子 (eta _e ig (1-|Gamma_2|^2)) 称为校准因子 K b。大多数现代功率计都能够消除校准因数中的误差。使用此功能时，公式 5 可改写为：��(1−|Γ2|2)称为校准系数 K

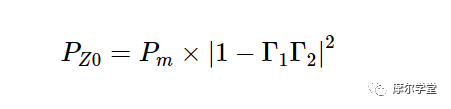
请注意，误差项实际上与上面讨论的失配不确定性 (MU) 有关。例如，如果 (| Gamma_1 |) ≤ 0.09 且 (| Gamma_2 |) ≤ 0.2，则误差的最大值和最小值是：

|Γ1| ≤ 0.09 和|Γ2|≤ 0.2，误差的最大值和最小值分别为：

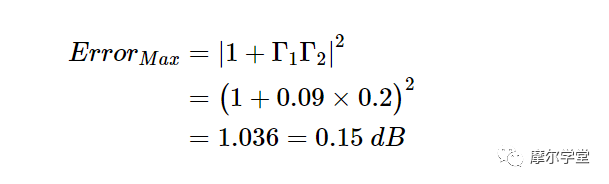
和 

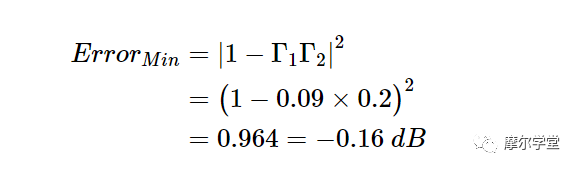
因此，P Z0的实际值 可比功率计指示值高0.15 dB或低0.16 dB。 

示例 2：级联块的有效增益

考虑图 4 中所示的配置。

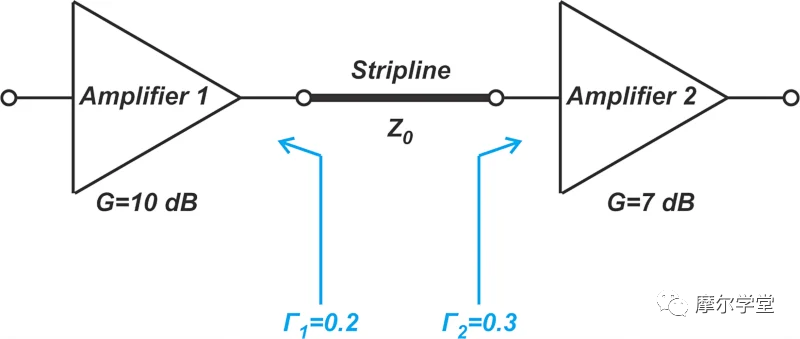
图 4. 通过带状线连接的放大器配置示例。

在本例中，放大器 1 和 2 的传感器增益分别为 10 dB 和 7 dB。由于带状线两端的阻抗不匹配，放大器1提供的部分能量在两个阻抗不连续点之间来回反弹。可以证明，这些波反射导致功率损耗，由下式给出：

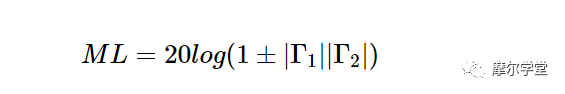
等式 7。

您可以在WF Egan 的《实用射频系统设计》第 2 章中找到该等式的证明。例如，如果 (| Gamma_1 |) ≤ 0.2 且 (| Gamma_2 |) ≤ 0.3，则失配引起的损耗的最大值和最小值分别为 0.51 dB 和 -0.54 dB。0.54 dB 的负损耗实际上代表额外的功率增益。现在我们可以找到级联的有效增益。通常，我们期望上述电路的增益为10+7 = 17 dB；然而，由于失配损耗，实际增益可能在 17 - 0.51 = 16.49 dB 和 17 + 0.54 = 17.54 dB 之间变化。|Γ1| ≤ 0.2 和|Γ2| ≤ 0.3，失配引起的损耗的最大值和最小值分别为 0.51 dB 和 -0.54 dB。0.54 dB 的负损耗实际上代表额外的功率增益。现在我们可以找到级联的有效增益。通常，我们期望上述电路的增益为10+7 = 17 dB；然而，由于失配损耗，实际增益可能在 17 - 0.51 = 16.49 dB 和 17 + 0.54 = 17.54 dB 之间变化。

射频功率传输设计中的失配损耗和阻抗

阻抗不连续性使我们无法在 RF 设计中进行有效的功率传输。这表现为功率损耗，并导致各种应用中的不确定性。在本文中，我们讨论了射频功率传感器测量的功率和级联放大器的有效增益受失配损耗的影响。

审核编辑：陈陈