

怎么设计模拟无源滤波器-1
模拟技术
描述
相信做硬件的朋友对模拟滤波器设计并不陌生,给出一个规格指标,都可以依据滤波器设计软件就可以设计出符合设计要求的滤波器。但是模拟滤波器参数是如何确定的?假设我们要一个线性衰减的滤波器该如何设计?假如我们要实现一个滤波器设计软件应该掌握哪些知识?
前言
本期目标是设计一个模拟无源滤波器综合和仿真软件,并且集成在小程序中。
除了常用滤波器外,最终目标是实现特定形状的频率响应曲线,如线性衰减补偿曲线,并且可以使用实际元器件实现。另外一旦掌握了滤波器设计方法,那么我们可以更进一步,将实际器件模型考虑进去,从而可以自动设计更为接近实际频率响应的滤波器。
要实现上述目标是有挑战的,其中之一就是如何依据频率响应来求复数域的传输曲线,然后由传输函数求取特定网络的具体数值。
所以这里将此事情分为如下步骤进行:
- 掌握阶梯网络综合方法
- 实现滤波器电路仿真(mini js无源电路仿真引擎)
- 实现巴特沃斯滤波器设计(由传输函数得到实际元器件值)
- 搭建起小程序基本程序框架(发布第一实用版本)
- 实现切比雪夫,贝塞尔,椭圆滤波器设计
- 实现不同衰减类型的滤波器设计(LPF,BPF,HPF,BRF)
- 实现线性衰减补偿滤波器设计
- 实际电路参数设计和优化
- 全通滤波器,移相网络实现
模拟无源滤波器发展史
滤波器的历史最早可以追溯到1890年代,当时有线电话被发明并广泛应用,远距离空中架设通讯线缆的需求非常迫切,但是人们发现当电话线缆长度增加后线路损耗迅速增加,导致语音出现严重失真。解决办法正是“Pupin线圈/加载线圈”发明人普平(Mihajlo Pupin, 1858.10-1935.3)于1899年所提出的增加线路电感的办法,即每隔一段距离增加一个电感从而改善电话传输质量。

若站在上帝视角看待当时的问题就是传输语音信号的双绞线寄生电容太大,阻抗非常低,导致驱动电话线驱动能力不足,整个电路相当于一个巨大的RC滤波器,信号迅速衰减,当在线缆中插入Pupin线圈,情况就不同了,整个网络阻抗变高,源可以很容易的驱动整个网络,带宽变高,通话质量得到大幅改善,据文献介绍性能可提升6000倍。这项技术也因此让Pupin名利双收 。
赫维赛德(Oliver Heaviside,1850.3-1925.2),对,就是那个将20多个麦克斯韦的方程组改为4个方程组的神人,1876年他提出并推导了电报方程(也就是将传输线划分为小段的RLC梯形网络结构 ),并且使用了微分算子用来计算电路,通过计算提出了需要在传输线上加电感来减小失真,但是这个增加电感的想法由于种种原因并没有得到实施,也没有申请专利,他在传输线上增加电感这一骚操作要比普平的早7年,这也为后续AT&T关于加载电感的专利之争埋下了伏笔。赫维赛德可能脾气比较古怪,AT&T公司本来给他抛出橄榄枝要收了他的专利并且给他一大笔钱,但是被他拒绝了,赫维赛德一生贫穷,即使在晚年他还需要靠亲戚的救济来维持生活。

坎贝尔(George Ashley Campbell, 1870.11-1954.11)在AT&T工作,并继续研究Pupin线,并且一直挑战Pupin的专利(要知道AT&T是购买了pupin的专利权,但是由于赫维赛德的文章是在Pupin申请之前所发表,所以按美国专利法实际Pupin的专利是无效的,关于加载电感是有一段权利之争的,详见 ),并且完善Pupin线的理论,在工作中他发现Pupin线有一个非常陡峭的截止频率,并且可以用这个特性来滤除信号的谐波,这里他已经将加载线当成了滤波器来使用了。但是一个问题是到底每隔多少距离就插入一个多大的电感能让传输距离达到最远。1910年坎贝尔就发明了镜像法来计算滤波器参数的方法,并且在商业上取得了成功。这个时期的研究拉开了滤波器设计的序幕,并且很多概念到现在还在使用,比如使用了梯形网络(ladder network),不同的滤波器类型:低通滤波器、高通滤波器、带通滤波器、带阻滤波器 。
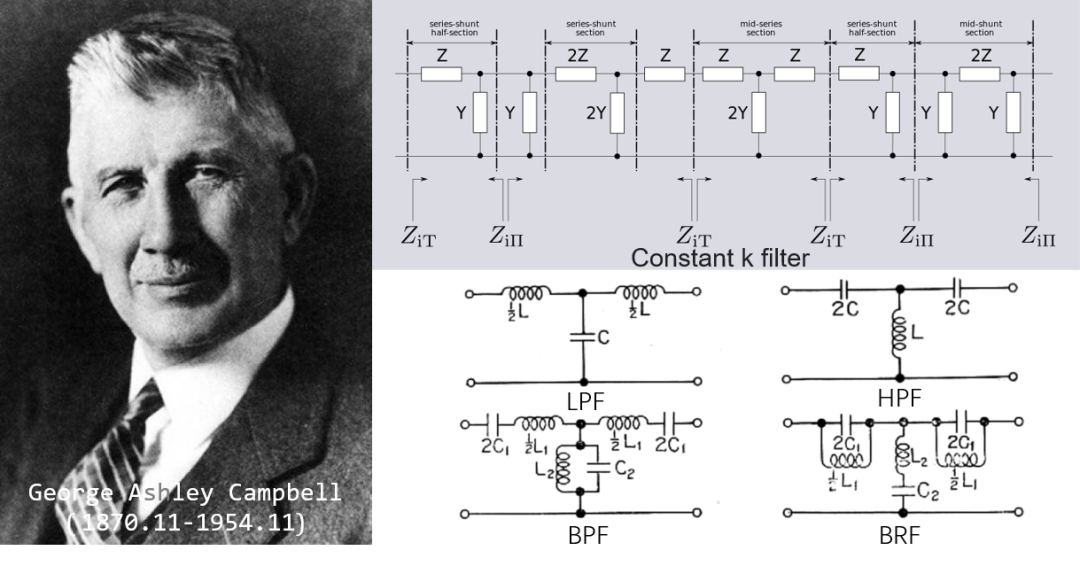
坎贝尔的滤波器设计方法也叫定k滤波器(Constant k filter),这种滤波器也是最简单的滤波器,滤波器就是一个传输线的等效,是由相同的T型或PI型节组成,其中的k表示传输线的特征阻抗,定k表示组成这个滤波器节处的阻抗处处相等 。
佐贝尔(Otto Julius Zobel, 1887.10-1970.1)发展了滤波器的设计方法,他也是在AT&T工作,1920年发现了坎贝尔的滤波器具有恒定阻抗特性 ,并且发明了m推演型滤波器(m-derived filter),这种滤波器和定k滤波器一样可以使用了镜像法分析 ,这个滤波器引入了一个参数m,不同参数滤波器特性会不同,在1923年佐贝尔对之前结果进行了系统理论分析,这种分析方法是从中间节点(mid-shunt)的阻抗和定k阻抗相同的方式来进行推导,故后人将此方法叫做m推演型滤波器 。
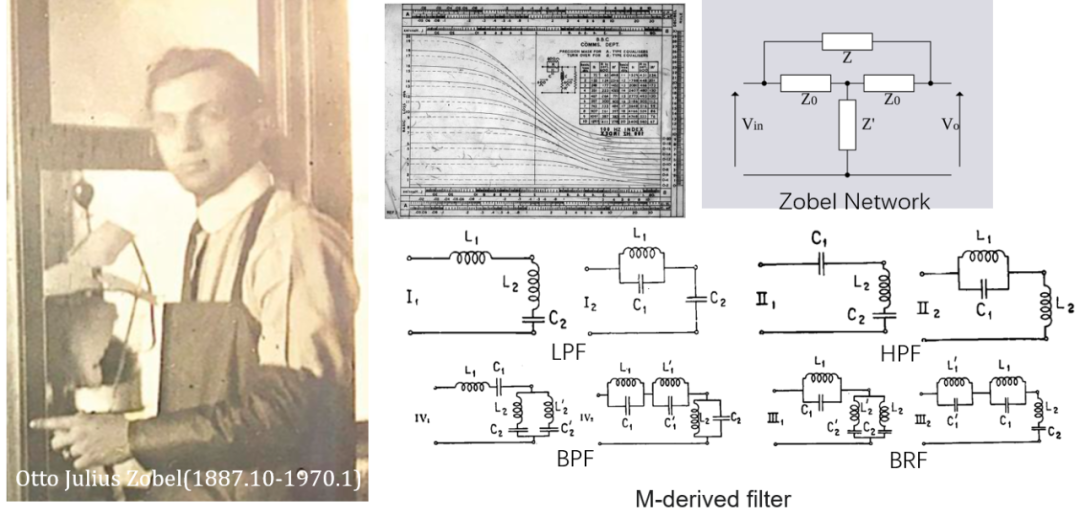
前面滤波器分析和设计都是基于传输线来设计,即假设滤波器阶数为无穷,然后分析一个滤波器节(L节或PI节或T节)的性质来进行设计,其中的诀窍就是保证每个节前后阻抗匹配(镜像阻抗匹配),这样m推演型滤波器(截止特性不好,过渡带好)就可以和定k滤波器(截止特性好,过渡带不好)随意组合而不会出现失配,从而丰富了滤波器的设计 。
但是镜像法设计滤波器缺陷也是非常明显:
- 滤波器的推导都是在匹配状态下进行的,实际情况可能更加复杂,源和负载阻抗可能不匹配,这种情况下镜像法设计将会失效;
- 由于推导过程也假设了阻抗在整个频段内是不变的,即阻抗不会随频率变化而变化,但是实际上阻抗会随着频率变化而变化,尤其是接近过渡带的地方,反射严重,频响的peaking会比较大;
- 通带内的纹波也没有得到很好的描述,只有一个传播常数(propagation constant)来描述插损,在镜像法设计中始终假设滤波器通带是平坦的,实际设计中非常关心通带纹波的情况;
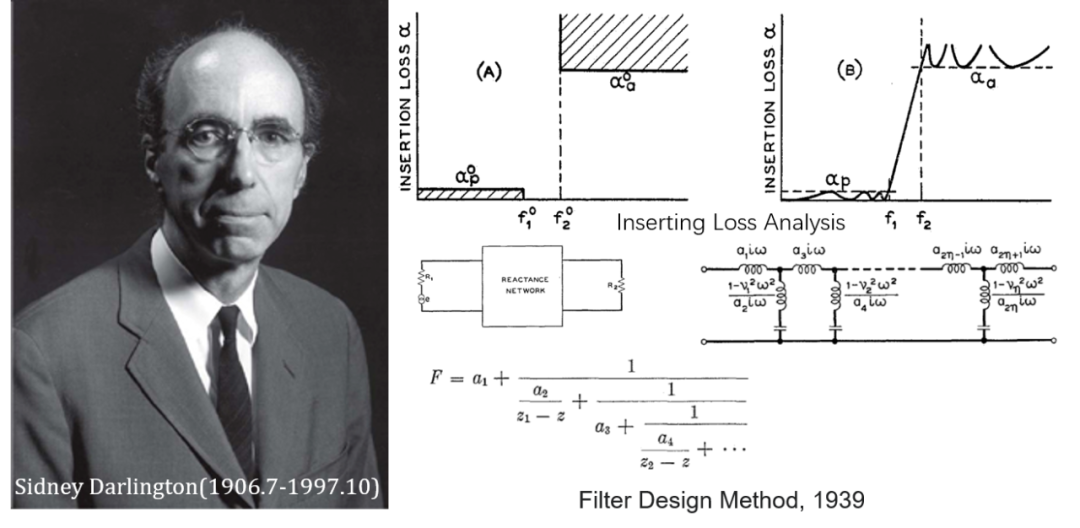
达林顿(Sidney Darlington, 1906.7-1997.10),没错就是那个发明达林顿管的达林顿发展了电路网络理论,并且对滤波器分析理论进一步发展。1939年提出了镜像参数分析法的概念,并提出了使用插入损耗法来分析滤波器电路的新方法 ,这一分析方法开启了崭新的现代网络综合理论。
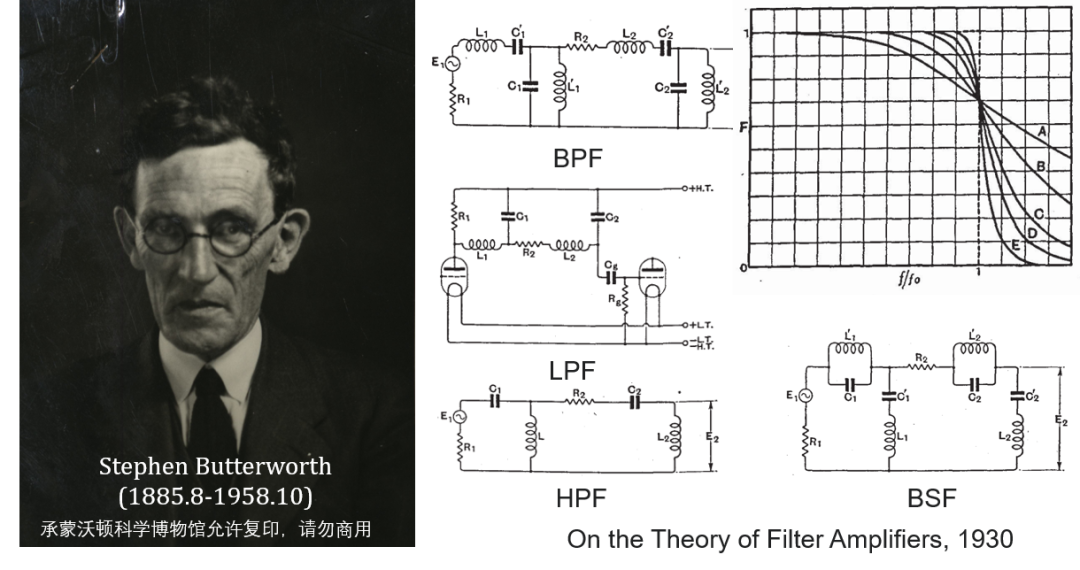
巴特沃斯(Stephen Butterworth, 1885.8-1958.10)是英国物理学家,发明了巴特沃斯滤波器,相关文章1930年发表于《无线电工程》杂志上 。他定义了一个多项式 ,工作的目的是使用电路去逼近这个多项式,巴特沃斯仅仅给出了2阶和4阶的计算,高阶实现方式是使用多级,中间插入放大器来隔离前后级,从而可以很巧妙的避免使用复杂的计算,设计出符合最平坦响应滤波器,最后他还给出了各种不同类型的滤波器设计表格,巴特沃斯的工作可谓是开创性的,同时也是第一个设计有源滤波器的人。
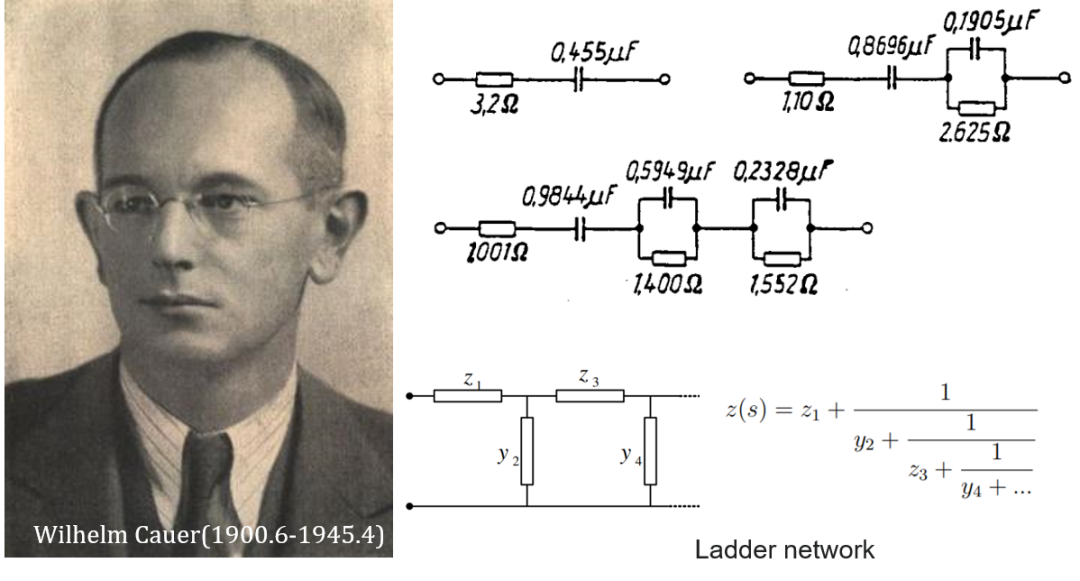
卡尔(Wilhelm Cauer, 1900.6-1945.4)是德国数学家和科学家,滤波器界扛把子的存在,之前的滤波器设计工作如果说是惯性制导,卡尔的工作可以说是做到了滤波器精确打击的效果,他用其扎实的数学功底解决了滤波器综合中的种种难题。卡尔在1926年的博士论文中就提出了网络综合的相关问题,做了很多铺垫性的工作,其中他提出了网络综合的三个主要任务:
- 传递函数的可实现性(realizability)
- 找到实现所需响应的近似(approximation)
- 网络函数的实现与等价(realization and equivalence)
这些工作都是围绕着单端口阻抗进行,这是由于卡尔找到了由阻抗函数直接导出电路的方法,也就是我们现在一直在使用的连分式展开法将阻抗表达式和梯形网络元器件值联系在一起。他摈弃了之前镜像设计,系统性的解决了滤波器的设计,他首先提出使用切比雪夫来进行近似(1930-1931),后来又使用椭圆函数来进行近似(1933),这样既可以控制通带纹波又可以控制阻带纹波,现在我们通常所说的切比雪夫滤波器和椭圆滤波器实际上都是卡尔发明的,有的地方将椭圆滤波器也叫卡尔滤波器。由于历史原因卡尔的命运却是悲惨的,他在二战柏林沦陷期间被苏联士兵所杀害,年仅45岁。
本文主要研究无源滤波器,其他关于有源滤波器的部分见参考文献 .
滤波器设计发展时间线
滤波器设计发展时间线和重大历史事件对比:

阶梯网络综合方法
阶梯网络综合的方法是由传递函数H(w)得到和功率的关系,功率和反射有关系,反射和输入阻抗有关系,输入阻抗和阶梯结构有关系,最后得到H(w)和阶梯结构的关系 。
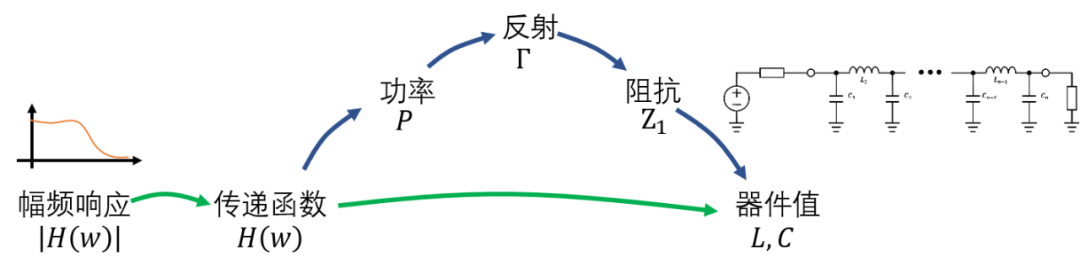
以上是对阶梯网络的总结,后续会对其中的原理进行推导分析。
PS: 封面图给出了复平面巴特沃斯滤波器极点分布情况:
-
有源滤波器与无源滤波器的区别2025-06-18 1400
-
什么是无源滤波器2024-10-16 4149
-
无源滤波器和有源滤波器的区别2024-09-26 2590
-
如何设计无源lc滤波器的频率2023-12-01 2739
-
有源滤波器和无源滤波器的区别?2023-08-11 6558
-
无源滤波器由什么组成及作用是什么2023-02-24 3422
-
有源滤波器和无源滤波器的区别2021-07-22 3702
-
无源滤波器的类型2018-08-30 18906
-
无源滤波器的原理,和无源滤波器电路设计详细解析2017-05-03 21218
-
转:有源滤波器和无源滤波器2011-07-28 6929
-
无源滤波器基本概念2010-04-13 7092
-
无源带通滤波器电路,有源带通滤波器原理图2010-02-26 9384
-
模拟滤波器实验2009-05-10 5486
-
无源与有源滤波器频率特性研究2008-09-24 13543
全部0条评论

快来发表一下你的评论吧 !

