怎么设计模拟无源滤波器-2

本节主要介绍LC梯形网络的综合方法，包括经典镜像法、插入损耗法和转移函数法这三种网络综合的设计方法。

现代滤波器网络综合所解决的问题

现代滤波器综合技术所解决的问题非常有限，下图是对模拟无源网络做一个简单分类总结:

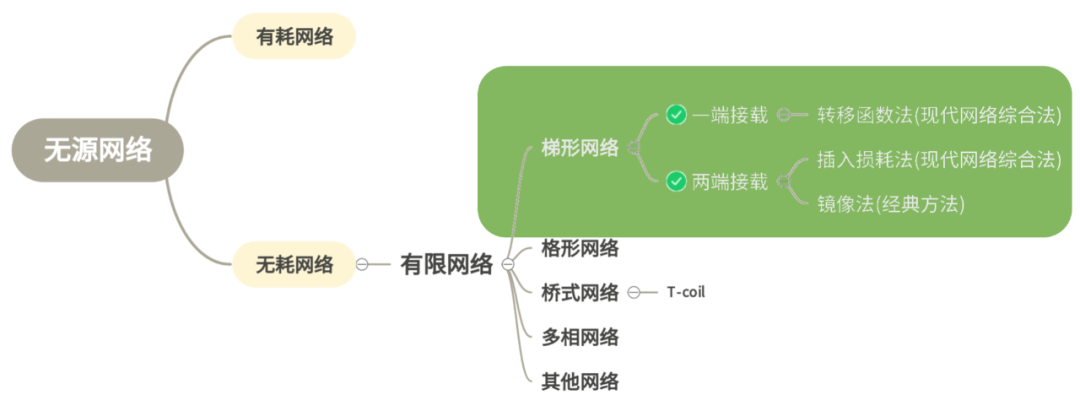
图中绿色阴影部分是本节内容所能够解决的部分，其他网络目前笔者并未见到比较成熟统一的理论，后续有机会我们再进行深入分析和研究。

滤波器综合技术是数学和电路两门学科的交叉学科，要掌握这门技术，需要同时掌握这两个领域的知识。电路中涉及到电路分析、微波射频、信号系统等等理论，而在数学就涉及到更多，诸如矩阵论、复变函数、特殊函数、函数逼近等等知识。

可以预见的是随着计算机技术，AI技术(滤波器综合的本质上是依照特定功能设计出符合一定结构的网络，所以当下AI等技术的发展可以说给滤波器综合技术带来了新的希望)的发展，所有关于滤波器网络综合的问题在可预见的未来一定会得到很好的解决。

滤波器综合的基本知识

前提

本节模拟无源滤波器综合必须：

1. 滤波器网络结构为梯形
2. 滤波器网络除输入和输出外，剩下的全部是电容和电感，即滤波器网络为无耗网络，阻抗的零极点必在虚轴上交替排列, 滤波器是无条件稳定的,对于输入的任何激励不会出现自激,网络函数中极点不在右半平面
3. 滤波器为有限阶

由连分式综合出梯形网络

LC梯形网络综合离不开网络的连分式展开(continued fraction)这个工具，它是荷兰数学家“连分式分析之父”的斯蒂尔吉斯(Thomas Joannes Stieltjes)所提出，连分式可以用有理数来表示无理数，对于无理数 我们有如下连分式表示方法： 在电路设计领域，梯形网络(Ladder network)的阻抗可以用连分式来表达，如下:

所以可以得到此梯形网络的连分式表示： 这种连分式写法可以很方便的依据表达式综合(Synthesis)出电路来，如上述的 用电阻来实现就为：

连分式可谓将网络的输入阻抗和梯形网络紧密的联系起来了，那么一个梯形网络的输入阻抗和其传递函数之间又有什么关系呢？

网络函数

下面我们通过简单的2阶LC低通滤波器来进行分析，让大家对滤波器电路分析有一个直观的认识：

从上图可以看到即使分析一个简单的滤波器，最终传递函数公式也是比较复杂且没有什么规律可循。倘若再分析3阶或5阶滤波器就更费劲了。那么我们应该如何去分析呢，若我们将滤波器看成一个黑盒子来研究，这将大大降低电路分析难度。

滤波器电路黑盒子有4个端口，分别为1,1',2,2'，前面我们知道，输入阻抗 可以用来描述一个梯形网络的结构，所以在4端口网络中，我们尽量往Z1上靠，所以在这里我们选择阻抗Z网络。 式中 表示4端口网络的输出口开路时的输入阻抗，注意到滤波器综合的前提条件2，可以得到所有Z参数的零极点都在虚轴上，非常容易研究其性质。

滤波器网络输入和输出可以交换的(互易),所以有 。

有了四端口阻抗网络定义，我们可以找到平时非常关心的网络转移特性，即输出和输入的关系，转移阻抗 就是比较常见的一个转移函数，它和Z网络的关系如下(对 进行归一化处理): 若给定网络的转移阻抗 ，我们可以通过表达式结构求出 和 ，再由 的零极点，将 的极点一步步去除，从而可以综合出对应的滤波器。

对于Z网络还有一个重要的性质是 包含网络的所有极点，这个可以由电路方程的解中都包含整个参数矩阵的行列式来理解，这一点在电路综合中非常重要。

阶梯网络综合方法

两端接载-插入损耗法

两端接载的梯形网络综合采用插入损耗法，使用插入损耗法来综合网络的方法是由达林顿(Darlington)在1939年提出的，这种综合法流程在前文中有提到过，基本综合流程如下图所示，若需要了解更多可参考插入损耗法原理推导 ：

下图显示一个3阶巴特沃斯低通滤波器的综合过程：

注意此滤波器综合的频率为 ，另外图中 的定义与初始达林顿的有所区别，以便和现代传递函数对应。

上述方法是由传输功率-->反射-->输入阻抗这一基本线路进行网络综合.上述综合成立的条件是网络两端都需要端接，若任意一端开路或短路， 的定义将会失效，故需要使用插入电压比来进行定义和计算。

一端接载-转移函数法

前述插入损耗法仅仅适用于两端接载，当滤波器网络一端短路或开路，我们必须改变传递函数的定义，由插入损耗法可知 , 所以理所当然的使用电压转移函数 进行定义：

这样定义后由于源端全反射，不能用反射理论来进行分析，只能回归本源使用前述的4端口网络相关理论来进行分析，用 和 得到: 若将 和 对 进行归一化，即可得到和转移函数 一样的表达式，这样可以通过极点移除法来综合了。

下图显示一个一端接阻的3阶巴特沃斯低通滤波器的综合过程：

图中由一种传输函数可以得到4种不同的滤波器端接结构，从中可以得到规律，从端接电阻看过去的阻抗或导纳不变。

上述由传递函数推导出Z或Y参数的一个技巧是将传递函数的分母分为偶部M和奇部的和，这样是为了凑出 、 、 、 ，这是因为梯形网络的策动点阻抗或导纳为方次差1的两个多项式之比（由网络的稳定性推导而来）。

从之前的网络综合可以看出，当传递函数一定，综合出来的网络可能有很多种。

镜像法综合

由于镜像法综合历史非常悠久，最初滤波器被发明以来就使用了这一分析方法，我们需要清楚这一分析观点--波的分析方法。很多最初的想法在现在微波领域任然在使用，镜像法在行波放大器设计中也能用到 。这里只对镜像法做一个概念入门，并给出一个简单的设计实例。

定k滤波器

之前已经介绍过镜像法最早是由传输线线理论发展而来，其结构是无限长周期结构，为了简化分析我们将无限长周期结构拆分为一个T节或PI节，如下所示：

这种简化的关键是T或PI节输入和输出阻抗都相等，并且在频率为0处的阻抗都和传输线的特征阻抗相等,即 ，这也是定k的来源。另外由阻抗公式可以看到当根号下为0时即可得到传输线的截止频率 。

所以可以通过以上两式求得滤波器的参数值： 定k滤波器是最简单的滤波器，由于输入输出阻抗匹配，所以若需要增加滤波器阶数可以简单的将T型或PI型节级联即可，这一点在射频滤波器设计中非常常见。

定k滤波器的缺点也很明显:

• 滤波器截止特性并不好
• 滤波器截止频率点并不非常准确
• 可以看到滤波器输入输出阻抗匹配特性并不是太好，若输入或输出接纯电阻作为源或负载，只有一个点能够匹配上。

为了克服上述缺点，佐贝尔(Zobel)发明了m推演型滤波器(m-derived filter)。

m推演型滤波器

m推演型滤波器设计基本思想和定k滤波器一样，保证滤波器节网络的输入输出阻抗相等(便于滤波器级联)，并且找出阻抗基本恒定的网络(便于和源和负载匹配)。其推导原理如下图所示：

由定k滤波器T型节出发，将电感乘以一个参数m，这样我们得到另外一个T型网络，并令对地臂阻抗为 ，这样我们令这个新的T型网络和定k滤波器T型节阻抗相同，从而推导出 为一个电感和一个电容串联而成，对地臂提供了一个传输零点，从而使得传递函数出现零点，从而可以在截止频率处提供更为陡峭的衰减。

由m推演型的推导过程可知，m推演的T型结构和定K的阻抗相等(和m无关)，阻抗会随着频率频率变化而剧烈变化，见图中 表达式；但是m推演型的PI型结构阻抗却随m的变化而变化，在m=0.6时，阻抗会呈现比较恒定的值（图中右上图所示），这就有利于和源和负载进行匹配，所以一般设计中m=0.6的m推演型半PI节会作为输入和输出匹配节来使用。

中间节点就使用正常的T型节和定k滤波器节。

当m=0时，m推演型滤波器就化为定K滤波器，即定k滤波器是m推演型滤波器的一种特殊情况。

由于m推演型滤波器的T型节阻抗和m值无关，所以在滤波器综合过程中可以任意改变T型节位置和增加滤波器阶数，整个滤波器匹配特性将保持不变。改变m的值可以移动传输零点位置，所以可以有选择性的抑制我们所需要抑制的频点。

下图给出了综合一个截止频率为 ，希望在0.17Hz以及无穷大处有最大抑制点，阻抗匹配到1Ω。

由阻抗和截止频率可以计算出基本的L和C值，同定k滤波器设计： 传输零点位置和m的关系如下: 得到0.17Hz处传输零点 ，进而得到m推演型T型节的0.17Hz的传输零点。

详细综合过程如下：

小结

上述3种网络综合方法各有优缺点，并不存在一个万能的综合方法，后期小程序软件设计中也会依据不同的端接类型来选择不同的综合工具实现。接下来工作是进行网络仿真方面的工作，若感兴趣的同学可以后台留言交流。