

什么是通用梯形电路网络分析和仿真
模拟技术
描述
本节主要对计算机电路分析理论进行概要讲解,并结合实际滤波器电路分析,最后使用Matlab实现了一个通用梯形滤波器Mini仿真引擎(GitHub免费下载)。
电路分析基础
从电磁现象被人们发现以来,人们不断探索先后发现了库伦定律(Coulomb's law, 1785年,通过实验得出静电力遵循平方反比规律)、毕奥-萨伐尔定律(Biot-Savart Law, 1820年,表明电生磁)、安培环路定律(Ampère's circuital law, 1826年,表明电生磁,并且磁)、法拉第电磁感应定律(Faraday's law of electromagnetic induction, 1831~1845年,表明磁生电),依据这些定律,麦克斯韦(Maxwell's equations)于1864年提出了著名的麦克斯韦方程组,于是统一了电和磁。
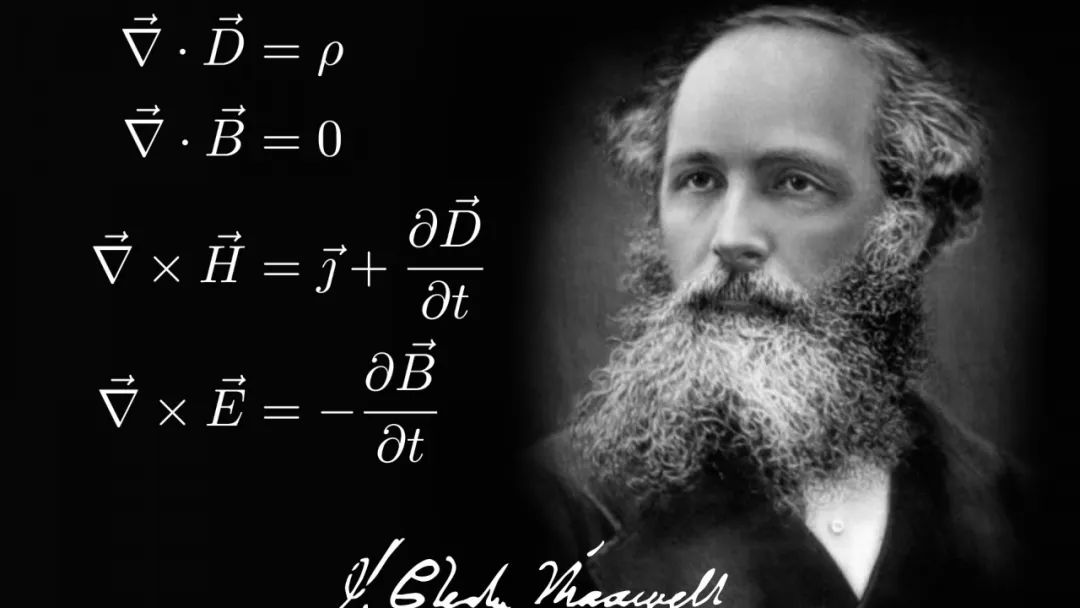
都说麦克斯韦统一了电和磁,那么我们从麦克斯韦方程组出发是否能够推导得到电路分析的相关理论来吗?这一节我们就麦克斯韦方程组的理论框架下来理解电路分析相关理论。
在电路分析领域,有三大法宝: 欧姆定律 ,KCL和 KVL 。
查阅相关文献资料发现比较遗憾的是麦克斯韦方程组并不能导出如欧姆定律(Ohm's law) ,欧姆定律是独立于麦克斯韦方程组的,也就是所谓媒质的本构关系(Constitutive equation) 。欧姆定律是欧姆基于一系列的实验所获得的结果,并在1827年发表在《直流电路的数学研究》(The galvanic Circuit investigated mathematically)一文中。
那么欧姆定律如何来推导呢?现在比较广泛的推导是使用德鲁德模型(Drude model),也即使用微观自由电子气模型来推导 。
基尔霍夫定律(Kirchhoff Circuit Laws, 1845年)是可以使用麦克斯韦方程组来推导的,基尔霍夫第一定律也即基尔霍夫电流定律(KCL)可以由电场散度为0求得;基尔霍夫第二定律也即基尔霍夫电压定律(KVL)可以由静电场旋度为0求得。电路理论是电磁场理论在一定条件下的近似结果,器件必须在准静态范围内工作,即工作波长远大于电路尺寸 。
有了欧姆定律和基尔霍夫定律我们就可以进行电路分析和计算。
梯形电路网络方程
下面以无源梯形网络设计举例来实现电路分析步骤。由于这种网络结构属于平面结构,而且结构相对简单,所以不必使用关联矩阵(Incidence Matrix),可以直接使用网孔法(Mesh Analysis)列方程来进行电路分析。
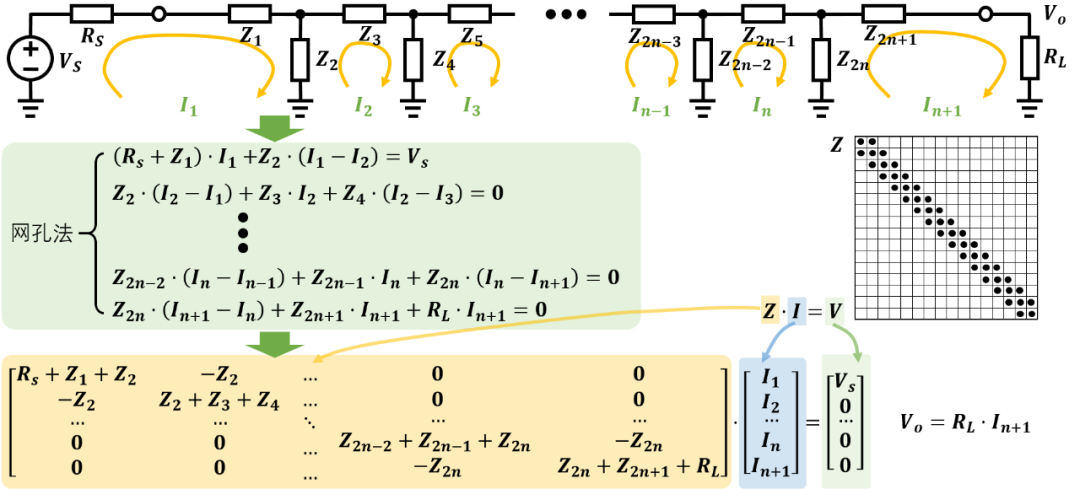
上图电路结构可以用来分析所有梯形滤波器,滤波器阶数为 。若需要构造 型结构滤波器,则可以令 ;若需要构造偶数阶滤波器,则可以令 ,这时滤波器阶数为 。
为了适应不同的滤波器类型和适应实际器件模型(参考电容等效和电感等效),特定义阻抗节类型(Type)如下:
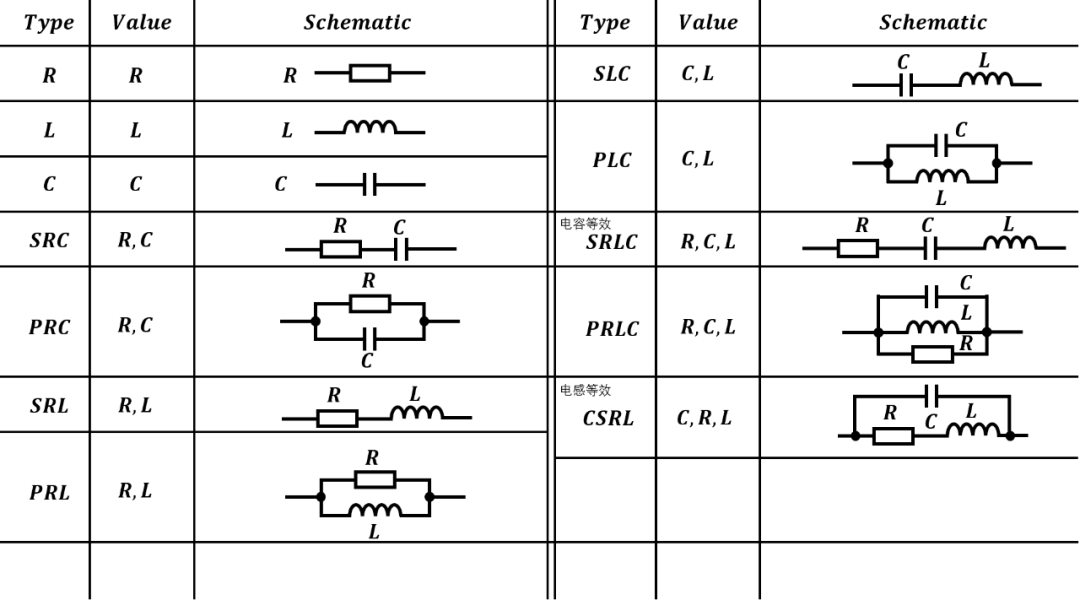
有了上述电路矩阵方程,我们可以依据s参数求解出AC特性,只需要求解方程:
接下来就是各路仿真软件的核心--线性方程组的稀疏矩阵(Sparse Matrix)求解。
稀疏矩阵求解
由上节得到的电路Z矩阵大部分元素为0,属于稀疏矩阵,常用的直接计算机解法是矩阵的高斯消元(Gauss elimination)、UL分解(LU factorization)、科列斯基分解(Cholesky decomposition) 或其改进的LDLT算法,UL分解在早期电路分析中使用特别多,优化算法在如何减小存储量和计算量这个方向上努力(算法会破坏矩阵的稀疏性,或者改变矩阵结构),尤其是UL算法可以在不怎么增加额外的存储空间情况下直接在源矩阵上计算,无需额外存储开销,这样可以求解大型电路方程 。
对稀疏矩阵进行数值求解的另外一条路也非常不错,即稀疏矩阵迭代计算,这种方法的好处是利用了前一次计算结果,可以通过有限步计算快速将求解误差收敛到指定范围内,并且此算法并不会破坏矩阵的稀疏性,迭代计算在非线性电路分析、电路优化、灵敏度分析、参数扫描中非常适用。迭代计算方法有雅克比(Jacobi)迭代求解、高斯-赛德尔(GS, Gauss-Seidel)迭代求解、超松弛(SOR, Successive Over-Relax)迭代求解、共轭梯度(CG, Conjugate Gradient, 1951)迭代求解 ,这几种方法层层递进,Jacobi方法最原始,GS只是每步都利用前一次计算的值,SOR提供了一个可选的因子可以调整迭代步长,CG提供了每次迭代的最佳步长。
本想着此次主要针对小程序电路分析不需要这么大费周章的将矩阵求解这部分深入太多,但是考虑到后续电路优化,有必要将CG迭代算法做深入研究。CG迭代算法将一次函数运算转化为构造的二次函数的极小值的运算,二次函数极值计算就可以使用梯度下降法来求解了,CG迭代算法可以说是进阶版本的梯度下降算法,他不是用最小梯度方向搜索到终点,而是用共轭梯度方向搜索到终点。CG迭代算法文末有参考学习文章,写得通俗易懂,有兴趣的同学可以移步到参考文献 。
CG迭代算法步骤如下:
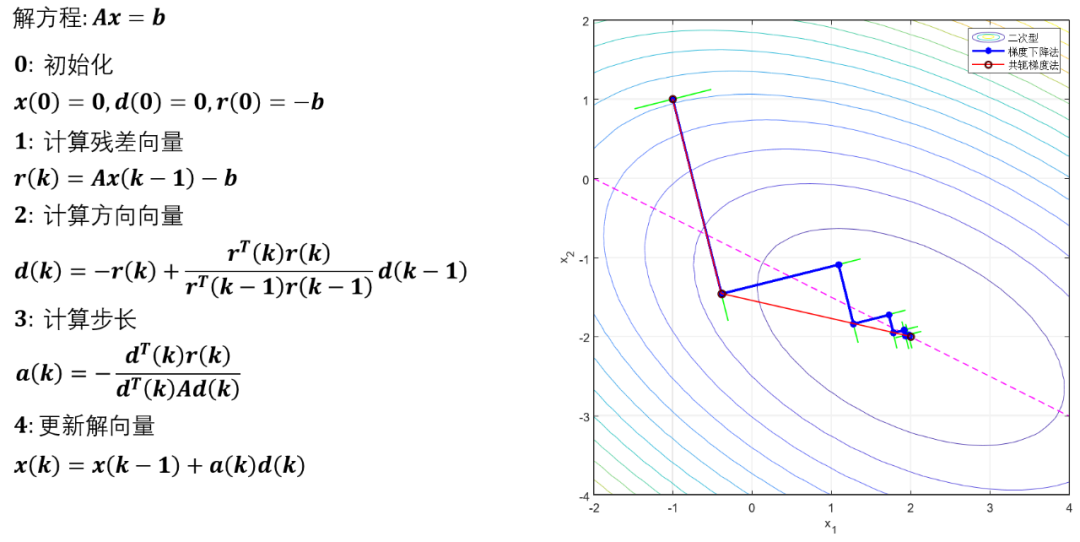
上图之字形蓝色曲线是梯度下降法迭代过程,红色线是共轭梯度法迭代过程,从中可以看到CG迭代收敛速度远远优于梯度下降法的。有人可能会问,为什么不直接从初始点直接一步到最终点呢,对,之前的高斯消元法等等就是这里的一步迭代法。
从计算复杂度上来讲,CG迭代算法的计算复杂度是 ,高斯消元法约为 ,所以从计算复杂度上来说CG迭代算法并没有优势。CG迭代法每迭代一次可以将整个矩阵计算一次,能够从全局计算出出一个近似的结果,对于很多实际问题,我们只要控制好精度,就只需要较少的迭代次数就可以达到工程要求,最终可以使得迭代法实际计算复杂度远远小于直接法。高斯消元法在稀疏矩阵的应用中会遇到0元素的填充问题,这会给编程带来非常大的不便,而且影响矩阵的稀疏性。
对于滤波器软件设计,其中很重要的频率响应,频率响应的计算需要使用到频率扫描,若扫描点比较密集,假设是N,那么我们使用高斯消元法对每个频率点进行计算是独立的,这样计算量就非常大。但是若使用CG迭代计算,那么我们可以利用前一点计算的结果,可以大大减小后续点的迭代次数,计算量会响应减小。
实际仿真中发现若使用CG迭代来进行滤波器仿真计算,那么你将得到的是错误的结果,梯形网络矩阵计算并不收敛!这是由于CG只针对对称正定矩阵(symmetric and positive-definite)才有效,而电路方程是复数方程,其Z矩阵为一个非厄米特矩阵(Non-Hermitian矩阵),需要使用双共轭梯度法(BiCG, Biconjugate Gradient,1976) 来对其进行求解,BiCG迭代算法可以支持计算非对称正定矩阵,由于BiCG算法并不稳定 ,所以后人又提出了CGS(Conjugate Gradient Squared, 1989) , BiCG-Stab(Biconjugate Gradient Stabilized, 1992) 算法,这样才真正将CG算法走上了实用。
另外,对矩阵的预处理(Precondition)也非常重要,因为所有之前的算法都会存在一个矩阵不能让结果收敛到给定精度。对线性系统迭代计算算法汇总文档请参考 。
直接法(UL分解)计算和BiCG迭代计算对比的Matlab代码都上传至GitHub上 [https://github.com/etools361/SolveSystemOfLinearEquations.git]。
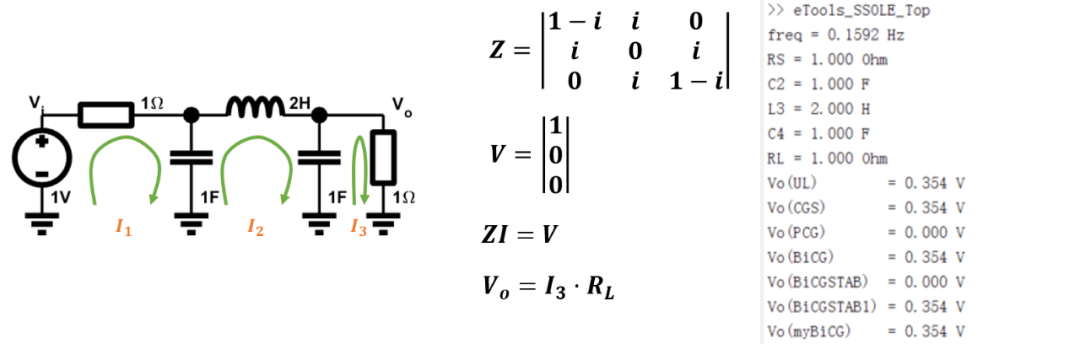
梯形电路网络仿真引擎
由电路方程节的方法,按顺序定义器件类型和值,比如3阶Butterworth滤波器网表定义如下(上图是PI结构,下图是T结构):
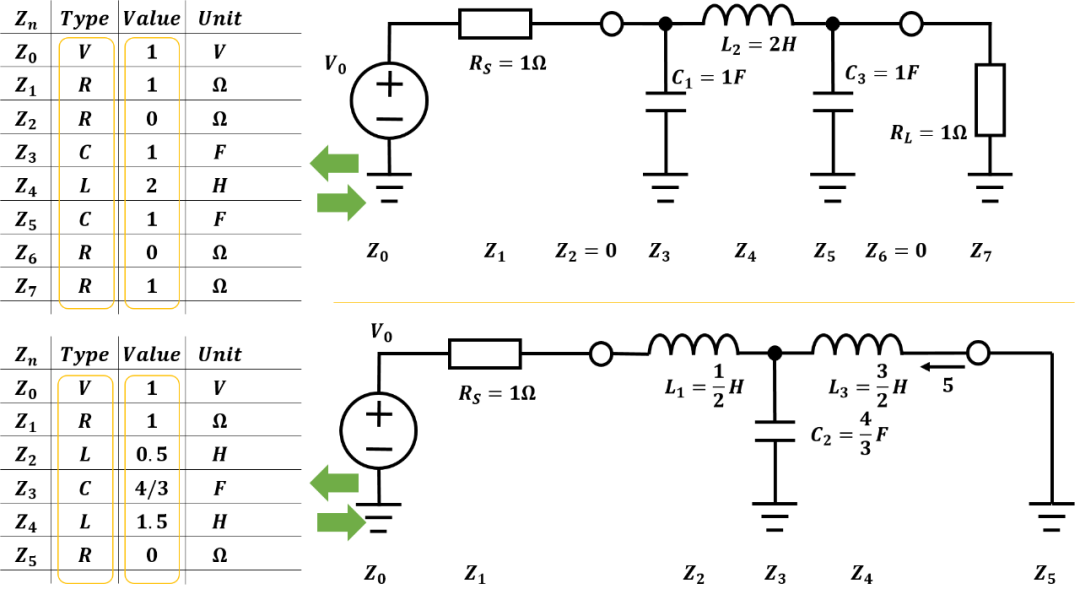
从上图可以看出,我们只需要在内存中存储Type和Value这两列数据即可还原梯形结构。
由上述网表结构可以构造出Z矩阵,然后使用线性方程组计算即可得到仿真值。
程序输入是电路网表、AC参数设置,输出为幅频传输特性曲线。
使用matlab实现一个 通用梯形网络仿真引擎 (代码已经上传GitHub,有兴趣的童鞋可以去下载 [https://github.com/etools361/LadderNetworkSimEngine.git]),实际运行结果如下:
- 两端接载情况, 3阶巴特沃斯低通滤波器
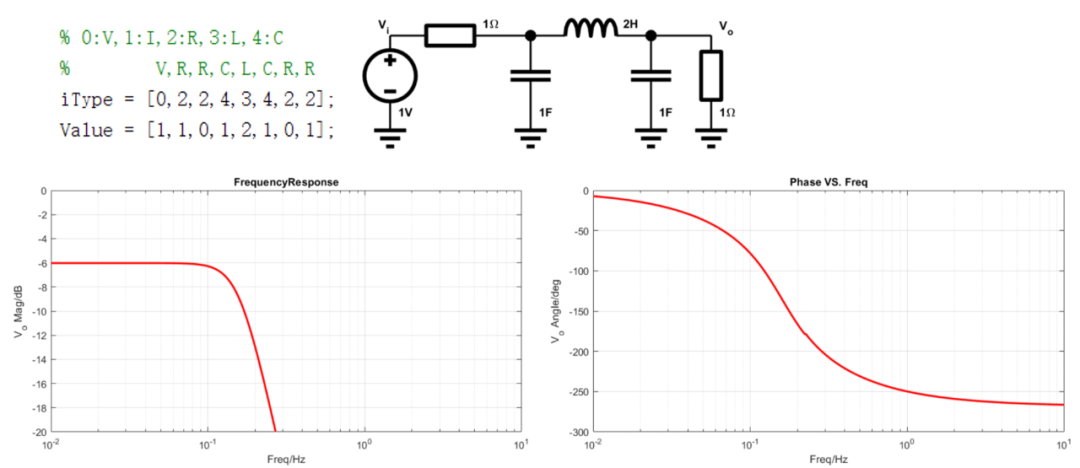
- 一端接载情况, 3阶巴特沃斯低通滤波器:
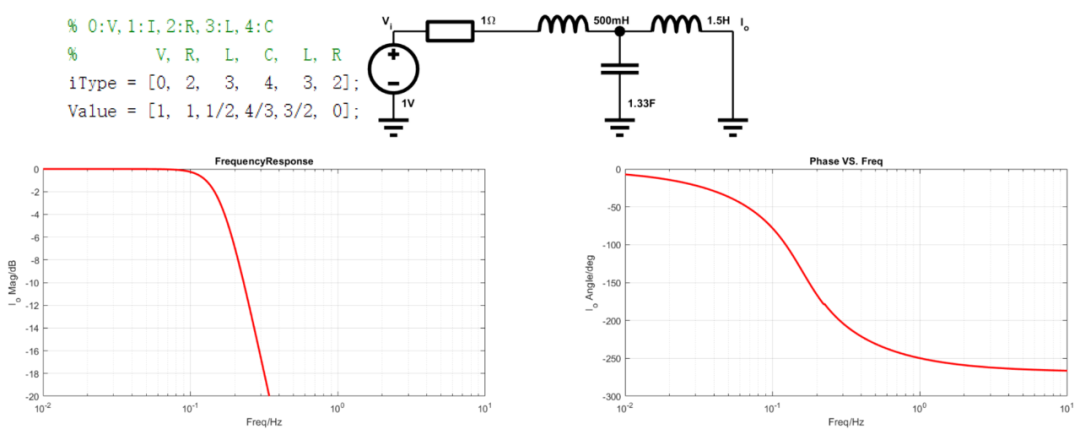
- 7阶切比雪夫高通滤波器:
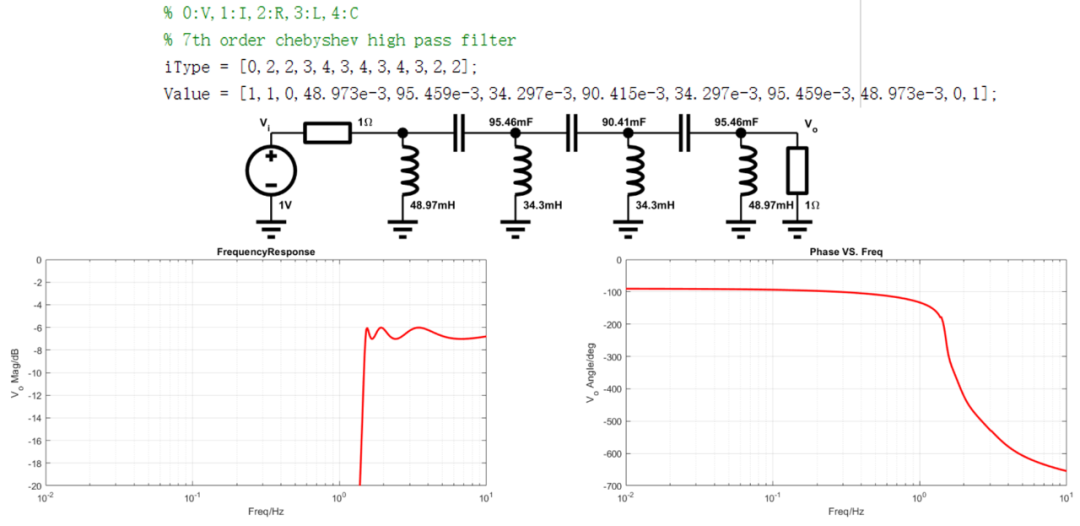
-
矢量网络分析仪与标量网络分析仪技术差异与应用场景解析2025-12-11 1196
-
矢量网络分析仪的使用说明2024-05-13 5460
-
网络分析仪的分类2024-05-08 1718
-
使用Matlab实现了一个通用无源网络仿真引擎2023-02-20 1815
-
网络分析的基本原理,怎么使用网络分析仪?2021-04-12 2648
-
网络分析与网络分析仪的详解2018-05-02 25880
-
怎么用Orcad Pspice 测电路网络参数值??2015-03-31 2141
-
电路网络潮流的调整控制2013-04-10 2063
-
网络分析仪基础2012-01-17 1730
-
网络分析器,网络分析器原理是什么?2010-03-22 1257
-
模拟电路网络课件 第十节:图解分析法2009-09-17 3293
全部0条评论

快来发表一下你的评论吧 !

