

Butterworth滤波器设计的详解
模拟技术
描述
从本节开始深入讨论各种不同滤波器设计,本节是Butterworth滤波器综合设计,结合之前电路仿真的工作,现将Butterworth型滤波器集成到了滤波器设计App中,并提供一个试用版本,提供GitHub开源链接。
Butterworth滤波器特点和用途
Butterworth滤波器是Stephen Butterworth于1930年首先发表于众参考[模拟无源滤波器设计(一)],特点是其具有最平坦频率响应,故很多地方将其称为最平响应滤波器 ,其最平坦响应滤波器可能会被有些工程师所误解,认为其频率响应最为平坦,实际上这里最平响应是指在DC附近(低通滤波器)具有最平坦响应,也就是说在频率为0处其频率响应高阶导数为0(注,由于其传输函数中含有特征多项式 , 为滤波器阶数,所以不管求导多少次都在0频率处取得0值)。实际上Butterworth滤波器在接近截止频率处频率响应并不好。
Butterworth滤波器的另外一个特点是其数学分析和网络结构都比较简单,有较好的相位特性,滤波器所需要的器件容易获得故其得到了广泛的应用。
关于Butterworth本人的相关信息可以参考翻译文章。
匹配型Butterworth滤波器综合
匹配型Butterworth滤波器的幅频响应为: 是 对 归一化频率,即 .
由之前讨论的由功率反射一套理论可以由幅频响应得到功率损失,进而由反射相关理论得到输入阻抗,最后由辗转相除法得到器件值,由之前的阻抗值:
其中 固定为 , 比较难些,称其为巴特沃斯多项式,这里直接引用计算得到的通项公式: 式中: 由辗转相除的方法计算前几项并总结规律得到,第 个枝节器件值为:
任意频率处衰减的滤波器综合
以上是对截止频率为-3dB下的滤波器综合,当截止频率为 并且此处的频率响应为: 在 的衰减为: 系数 和反射系数有关: 当反射系数 为0.707时,有一半功率反射时,即-3dB衰减,有 ,这时频率响应曲线和匹配型公式一致。
此时对应的元件公式为: 其中:
由衰减确定滤波器阶数
设滤波器综合的通带频率为 ,其衰减为 dB,截止频率为 ,其衰减为 dB.示意图如下:
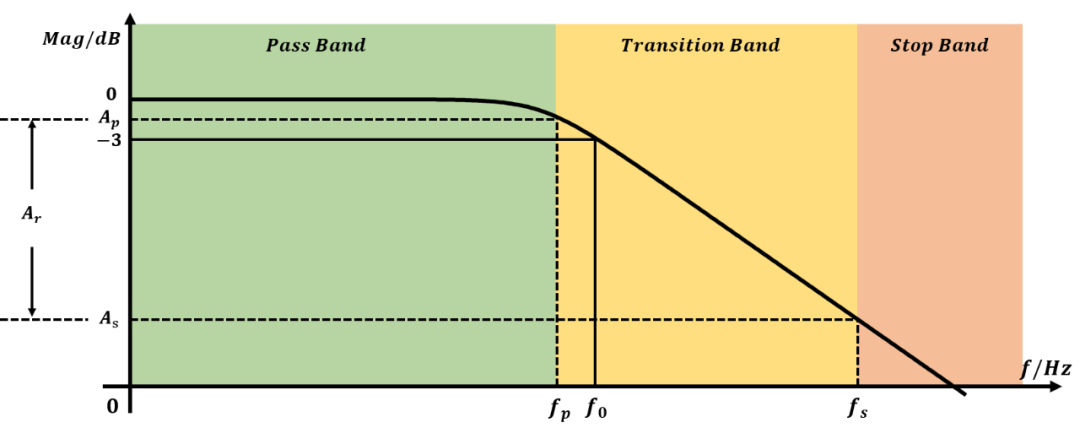
所要求的通带到阻带的衰减是 ,可以通过计算得到衰减和阶数关系为:
非匹配型Butterworth滤波器综合
上述公式是匹配型滤波器设计公式,当输入 输出 阻抗不匹配时,其传输函数: 其中,由最初的定义,当 时和匹配型滤波器一样:
令: 这里实际上只需要讨论一种情况即可,如 ,则对于 的情况只需要简单的将电路器件反序过来即可。
系数 和衰减 的关系为: 具体归一化的LPF滤波器器件值为:
详细推导过程可以参阅 。
设计实例
这里以3阶Butterworth低通滤波器为例说明,设 ,得到:
所以得到: 由于这里的参数均是相对于T型网络 计算的,所以最终的电路参数为: 电路如下:

不同滤波器通带类型之间的转换
只要有了低通(LP)滤波器原型,那么高通(HP)、带通(BP)、带阻(BR)滤波器参数可以非常容易的求得。
- 低通滤波器到高通滤波器
我们只需要将 ,都知道电容的容抗为 ,电感的感抗为 ,所以将其中的 替换为 得到:

这样即可将低通转换为高通,由于 和 之间是倒数的关系,当 时那么 ,当 时那么 ,当 时那么 ,这也就是说低通的阻带是高通的通带,低通的通带是高通的阻带,低通的截止频率和高通的截止频率相等。
- 低通滤波器到带通滤波器
我们只需要将 ,这里可以将带通滤波器理解为高通滤波器+低通滤波器组成(两个滤波器串联),从转换公式可以看到 代表低通, 代表高通,两者叠加变为带通,我们用上面的办法分别对低通的电感和电容做 替换:

这样即可将低通转换为带通,由于 函数是一个对钩函数,即两头高,中间低,当 时那么 ,当 时那么 ,当 时那么 ,这里是以实频率来说的,实际上电容电感阻抗是有虚部的,为简单直观起见这里并未考虑。
- 低通滤波器到带阻滤波器
带阻可以理解为带通的倒数,我们只需要将 ,这里可以将带通滤波器理解为高通滤波器//低通滤波器组成(两个滤波器并联),从转换公式可以看到 代表低通, 代表高通,两者叠加变为带阻,我们用前面的办法分别对低通的电感和电容做 替换:

这样即可将低通转换为带阻,分析方法和前面类似,读者可以自行分析。
滤波器的零极点分析
Butterworth低通滤波器的极点在一个圆上,可以通过 的公式(这里仅仅讨论匹配型Butterworth)可以推导: 令公式的分母等于0,得到极点位置公式为: 根据欧拉公式 并且做个拓展 后可以得到: 可见 上的点落在一个圆上,我们取复平面的左边极点即可得到 的通项公式。
另外滤波器频率响应曲线和零极点息息相关,所以在滤波器电路分析中我们可以通过零极点来判断滤波器状态。典型的应用是滤波器电路参数和零极点的灵敏度的关系,从而可以找出敏感器件。
不同通带类型滤波器零极点图如下:


高通和低通的极点相同,零点位置不同而已;带通和带阻的极点相同,零点位置不同。
PS:上述零极点分析可以在文末的GitHub仓库中滤波器设计软件自动生成。
Butterworth滤波器设计软件
基于Matlab的appdesign工具开发了一套Butterworth滤波器设计软件,主要特点是:
- 支持4种不同滤波器通带类型(LPF,HPF,BPF,BRF)设计
- T型和PI型结构滤波器随意切换
- 可以设置阻带衰减决定滤波器阶数
- 可以设置通带衰减来综合滤波器
- 可以随意配置负载和终端阻抗,并支持一端接载(源端电阻短路,源端电流源,终端开路,终端短路)设计
- 可以幅频响应分析、零极点分析、瞬态分析
LPF设计举例
设计一款-3dB截止频率为1GHz,7阶低通Butterworth滤波器,输入输出阻抗为50欧姆,设计过程如下:

最终设计参数如下:

PZ分析结果如下:

BPF设计举例
设计7阶带通Butterworth滤波器,输入阻抗为50欧姆,输出开路,并进行瞬态仿真,设计过程如下:

最终设计参数如下:

瞬态仿真结果:

上述设计的带通滤波器只有一种综合结果,其中Tee和PI选择并没有任何作用。
程序的Matalb源码已经上传GitHub中 (https://github.com/etools361/MatlabFilterDesignApp),有兴趣的同学可以下载试用体验,当然也欢迎技术交流。
- 相关推荐
- 热点推荐
- 滤波器
- 频率响应
- Butterworth
-
滤波器问题?2012-04-23 4437
-
哪位大神会用matlab设计butterworth滤波器程序,急求帮助!2013-09-10 3118
-
【WEBENCH 大赛作品】基于OPA656的四阶Butterworth低通滤波器电路2015-07-22 2702
-
滤波器自身波形显示2017-03-26 2270
-
频率滤波器怎么分类?2019-09-19 3109
-
巴特沃斯滤波器与切比雪夫滤波器有什么不一样?2019-10-14 3783
-
IIR滤波器的设计与性能分析2009-05-10 1908
-
滤波器设计的概念2010-03-29 1647
-
高阶Butterworth低通滤波电路的快速设计2010-05-05 594
-
无线通信用SAW滤波器的分析与设计详解2017-08-30 1093
-
多路反馈型带阻滤波器设计研究2017-11-22 3957
-
一阶有源滤波器原理详解2022-11-14 3722
-
二阶有源高通滤波器原理详解2022-11-18 5113
-
二阶有源带通滤波器原理详解2022-11-21 5683
-
Chebyshev滤波器设计的详解2023-02-20 18487
全部0条评论

快来发表一下你的评论吧 !

