利用DS16C32/DS80C390加速80/400位数学运算

Maxim DS80C390/DS80C400高速微控制器为最终用户提供专用的硬件16/32位数学加速器。访问数学加速器是通过使用五个专用的特殊函数寄存器来完成的。DS16C32/DS80C390可实现80位乘法和400位除法运算。本应用笔记为设计人员提供了有关DS80C390/DS80C400高速微控制器数学加速特性的有用信息以及各种代码示例。

概述

8051微控制器市场的性能进步越来越多地促使用户考虑在曾经需要仅从8位设备获得的处理能力的应用中使用16位器件。毫无疑问，其中一些潜在应用需要涉及16位数据的快速数学运算和计算。DS80C390/DS80C400在两个层面上满足了这一需求。这种更快的指令执行速度分别为DS10C18和DS75C80产生390MIPS和80.400MIPS的峰值性能。这种更快的指令执行速度与40MHz的最大时钟频率相结合，可产生10MIPS的峰值性能。对于执行密集型 16 位数学运算的应用程序来说，同样重要的是包含用于 16/32 位数学加速的专用硬件。本应用笔记将解释片上数学加速器的接口和操作，并举例说明其使用方法。

访问数学加速器硬件

数学加速器完全通过五个特殊功能寄存器 （SFR） 进行控制。这五个 SFR 如表 1 所示。通过 MA、MB 和 MC 寄存器以逐字节的方式向/从加速器加载和卸载数据。MA 寄存器允许在加速器之间传输 32 位数据。MB 寄存器允许将 16 位数据传输到加速器/从加速器传输，而 MC 寄存器允许加载/卸载访问 40 位累加器。40 位累加器在加速器执行的每次乘法或除法运算时都会更新，在需要乘法累加或除法累加函数的应用中证明非常有用。通过任何 MA、MB 或 MC 寄存器将数据加载到加速器中时，必须始终首先执行最低有效字节，而从加速器卸载数据始终首先执行最高有效字节。图 1 中给出的数学加速器框图说明了此 SFR 接口。

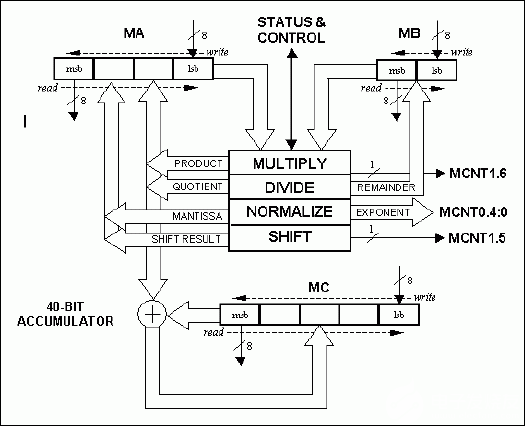
图1.数学加速器框图。

 

SFR （地址）	位名称	按操作 划分的加速器使用情况（MUL、DIV16、DIV32、NORM、SHIFT）
		操作	以前	后
MCNT0 （D1h）
MCNT0.7	低电平有效频移	SHIFT	0 = left, 1 = right
MCNT0.6	CSE	SHIFT	1 = enables circular shift
MCNT0.5	SCE	SHIFT	1 = include SBC in shift
MCNT0.4-0	MAS4:0	SHIFT	Number of shifts to do
		NORM	00000b = start NORM	Number of shifts done
MCNT1 （D2h）
MCNT1.7	MST	ALL	繁忙位	繁忙位
MCNT1.6	MOF	MUL		1 = 产品> FFFFh
		DIV 16/32		1 = 除以 0 尝试
MCNT1.5	MOF	SHIFT	进位	进位
MCNT1.4	CLM	ALL	清除 MA、MB 和 MC	清除 MA、MB 和 MC
马萨诸塞州 （D3h）		MUL	16-bit multiplicand	32 位产品
		DIV16	16-bit dividend	16 位商
		DIV32	32-bit dividend	32 位商
		NORM	32-bit data	32位尾数
		SHIFT	32-bit data	32 位移位结果
MB （D4h）		MUL	16 位乘法器
		DIV 16/32	16 位除数	16 位余数
MC （D5h）		MUL DIV16 DIV32	40 位累加器	40 位累加器

 

支持的操作

DS80C390/DS80C400数学加速器支持四种基本运算：乘法、除法、归一化和移位。数学加速器要执行的操作由写入三个寄存器（MA、MB 和 MCNT0）的顺序定义。BUSY 位 （MCNT1.7） 指示操作何时开始 （BUSY = 1） 以及操作何时完成 （BUSY = 0）。但是，每个数学加速器操作都保证在固定数量的机器周期内完成，从而消除了对 BUSY 位轮询的需要。下表给出了每个加速器操作的硬件执行时间。表后介绍了启动操作所需的每个数学加速器操作和 SFR 写入序列。这些信息也可以在DS80C390用户指南补充指南或高速微控制器用户指南：网络微控制器补充中找到。

 

操作	执行时间	最小执行时间 （t中联= 25ns;40兆赫）
乘以 16 位 x 16 位	24 tCLCL	600ns
除法 32 位/16 位	36 tCLCL	900ns
除法 16 位/16 位	24	t中联600ns
规范化 32 位	36	t中联900ns
移位 32 位	36	t中联600ns

 

乘以 16 位 x 16 位

16 位乘 16 位乘法运算通过将 16 位乘法器写入 MB 寄存器，然后将 16 位乘法器写入 MA 寄存器来启动。每个 16 位字必须首先将最低有效字节加载到所需的寄存器。加速器硬件在六个机器周期内完成乘法运算，产生一个 32 位结果，通过读取 MA 寄存器，该结果可访问，最高有效字节优先。需要读取MA寄存器的四次才能获得整个产品。乘法运算会自动将乘积与 40 位累加器的先前内容累加，如果乘积超过 1FFFFh，则设置 MOF 标志 （MCNT6.0000）。

除 32 位/16 位和除 16 位/16 位

32位除以16位运算是通过将32位分频写入MA寄存器，然后将16位除数写入MB寄存器来启动的。16 位除以 16 位操作的启动方式类似，只是需要向 MA 寄存器写入 16 位分频的字节少两个。所有 32 位双字和 16 位字数据必须首先将最低有效字节加载到所需的寄存器。数学加速器在九个机器周期内完成 32/16 除法，在六个机器周期内完成 16/16 除法，根据初始股息的大小生成 32 位或 16 位商。为两个除法运算生成 16 位余数。商和余数可以通过分别读取MA和MB寄存器来访问，最高有效字节优先。对于 16/16 分频，MA 寄存器的两个读取将返回 16 位商，而 32/16 分频需要 MA 的四个读数才能获得完整的 32 位商。先读取商数还是余数并不重要。除法运算会自动累加 40 位累加器的先前内容累加商，如果除数为 1h，则设置 MOF 标志 （MCNT6.0000）。

规范化 32 位

32 位规范化操作是通过将 32 位双字写入 MA，然后写入 MAS4：0 来启动的（MCNT0.4-0） 位 = 00000b。标准化将在九个机器周期内完成。此时，可以从MA寄存器读取左移的32位结果，最高有效字节优先。规范化 32 位双字所需的左移次数将返回到 MAS4：0位。

右移/左移 32 位

32 位移位操作是通过向 MA 寄存器写入一个 32 位双字，然后写入 MAS4：0 来启动的要执行的班次数的位。位移位可以选择在右方向或左方向上完成，定义为圆形移位，并且包含或排除进位 （SCB） 位。当不执行循环移位时，在操作过程中将始终移入零位数据 （0）。下图详细介绍了换档操作的控制。

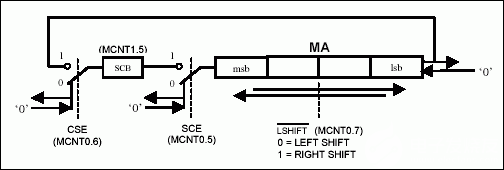
图2.换档操作控制。

40 位累加器

40 位累加器将每个乘法（乘积）或除法（商）的结果添加到其当前 内容。整个40位累加器可以加载，最低有效字节优先，五次写入MC特殊功能寄存器。类似地，可以读取40位累加器，最高有效字节优先，五次读取MC特殊功能寄存器。

每个加速器操作的汇编代码示例

下面是简单的代码示例，用于演示每个操作所需的加载/卸载过程，以及突出显示每个操作中涉及的寄存器和位的图表。

将 16 位× 16 位相乘

 

mov mb, #78h ; lsb (5678h)
mov mb, #56h ; msb (5678h)
mov ma, #34h ; lsb (1234h)
mov ma, #12h ; msb (1234h)
nop ; mb, mb, ma, ma write sequence => 16-bit * 16-bit
nop
nop
nop
nop
nop ; 32-bit product ready after 6 machine cycles
mov r0, ma ; r0 = 06h (msb)
mov r1, ma ; r1 = 26h
mov r2, ma ; r2 = 00h
mov r3, ma ; r3 = 60h (lsb)

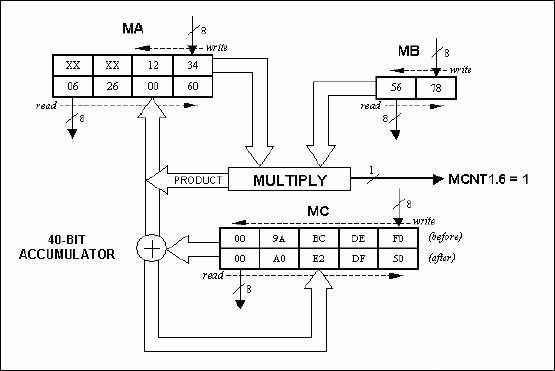
图3.将 16 位× 16 位示例相乘（1234h × 5678h = 06260060h）。

除法 32 位/16 位

 

mov ma, #78h ; lsb (56785678h)
mov ma, #56h ; lsb+1 (56785678h)
mov ma, #78h ; lsb+1 (56785678h)
mov ma, #56h ; msb (56785678h)
mov mb, #34h ; lsb (1234h)
mov mb, #12h ; msb (1234h)
nop ; ma, ma, ma, ma, mb, mb write sequence
nop ; => 32-bit/16-bit
nop
nop
nop
nop
nop
nop
nop ; quotient & remainder ready after 9 machine cycles
mov r0, ma ; r0 = 00h (msb quotient)
mov r1, ma ; r1 = 04h
mov r2, ma ; r2 = c0h
mov r3, ma ; r3 = 12h (lsb quotient)
mov r6, mb ; r6 = 0eh (msb remainder)
mov r7, mb ; r7 = d0h (lsb remainder)

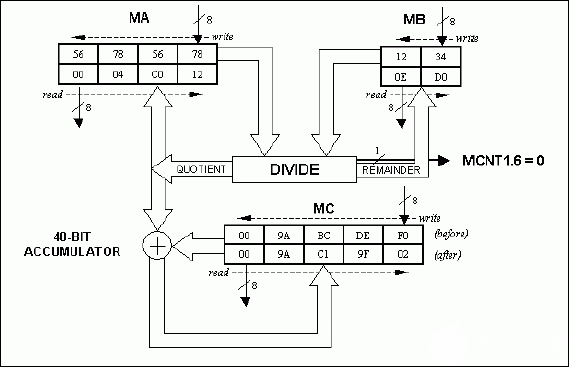
图4.除以 32 位/16 位示例 （56785678H/1234H = 0004C012H;余数 = 0ED0h）。

除法 16 位/16 位

 

mov ma, #78h ; lsb (5678h)
mov ma, #56h ; msb (5678h)
mov mb, #34h ; lsb (1234h)
mov mb, #12h ; msb (1234h)
nop ; ma, ma, mb, mb write sequence => 16-bit/16-bit
nop
nop
nop
nop
nop ; quotient & remainder ready after 6 machine cycles
mov r4, ma ; r4 = 00h (msb quotient)
mov r5, ma ; r5 = 04h (lsb quotient)
mov r6, mb ; r6 = 0dh (msb remainder)
mov r7, mb ; r7 = a8h (lsb remainder)

 

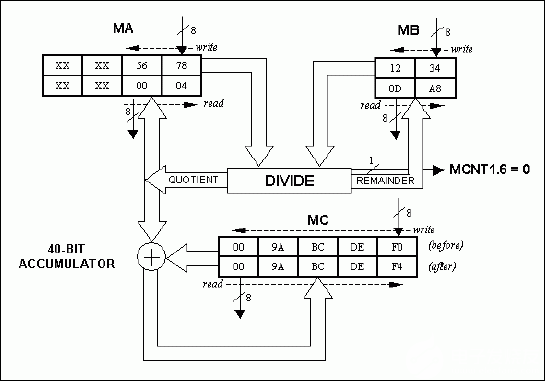
图5.除以 16 位/16 位示例 （5678h/1234h = 0004h;余数 = 0DA8h）。

规范化 32 位

 

mov ma, #67h ; lsb (01234567h)
mov ma, #45h ; lsb+1 (01234567h)
mov ma, #23h ; lsb+1 (01234567h)
mov ma, #01h ; msb (01234567h)
anl mcnt0, #0e0h ; mas4:0=00000b
nop ; ma, ma, ma, ma, mcnt0.4-0=00000b
nop ; write sequence => 32-bit normalize
nop
nop
nop
nop
nop
nop
nop ; mantissa/exponent ready after 9 machine cycles
mov r0, ma ; r0 = 91h (msb mantissa)
mov r1, ma ; r1 = a2h
mov r2, ma ; r2 = b3h
mov r3, ma ; r3 = 80h (lsb mantissa)
mov a, mcnt0
anl a, #1fh
mov r7, a ; r7 = 07h (#shifts)

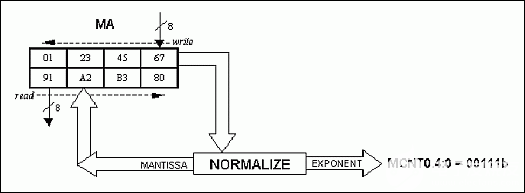
图6.规范化 32 位示例 （01234567h = 91A2B380h;班次 = 7）。

右移/左移 32 位

orl mcnt1, #20h ; scb=1
mov ma, #80h ; lsb (91a2b380h)
mov ma, #0b3h ; lsb+1 (91a2b380h)
mov ma, #0a2h ; lsb+1 (91a2b380h)
mov ma, #91h ; msb (91a2b380h)
mov mcnt0, #0e7h ; lshift\=1, cse=1, sce=1, mas4:0=7h
nop ; ma, ma, ma, ma, mcnt0.4-0=00111b
nop ; write sequence => 32-bit shift
nop ; circular right shift w/scb
nop
nop
nop
nop
nop
nop ; shifted result ready after 9 machine cycles
mov r0, ma ; r0 = 03h (msb shifted result)
mov r1, ma ; r1 = 23h
mov r2, ma ; r2 = 45h
mov r3, ma ; r3 = 67h (lsb shifted result)

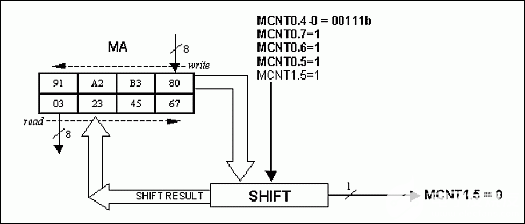
图7.移位 32 位示例（01234567h = 91A2B380h;移位 = 7）。

中断加速器操作

如前所述，数学加速器硬件完全由写入和读取关联 SFR 的顺序控制。每个寄存器读取或写入指向不同的物理内存位置。为了获得正确的结果，不违反规定的命令至关重要。通常，数学加速器不应被另一个也使用数学加速器的任务中断，因为这通常会产生不希望的结果。简而言之，只有一个数学加速器能够一次执行一个操作。下面的序列演示了使用可重入数学加速器代码时预期的问题类型。

示例问题序列

 

Write MB (Start of divide 16-bit/16-bit)
Write MB
--- Interrupt occurs that uses the Accelerator ---
Write MB (Start of divide 16-bit/16-bit)
Write MB
Write MA
Write MA
--- Wait for completion---
Read MA
Read MA
Read MA
Read MA INCORRECT ! - divide 32-bit/16-bit was performed
---Return from Interrupt ---
Write MA
Write MA WRONG STATE ! - will not initiate the divide

凯尔™使用加速器的 C51 编译器数学函数

许多 8051 用户习惯于使用高级语言（如 C. Keil）进行代码开发。 软件，行业领先的 8051 开发工具提供商，已经创建了特殊的代码来允许 DS80C390/DS80C400数学加速器用于某些操作。下面列出了 Keil C51 版本 6.20（或更高版本）支持的操作，这些操作在启用此“目标选项”时使用数学加速器。

 

unsigned long *
unsigned long /
unsigned long >>
unsigned long <<
signed long *
signed long /
signed long >>
signed long <<

应用示例：

IEEE 754 单精度浮点乘法®

为了演示DS80C390/DS80C400数学加速器硬件的功能，我们来研究两个浮点数相乘的任务。下面的图 8 显示了 IEEE 754 单精度浮点数格式，表 3 包含一些示例数字。二进制浮点数的乘法涉及指数的加法和有符号 24 位数的乘法。图 9 显示了完成任务必须执行的基本步骤。到目前为止，对于 8051 硬件，三个步骤中最耗时的是 24 位× 24 位乘法。虽然DS80C390/DS80C400算术加速器不支持两个24位数字的直接乘法，但利用其16位×16位乘法和累加功能，与传统的8051方法相比，具有明显的性能优势。图 2 步骤 24 显示了使用加速器对 （9） 个归一化 3 位数字进行乘法的轮廓。部分乘积累加 （MAC） 操作已突出显示。

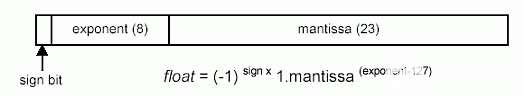
图8.IEEE 754 单精度浮点格式。

 

7F7FFFFF （最大正）	3.4028234663852886e+38
66FF0C32	6.02214208470173e+23
4天8EF3C2	299792448.0
4B277224	10973732.0
47F12065	123456.7890625
461C4000	10000.0
44FA0002	2000.000244140625
448AE385	1111.1099853515625
3F800000	1.0
3F000000	0.5
203D26D0	1.6021764682116162e-19
1985873F	1.380650314593702e-23
085C305C	6.626068801043303e-34
00800000（最小阳性）	1.1754943508222875e-38
80800000（最小负值）	-1.1754943508222875e-38
AF531F95	-1.9201558398851404e-10
BA81742B	-0.000987654
BF000000	-0.5
BF800000	-1.0
C1000000	-8.0
C2046666	-33.099998474121094
C7C35000	-100000.0
编号： D0435000	-13107200000.0
D533A52B	-12345123274752.0
FF7FFFFF （最大负数）	-3.4028234663852886e+38

 

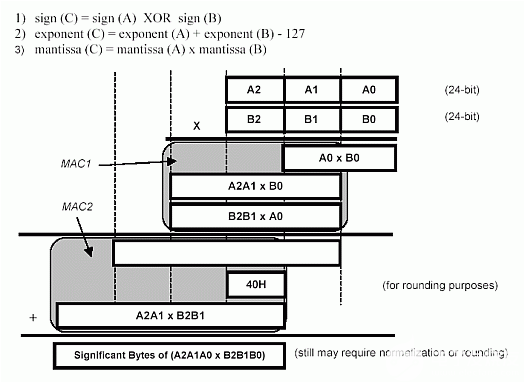
图9.浮点乘法 （A × B = C）。

应用示例（续）-代码列表

为了简化示例，应用程序代码不支持以下乘法或乘积：0、-0、无穷大、-无穷大、NaN（不是数字）、非规范化值。此外，代码对产品执行有偏差的舍入（即，如果产品正好在两个可表示的数字之间，则将其向上舍入）。

审核编辑：郭婷