

“缝合”摆脱逻辑分析仪内存限制
描述
MATLAB 是一款功能强大的工具,可用于快速分析从模数转换器 (ADC) 输出捕获的数据。本应用笔记演示了如何使用MATLAB来避免逻辑分析仪存储器深度的限制。描述并比较了三种代码切换方法(基本、高级和反向)。给出了所有三种方法的结果。
介绍
检定高速模数转换器(ADC)需要捕获和分析数字输出代码。逻辑分析仪存储器深度的限制经常妨碍捕获足够的数据点来创建高分辨率FFT或INL/DNL图形的精确表示。规避此问题的一种简单方法是使用 MATLAB 等数学工具连接多组数据(图 1)。连接数据的一个缺点是较大的不连续性,这通常存在于两个数据集之间的点。虽然不连续性对 INL/DNL 图几乎没有影响,但它会对高分辨率 FFT 造成严重破坏(图 2)。
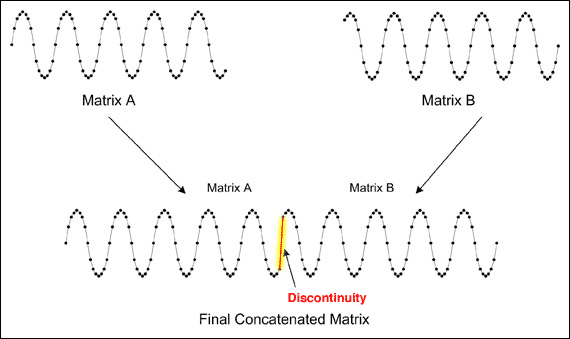
图1.串联数据揭示了两个数据集之间的不连续性。
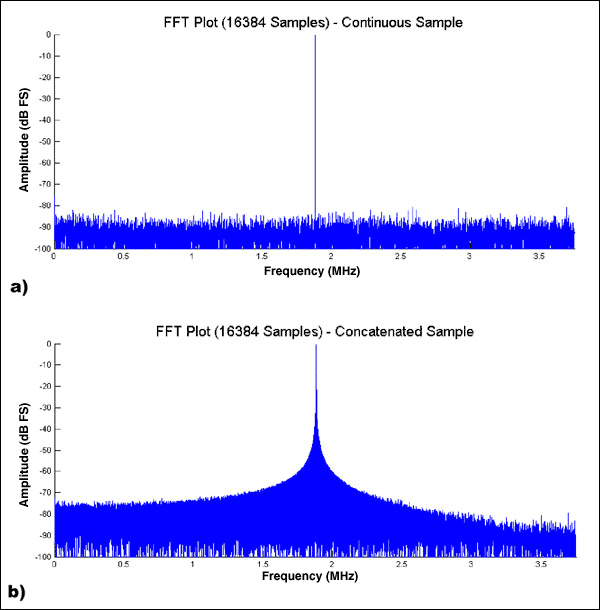
图2.a) 捕获并分析了单个 16384 点数据集;b) 捕获、连接和分析了两个 8192 点数据集。缝合技术。
可以通过在每个数据集中搜索相同的点组(通常为三个或四个)并在这些点处将两个数据集“拼接”在一起来消除不连续性(图 3)。完成此拼接的最简单方法是记录第一个数据集中的最后四个点,然后在第二个数据集中搜索一组相同的点。第二个数据集中的这个位置称为“缝合点”。第二个数据集中此拼接点之前的任何数据都将被丢弃;第二个数据集的其余部分附加到第一个数据集。这种技术称为基本代码拼接,实现起来相当简单,并且在 MATLAB 中执行速度非常快。
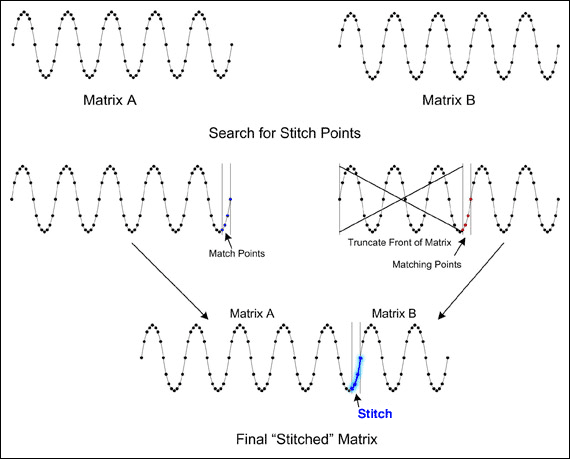
图3.基本代码拼接会产生最终的“拼接”矩阵。
使用基本代码拼接,有时需要丢弃多达一半的第二个数据集,以便找到与第一个数据集的最后四个点匹配的一组点。或者,在第一个数据集的末尾丢弃一些样本通常有助于找到更接近第二个数据集开头的拼接点(图 4)。但是,寻找从第一个数据集的尾端和第二个数据集的前端丢弃样本的匹配可能很难实现。此过程称为高级代码拼接。找到产生最大结果数据集的理想拼接点需要相当深思熟虑和编程技能。但是,如果实施得当,高级代码拼接通常会产生一个最终数据集,该数据集至少是两个较小数据集之和的 90%。
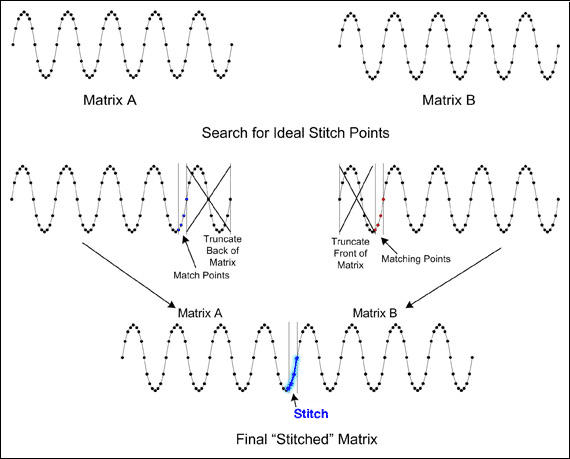
图4.高级代码拼接寻找理想的拼接点,从而产生最终的“拼接”矩阵。
将第二个数据集(矩阵B)拼接在第一个数据集(矩阵A)前面称为反向代码拼接,也可能产生更大的数据集(图5)。然而,这种技术使处理时间加倍,因为当数据集 A 在数据集 B 之前,当数据集 A 在数据集 B 之后时,必须找到拼接点。此外,反向代码拼接与其他拼接技术结合使用时通常产生最小的收益。因此,由于反向代码拼接所需的处理时间大幅增加,在速度较慢的PC上,额外的代码增益可能不合理。表 1 详细介绍了三种代码拼接方法之间的比较。
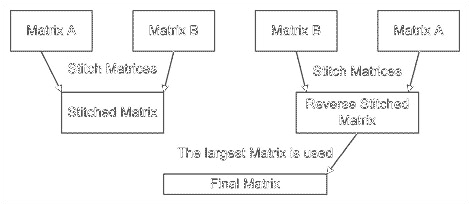
图5.反向代码拼接使处理时间加倍,通常代码增益最小。
| 缝合技术 | 最终数据集的大小 | 描述 | ||||
| 数据集编号 |
# 代码 (平均) |
两个数据集 的百分比(平均值) |
||||
| 1 + 2 | 3 + 4 | 1 + 4 | ||||
| 连接† | 不适用 | 16384 | 100% | 会产生错误的FFT;但是,可以从这些数据中提取INL/DNL。 | ||
| 基本 | 11060 | 8192‡ | 14384 | 11212 | 68.4% | FFT可用于计算品质因数。 |
| 反向 | 11060 | 8192‡ | 14384 | 11212 | 68.4% | |
| 高深 | 13790 | 16046 | 16022 | 15286 | 93.3% | |
|
高级 + 反向 |
15427 | 16176 | 16022 | 15875 | 96.9% | |
|
*使用上述技术将两个 8K(8192 代码)数据集拼接在一起。为了确保准确性,使用四组8192点数据(标记为1到4)重复测试三次。对每个测试的结果数据进行平均,并显示在测试数据的右侧。 †串联始终产生 100% 的可用数据。 ‡无法将数据集拼接在一起。 |
||||||
MATLAB 功能说明
附加的 MATLAB 代码(附录 A 和 B 中的 StitchMatrices 和 FindStitchPoint)将上述主题组合成一个易于使用的函数。这些函数接受两个数据集(MATLAB 中的单列矩阵)和多个启用高级/反向代码拼接功能的输入参数。FindStitchPoint 例程标识数据集 A 和 B 中的偏移量。StitchMatrices 例程丢弃数据集 A 和 B 并使用 FindStitchPoint 例程中的偏移量将数据集 A 和 B 组合在一起。此外,最终数据集中的针迹点记录在PrevStitchBins矩阵中以进行后处理。将多个数据集拼接在一起时,PrevStitchBins会保留旧拼接点的位置。
结论
将两组数据拼接在一起可以产生可接受的结果。图 6 描述了使用上述拼接技术拼接在一起的三个 8192 点数据集(使用五个拼接点)的 FFT 图。得到的FFT与上面图16384a所示的2点连续数据集几乎相同。
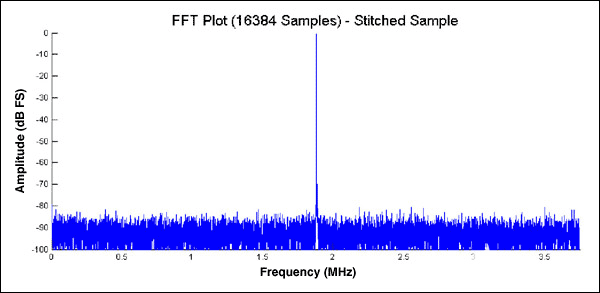
图6.将代码拼接在一起可产生精确的FFT图。
审核编辑:郭婷
-
逻辑分析仪是干啥用的 逻辑分析仪的主要用途 逻辑分析仪的应用场景2023-09-19 5055
-
安捷伦科技逻辑分析仪推出最深的内存2019-10-14 1271
-
逻辑分析仪探头的物理形式2019-08-28 4174
-
逻辑分析仪的作用_逻辑分析仪怎么用_逻辑分析仪的使用方法(教程)2017-12-20 55262
-
浅谈逻辑分析仪2017-08-09 1172
-
逻辑分析仪基础简介2017-08-07 3058
-
逻辑分析仪是什么2016-08-23 3648
-
逻辑分析仪使用手册 (1)2016-05-13 1032
-
逻辑分析仪基础指南2010-08-05 725
-
逻辑分析仪的使用2008-11-27 2797
全部0条评论

快来发表一下你的评论吧 !

