

综述:特征点检测与匹配
描述
导读
本文先从图像特征开始介绍,后分点阐述特征子和描述子的相关分类及特点,最后以图像展示了特征匹配的关系,完整的叙述了整个建模过程中特征点检测与匹配的知识。
一、图像特征介绍
1、图像特征点的应用
- 相机标定:棋盘格角点阴影格式固定,不同视角检测到点可以得到匹配结果,标定相机内参
- 图像拼接:不同视角匹配恢复相机姿态
- 稠密重建:间接使用特征点作为种子点扩散匹配得到稠密点云
- 场景理解:词袋方法,特征点为中心生成关键词袋(关键特征)进行场景识别

2、图像特征点的检测方法
- 人工设计检测算法:sift、surf、orb、fast、hog
- 基于深度学习的方法:人脸关键点检测、3D match点云匹配
- 场景中的人工标记点:影视场景背景简单的标记,特殊二维码设计(快速,精度低)

3、图像特征点的基本要求
- 差异性:视觉上场景上比较显著点,灰度变化明显,边缘点等
- 重复性:同一个特征在不同视角中重复出现,旋转、光度、尺度不变性

二、特征检测子
1、Harris 角点检测(早期,原理简单,视频跟踪,快速检测)
梦寐mayshine:角点检测(2) - harris算子 - 理论与Python代码
https://zhuanlan.zhihu.com/p/90393907

- 动机:特征点具有局部差异性
- 以每个点为中心取一个窗口,例如,5×5/7×7的像素,描述特征点周围环境
- 此点具有差异性->窗口往任意方向移动,则周围环境变化较大->具有局部差异性
- 最小二乘线性系统
- 加和符号:表示窗口内每个像素
- w:表示权重,权值1或者以点为中心的高斯权重(离点越近权重越大)
- I:表示像素,RGB/灰度
- u,v:窗口移动的方向
- H:harris矩阵,由两个方向上的梯度构建而成
- 图像梯度:
- Harris矩阵:
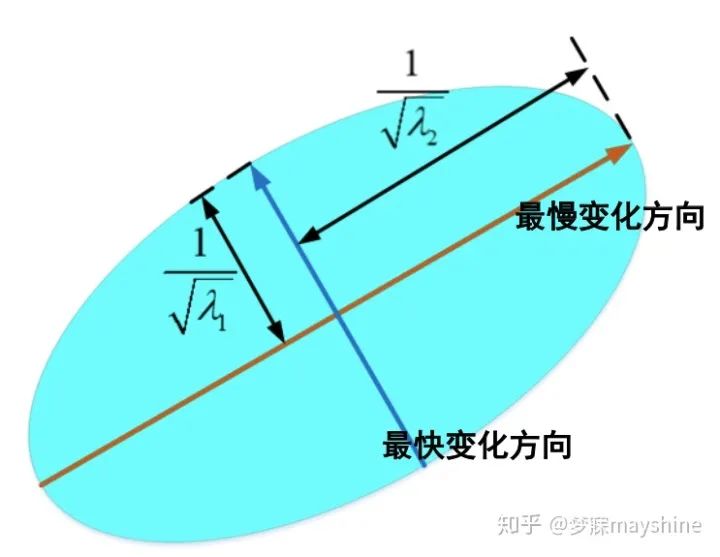
- Harris矩阵H 的特征值分析
- 两个特征值反映相互垂直方向上的变化情况,分别代表变化最快和最慢的方向,特征值大变化快,特征值小变化慢
- λ1 ≈ λ2 ≈ 0, 两个方向上变化都很小,兴趣点位于光滑区域
- λ1 > 0 , λ2 ≈ 0 ,一个方向变化快,一个方向变化慢,兴趣点位于边缘区域
- λ1 , λ2 > 0 , 两个方向变化都很快,兴趣点位于角点区域(容易判断)
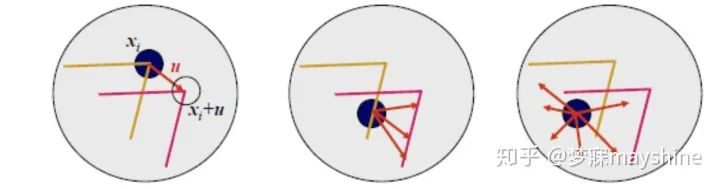
- Harris角点准则代替矩阵分解:
- 反映特征值情况,trace为迹
- k的值越小,检测子越敏感
- 只有当λ1和λ2同时取得最大值时,C才能取得较大值
- 避免了特征值分解,提高检测计算效率
- 非极大值抑制(Non-maximal Suppression) 选取局部响应最大值,避免重复的检测
- 算法流程:
- 0)滤波、平滑,避免出现阶跃函数
- 1)计算图像水平和垂直方向的梯度
- 2)计算每个像素位置的Harris矩阵
- 3)计算每个像素位置的Harris角点响应值
- 3+)非极大值抑制
- 4)找到Harris角点响应值大于给定阈值且局部最大的位置作为特征点
- 检测结果:

2、基于LoG的多尺度特征检测子
- 动机:Harris角点检测不具有尺度不变性,让特征点具有尺度不变性

- 解决方法:尺度归一化LoG算子,处理尺度的变化
- LoG算子:Lindeberg(1993)提出Laplacian of Gaussian (LoG)函数的极值点对应着特征点
- 尺度空间: 一副图像使用不同大小滤波核滤波(e.g.高斯滤波),越大的滤波核越模糊,分辨率越小,不同滤波核滤波后的空间为尺度空间=3维空间(图像+尺度),模拟人类视觉,较远物体模糊,一系列滤波核构成的不同分辨率图像为尺度空间->LoG能够处理不同尺度的图像

- LoG算子[1]形式:高斯滤波性质:卷积->求拉普拉斯算子==求拉普拉斯算子->卷积 其中 是LoG算子
- 尺度归一化LoG[2](使得具有可比性=汇率):其中 是尺度归一化LoG算子
- 不同尺度下的LoG响应值不具有可比性
- 构建尺度空间,同时在位置空间和 尺度空间寻找归一化LoG极值(极大 /极小)点作为特征点
- 不同尺度下 的响应值
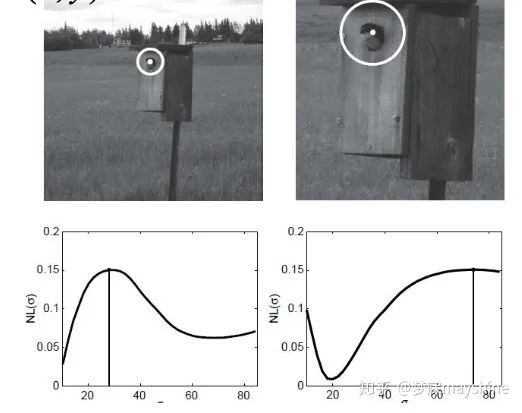
- LoG特征检测算法流程
- 1)计算不同尺度上的尺度归一化LoG函数值
- 2)同时在位置和尺度构成的三维空间上寻找 尺度归一化LoG的极值点
- 3)进行非极大值抑制,减少重复检测 (去除冗余、保持稳定性)
- 检测结果:效果好,LoG计算量大

3、基于DoG的多尺度特征检测子(SIFT)——稳定和鲁棒
- LoG可以由DoG近似:Lowe(2004)提出归一化LoG近似等价于相邻尺度的高斯差分(DoG)
- 高斯空间:
- 高斯差分DoG:相邻的空间做差,极点处对应特征点
-
尺度空间的构建
- 阶数:O=3 (octave=阶,每阶图像尺寸减少一半,阶数高->运算量大->尺度变化大)
- 每阶有效差分数:S=3(每个阶内划分数)
- 每阶层数:N=S+3
-
高斯空间
-
高斯差分
-
有效差分 (尺度空间有上下两个邻域才行,边界无效)
-
任意设置
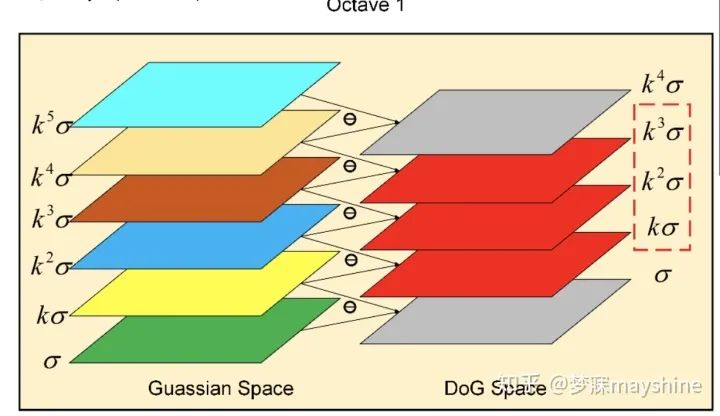
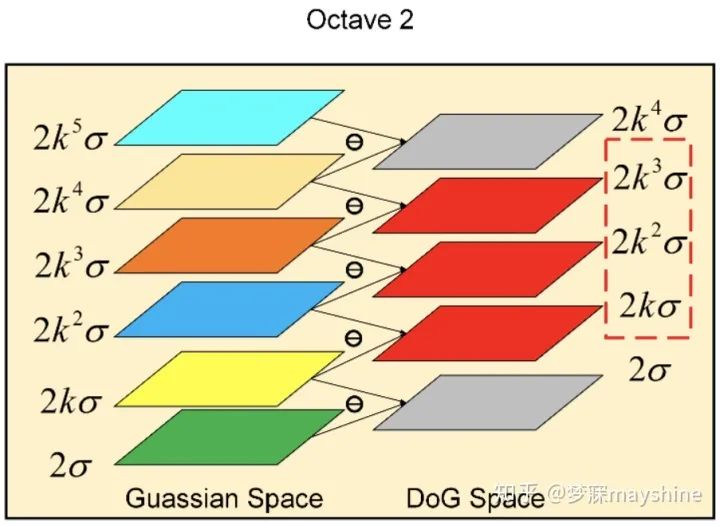
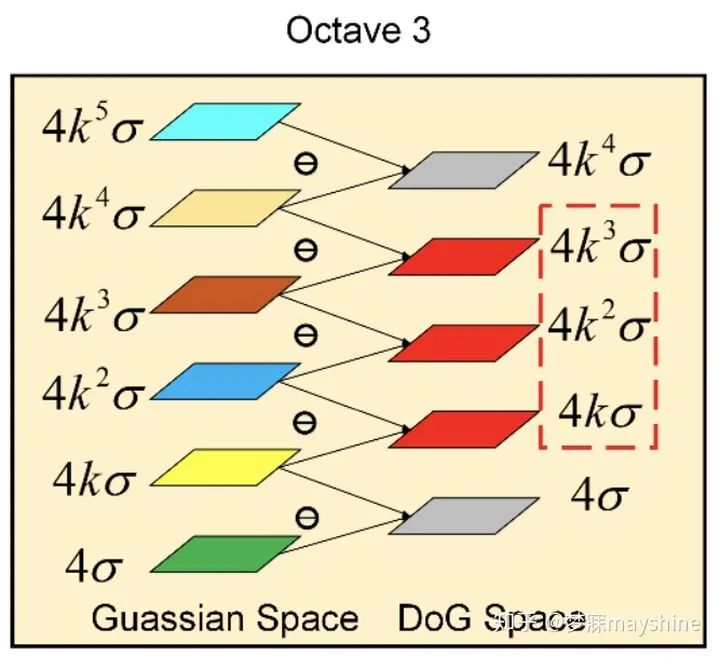
- 特征点位置的确定:
- 1)尺度空间和图像空间上:3*3窗口,26个邻域,找极值点比其他都要大DoG,LoG找极大值或极小值
- 2)横轴向代表离散位置,纵轴代表DoG响应值,在极值点邻域内求二阶函数的极值=准确像素位置
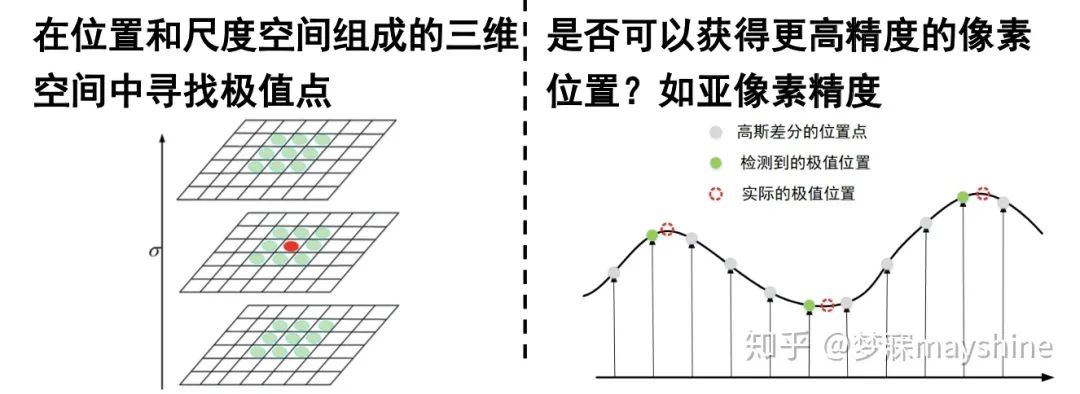
-
亚像素特征点位置的确定
- x: 为三维,坐标空间+尺度空间
- f(x): 为DoG值
- x0: 检测到离散坐标下的极大值点
- 任务:在x0附近近似一个二阶函数,求二阶函数极值得到更准确的亚像素极值位置

- 矩阵的表达-1阶

- 矩阵的表达-2阶
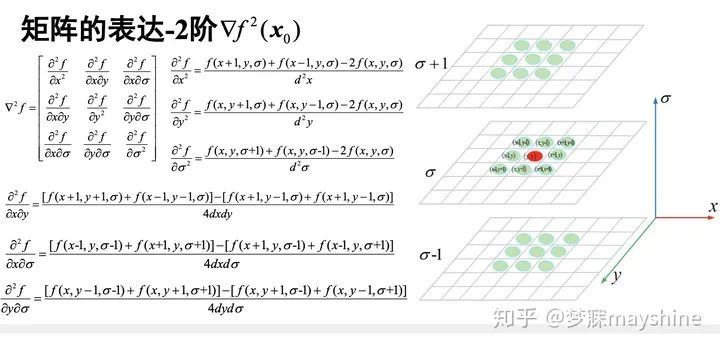
- 极值点有可能是边缘点,->除去边缘点:DoG在边缘处值较大,需要避免检测到边缘点
- 计算主方向:通过统计梯度直方图的方法确定主方向,使算法具有旋转不变性
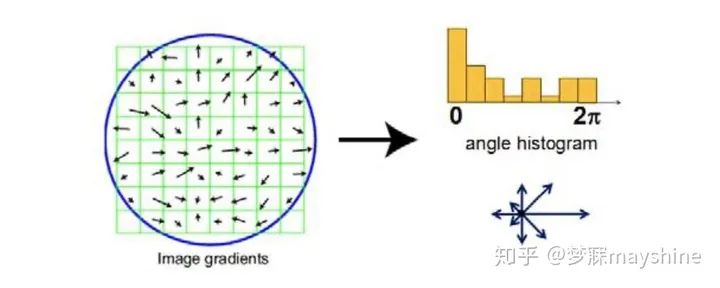
-
SIFT特征检测流程:旋转不变性、尺度不变性、亮度 变化不变性,对视角变化、仿射变换有一定程度的稳定性
- 1)计算图像尺度空间:
- 2)DoG极值点检测与定位:保留 的特征点
- 3)边缘点去除:
- 4)计算主方向
- 5)生成描述子
- 6)检测结果

4、快速特征点检测方法:——实时性要求高
-
FAST特征点[3]:Feature from Accelerated Segment Test
- 1)以候选点p为圆心构建一个离散圆
- 2)比较圆周上的像素与p点像素值
- 3)当有连续的n个像素值明显亮于或者暗于p时,p被检测为特征点,例Fast9,Fast12
-
特性:通过检测局部像素灰度变化来确认特征点的位置,速度快,SIFT的100倍;不具有尺度和旋转不变性
-
流程:
-
检测:

-
Oriented FAST (ORB)
- 获取尺度不变性:构建图像金字塔,在金字塔 每一层上检测关键点
- 获取旋转不变性 :通过灰度质心法(Intensity Centroid) 确定图像主方向
- 图像块B上的矩定义为:
- 图像块B的质心定义为 :
- 计算方向角 :
- 检测结果:

三、特征描述子
特征描述子 Feature Descriptor
- 每个特征点独特的身份认证
- 同一空间点在不同视角的特征点具有高度相似的描述子
- 不同特征点的的描述子差异性尽量大
- 通常描述子是一个具有固定长度的向量
特征支持区域
- 主方向:进行旋转并重新插值
- 特征尺度:影响支持区域的大小
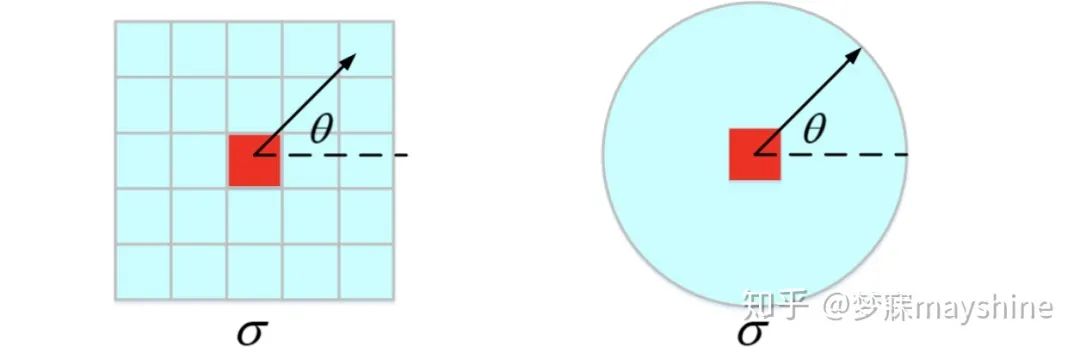
1、基于直方图的描述子
(1)用于微小运动的描述子 [4](e.g.相邻两帧视频)
- 定义:以特征点为中心的矩形区域内所有像素的灰度值作为描述子
- 特性:适用于微小变化的图像对 图像存在明显的旋转、尺度、光照和透视变换时不稳定
(2)Sift描述子——旋转主方向
- 定义:根据主方向对支持区域进行旋转,并通过双线性插值重构
- 特性:图像归一化处理,去除光照变化

-
统计局部梯度信息流程:
- 1)将区域划分成4x4的block ;
- 2)每个block内统计梯度方向 的直方图(高斯加权梯度作为系数)
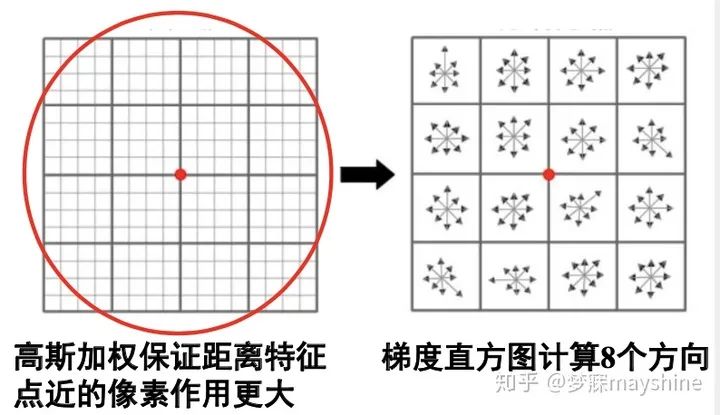
(2)Sift描述子——生成描述子
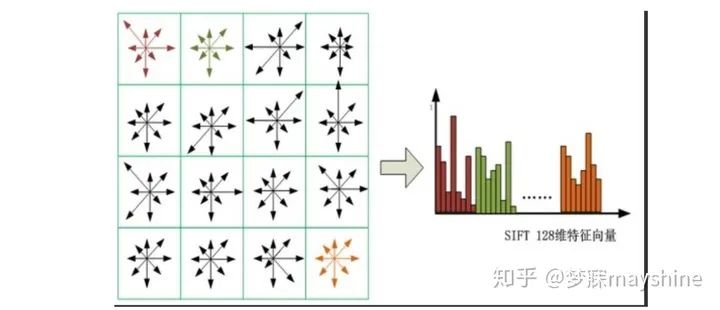
(2)Sift描述子——归一化处理
-
处理方式
- 1)门限处理-直方图每个方向的梯度幅值不超过0.2
- 2)描述子长度归一化
-
特性:归一化处理提升了特征点光度变化的不变性
-
SIFT描述子变种:PCA-SIFT/SURF
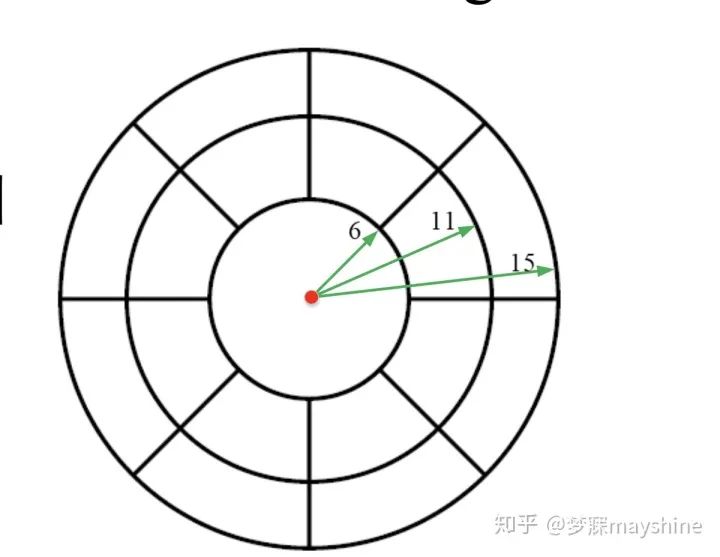
(3)GLOH描述子[5]:Gradient Location-orientation Histogram
- 一共有1+2x8=17 个blocks
- 每个blocks计算16个方向的直方图
- 描述子共16x17=272维
- 通过PCA可以降维到128
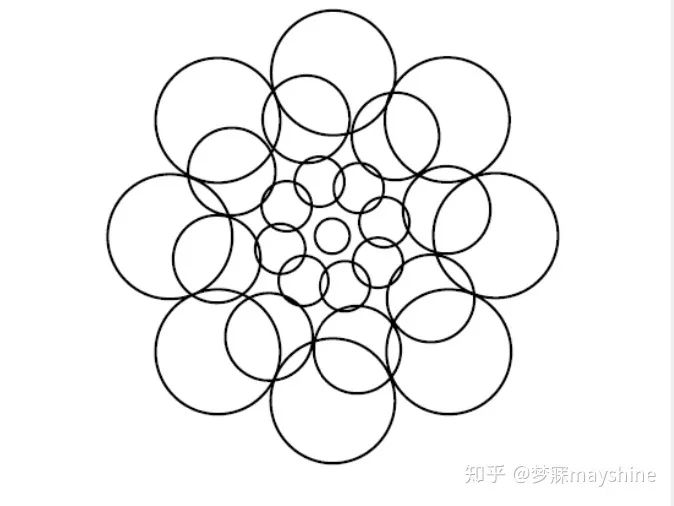
(4)DAISY描述子[6]:每个圆的半径对应高斯的尺度
2、基于不变性的描述子
3、二进制描述子——BRIEF
-
描述子形式:描述向量由N个0或者1组成 N=128,256,512
-
描述子特性:生成速度快(汉明距离),匹配效率高 ,简单有效;不具有旋转不变性
-
描述子流程:
- 1)图像进行如高斯滤波预处理——去除噪声
- 2)在支持区域内随机采样N对大小5×5的patch
-
3)比较patch内像素和的大小,并保留结果构成特征向量 $ au(p;x,y)=left{ egin{aligned} 1, ifp(x)

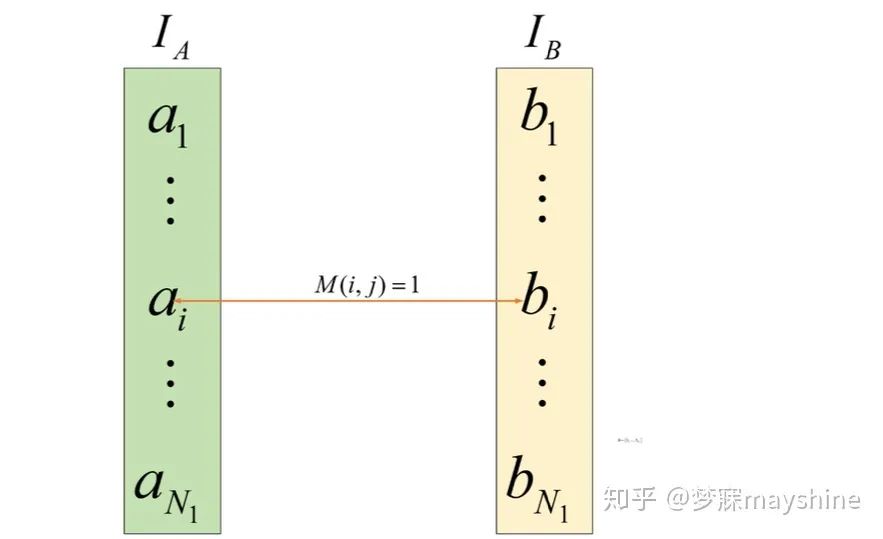
四、特征匹配
计算两幅图像中特征描述子的匹配关系
1、距离度量
归一化互相关,1 ->非常匹配,0->不匹配
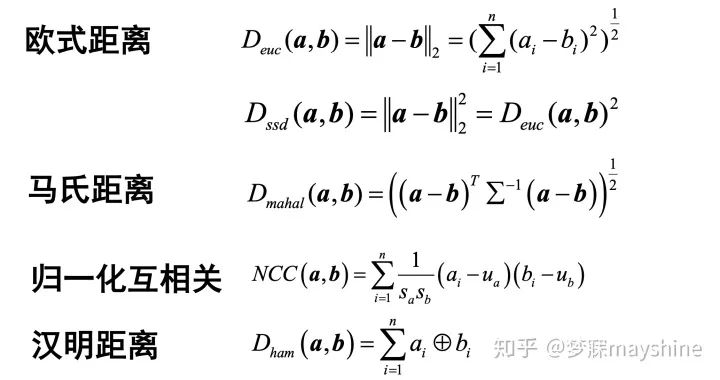
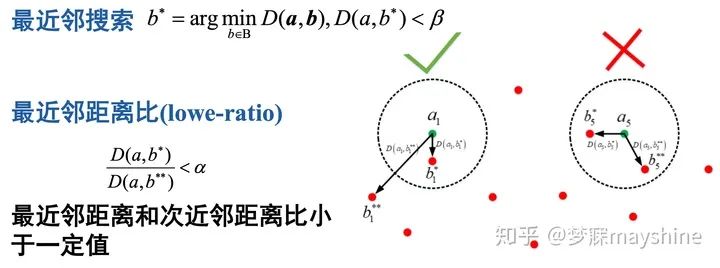
2、匹配策略
最近邻:加了距离约束,防止孤立点
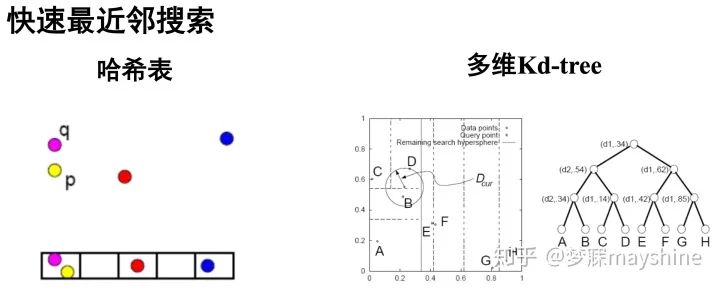
3、高效匹配
4、特征匹配验证



审核编辑 :李倩
-
机器视觉图像处理之角点检测技术2016-01-22 4314
-
特征点(角)检测与匹配2020-05-06 1642
-
Firefly RK3399Pro开源主板 + 单目摄像头,人体特征点检测方案2022-04-01 2614
-
一种基于轮廓分析的图像特征点检测方法2009-12-14 845
-
基于改进局部不变特征的兴趣点匹配2010-02-10 529
-
基于区域检测特征匹配方法设计研究2017-10-28 1034
-
FAST特征点检测features2D2017-11-29 3748
-
firefly人体特征点检测介绍2019-11-05 2118
-
基于Laplace-Beltrami算子的特征点检测算法2021-04-21 947
-
基于高斯金字塔图像的改进Harris特征点检测算法2021-05-06 1041
-
高阶多视图离群点检测及其研究综述2021-05-07 937
-
基于单位统计曲率特征匹配的红外目标检测2021-06-19 717
-
基于计算机视觉领域中的特征检测和匹配研究2023-06-16 5415
-
三种最常用的特征检测与匹配算法总结2023-06-19 8559
-
DCNN网络结构 DCNN的人脸特征点检测2023-07-20 535
全部0条评论

快来发表一下你的评论吧 !

